How To Solve Linear Equation Questions Quickly

November 17, 2019

How to Solve Linear Equation Question & Definition

A linear equation is an equation where variable quantities are in the first power only and whose graph is a straight line.
how to solve linear equation quickly

  • To solve questions quickly
    y= mx + b
 
 
Linear Equation solve question quickly and how to solve

Type 1: How To Solve Linear Equations Questions Quickly.
Find the value of x or y

Question 1.

If 3a + 7b = 75 and 5a – 5b = 25, what is the value of a + b?

Options:

  1. 11
  2. 6
  3. 5
  4. 17

Solution:

3a + 7b = 75 ……(1)
5a – 5b = 25 (divide the equation by 5)
we get, a – b = 5 …….(2)
Now multiplying eq. (2) by 7 and add to eq. (1), we get
3a + 7b = 75
7a – 7b = 35

On solving

10a = 110

a = 110/10

a = 11

Now put the value of a in eq (2)

11 – b = 5

b = 11 – 5

b = 6

Therefore, a = 11 and b = 6

The value of a + b = 6 + 11 = 17

Correct option: D

Question 2.

If 2x + y = 16 and 16x – y = 2, then find the value of x?

Options:

  1. 1/4
  2. 17/4
  3. 17/8
  4. 4

Solution:

Given, 2x + y = 16

2x + y = 24

x + y = 4….(1)

Now, 16x – y = 2

(24) x – y = 2¹

x – y = 1/4 ….(2)

On solving equation 1 and 2

We get,

2x = 17/4

x = 17/(4 * 2) = 17/8

Correct option: C

Question 3.

The system of equations 3a + 5b = 6 and 6a + 10y = 6 has

Options:

  1. No solution
  2. One solution
  3. Two solution
  4. Infinite solution

Solution:

a1/a2 = 3/6 = 1/2

b1/b2= 5/10 = 1/2

c1/c2 = 6/6 = 1

a1/a2 = b1/b2 ≠ c1/c2

Therefore, there is no solution

Correct option: A

Type 2: Solve Quickly Linear Equations Questions.
Based on Word problems

Question 1.

The difference between the two numbers is 45. The ratio of the two numbers is 8:3. Find the two numbers?

Options:

  1. 72 and 27
  2. 90 and 45
  3. 81 and 36
  4. 60 and 15

Solution:

Let the first number be 8x

Let the second number be 3x

Now, the difference between the two numbers is 45

Therefore, 8x – 3x = 45

5x = 45

x = 45/5

x = 9

Now, put the value of x in

8x = 8 * 9 = 72

3x = 3 * 9 = 27

Correct option: A

Question 2.

The breadth of a rectangle is twice its length. If the perimeter of the rectangle is 84m. Then, calculate the length and breadth of the rectangle?

Options:

  1. L=12 and B= 24
  2. L = 14 and B = 28
  3. L = 28 and B = 14
  4. L = 24 and B = 12

Solution:

Perimeter of rectangle = 2 (l+b)

Length of the rectangle = x

Breadth of the rectangle = 2x

Perimeter of the rectangle = 84

2 (x + 2x) = 84

2 (3x) = 84

6x = 84

x = 84/6

x = 14

Therefore, the Length of the rectangle = 14m

And Breadth of the rectangle = 14 * 2 = 28m

Correct option: B

Question 3.

Ajay bought 5 tickets for two concerts A and B and 10 tickets for concert A and C. He paid Rs. 350. Now the total of a ticket for concert A and B and ticket of A and C is Rs. 42, then what is the ticket price for concert A and B?

Options:         

  1. Rs. 10
  2. Rs. 42
  3. Rs. 14
  4. Rs. 28

Solution:

Let the ticket price of concert A and B = a

Let the ticket price of concert A and C = b

According to the question, a + b = 42…… (1)

Ticket bought by Ajay = 5a + 10b = 350

= a + 2b = 70……(2)

Now solve equation 1 and 2

a + b = 42

a + 2b = 70

b = 70 – 42

b = 28

Now put the value of b in equation 1

a+ 28 = 42

a = 42 – 28

a = 14

Hence, the ticket price for concert A and B = Rs. 14

Correct option: C

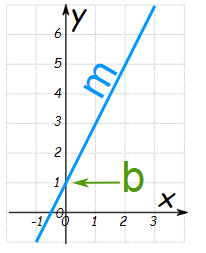
Please Login/Signup to comment