0
Notifications Mark All Read
- Login
- Get Prime
Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
Alligations and Mixture Formulas
Formulas For Alligation And Mixture
A mixture, as the name suggests is mixing two or more things together and alligation enables us to find the ratio in which the ingredients/ things have been mixed to form the mixutre.
The most fundamental point to remember while solving mixtures and alligations is that alligation is a way to find the mean value of mixture when the ratio and amount of the ingredients mixed are different and also to find the proportion in which the elements are mixed.


Formulas to Solve Alligations and Mixtures question :-
What is an Alligation?
When two ingredients X and Y of price p and q respectively are mixed together, such that the price of the resultant mixture is M (mean price), then the ratio (R) in which ingredients are mixed is given by, the rule of the alligation.
(Cheaper quantity) : (Dearer quantity) = (d – m) : (m – c)
What is a Mixture?
In a mixture, two or more ingredients are mixed together to get a desired quantity. The quantity can be expressed as ratio or percentage.
For example: When two varieties of sugar are mixed to form a new variety of sugar then it is called as a mixture.
What is a Mean Price?
The cost of a unit quantity of the mixture is called the mean price.
Formulas to Solve Mixture and Alligations
Alligation and Mixture Formulas 1
When two commodities are mixed then ,
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Alligation and Mixture Formulas 2
Consider a container contain x unit of liquid A from which y units are taken out and replaced by water. This operation is repeated n number of times, then the quantity of pure liquid will be given by the formula:
Quantity = \left[x – (1 – \left(\frac{Y}{X}\right)^n \right] units
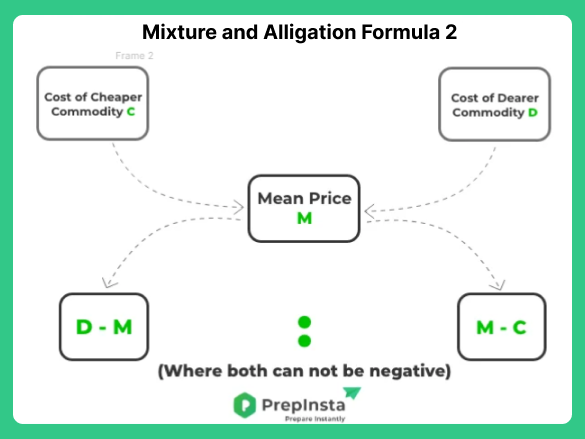
Therefore, (Cheaper Commodity) : (Dearer Commodity) = (d – m) : (m-c)
Alligation and Mixture Formulas 3
Calculate quantity of pure Liquid after ‘n’ successive operations,
If a container contains ‘x’ units of pure liquid , and we replace the liquid with ‘y’ units of water ,
Then after ‘n’ successive operations, the units of pure liquid left is ,
| After n operations, the quantity of pure liquid = |  | x |  | 1 — | y |  | n |  | units. |
| x |
Criss-Cross Method
Some aspirants use the above method in different format, which we call criss-cross method. Below is the format:
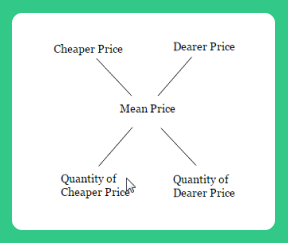
The working is, we take the positive difference of mean price and cheaper price and write the difference in the place of Quantity of dearer price. Similarly, take the positive difference of mean price and dearer price and write the difference in the place of Quantity of cheaper price.
Rule of Constant
There are another types of questions on mixtures and alligation where the quantity of one element in the mixture does not change while adding another element to the first mixture. For such questions, I recommend an alternate method of using the rule of constant to get to the answer. The concept uses the simple understanding of percentages. Let us learn it with the help of an example.
Method 1: School textbook approach
We assume that the quantity of water added to be x litres. The quantity of milk in the existing solution is 30% of 40 = 12 litres, with the addition of water, the quantity of new solution becomes (40 + x) litres. As per the problem, the percentage of milk in new solution should be 15 %. we will get x = 40.
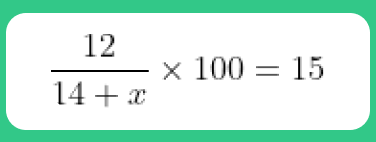
Method 2: Rule of Alligation.
We assume that the two solutions of milk and water are added to get the new solution and apply the approach we used in Example 3.
Taking milk as the common element in both the solutions, we have 30% milk in first and 0% milk in the second solution (i.e. pure water). On mixing them, we got 15% milk in the final solution. Therefore,
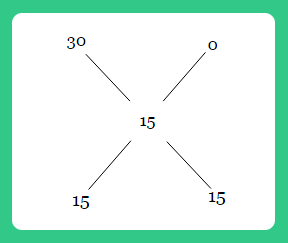
Or the ratio of the quantity of first and second solution should be 15:15 = 1:1
Hence, 40 litres of pure water should be mixed to get the desired new solution.
Method 3: Rule of Constant
In this rule, we target the element in the mixture whose amount does not change but its percentage changes because of the change in the total amount of the mixture.
As we calculated above, the quantity of milk in the first solution is 12 litres, and it will remain same in the new solution as well. That is,
12 liters = 30% of the first solution =15% of the new solution
Question 1 :
A and B are two alloys of iron and silver prepared by mixing metals in the ratio 4 : 5 and 7 : 5 respectively. If equal quantities of alloys are melted to form a third alloy C, the ratio of iron to silver in C is
Solution :
In alloy A, the ratio of iron to Silver=4:5, 5+4=9
In alloy B, the ratio of iron to Silver=7:5, 7+5=12, as the amount to be mixed.
So take the LCM of 9 and 12. hence, we mix 36 gm of A and 36 gm of B.
(the reason for choosing LCM as the amount is to simplify calculations.)
For a: amount of iron=\frac{4}{9}\times36=16 and amount of silver \frac{5}{9}\times36=20
For B: amount of iron=\frac{7}{12}\times36=21 and amount of silver=\frac{5}{12}\times36=15
Hence, Total amount of iron=16+21=37
Total amount of silver=20+15=35
Hence, Final ratio of iron to Silver in the mix of two alloys= 37:35
Question 2 :
Mixture of alcohol and water contains 35% of alcohol by volume. Then, 40 ml of water is added to such a mixture of 100 ml. The percentage of alcohol in the new mixture is?
Solution :
Question 3 :
Solution :
Question 4 :
From two ornament Weighing 18 gram and 24 gram containing gold and silver in the ratio of 2: 1 and 5: 1 respectively, a new ornament is made. What is the amount of gold in the new ornament?
Solution :
from the first ornament, gold = \frac{2}{3}\times18=12
From the second ornament gold= \frac{5}{6}\times24=20
Thus, total gold=32 gm.
Question 5 :
A sum of money is sufficient to pay Sachin’s salary of 45 days and kale’s salary for 60 days. For how many days can the sum pay the salary of both?
Solution:
Sachin’s salary for one day = 1/45th of the sum of money.
For kale’s salary for one day = 1/60 of the sum of money.
=> (Sachin + kale)’s salary for one day= 1/45+1/60=7/180th of the sum.
Hence, when they both work together, the sun will last for 180/7 days.
Also Check Out
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Averages – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Ratio and Proportions – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Simple & Compound Interest – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Simple Interest – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Compound Interest – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Percentages – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Profit & Loss – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
Others
- Averages – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Ratio and Proportions – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Simple & Compound Interest – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Simple Interest – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Compound Interest – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Percentages – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Profit & Loss – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts
Others

 0
0



Login/Signup to comment