Formulas For Inverse

March 6, 2024

Formulas for Inverse in Aptitude

Here , In this Page Formulas for Inverse is given. Inverse is a Function that Reverses another Function.

If the function is denoted by f(x) then inverse is denoted by f^{-1}(x)

Inverse functions gives lots of troubles so here’s a swift run down of what an inverse function is, and how to find it.

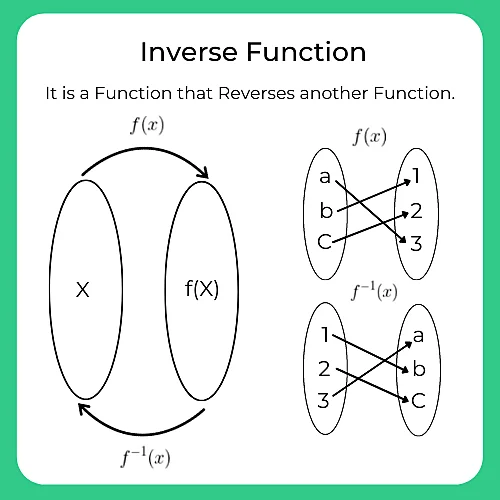
Formulas for Inverse

Types of Inverse function

FunctionInverse FunctionNote
+– 
*/Don’t divide by 0
1/x1/yx and y not equal to 0
x^{2}\sqrt{y}x and y ≥ 0
x^{n}y^{1/n}n is not equal to 0
e^{x}In(y)y > 0
a^{x}log a(y)y and a > 0
Sin xSin^{-1}(y)– π/2 to + π/2
Cos xCos^{-1}(y)0 to π
tan xtan^{-1}(y)– π/2 to + π/2

Inverse Formulas Example-

f(x) = 3x -2 and g(x) =\frac{x}{3} + \frac{2}{3}

(f∘g)(x)= (g∘f)(x) = x

  • The first case is really,

(g∘f)(−1)=g[f(−1)]=g[−5]=−1

  • The second case is really,

(f

  • A function is called one-to-one if no two values of x produce the same y. Mathematically this is the same as saying
    f(x1)\neq f(x2)  whenever x1 \neq x2
  • Inverse functions are one to one functions f(x) and g(x) if
    (f∘g)(x) = x and (g∘f)(x) = x, then we can say f(x) and g(x) are inverse to each other.
  • g(x) is inverse of f(x) and denoted by
    g(x)= f-1 (x)
  • Like wise f(x) is the inverse of g(x) are denoted by
    f(x)= g-1 (x)

For the two functions that we started off this section with we could write either of the following two sets of notation.
f(x) = 3x -2

f-1 (x) = \frac{x}{3} + \frac{2}{3}

g(x) = \frac{x}{3} + \frac{2}{3}

g-1 (x) = 3x-2

Inverse Formulas with solved Examples

Given f(x)  3x – 2 find \mathbf{f^{-1} (x)}

Solution:

we’ll first replace f(x) with y

y= 3x-2

Next, replace x with y and all y with x.
x = 3y -2
x + 2 = 3y
\frac{1}{3} (x+2) = y
\frac{x}{3} + \frac{2}{3} = y
Finally, replace y with f^{-1} (x)
f^{-1} (x) = \frac{x}{3} \ + \frac{2}{3}
f∘f^{-1} (x) = f[f^{-1}(x)]
= f[  \frac{x}{3} \ +  \frac{2}{3} \ ]
= 3 (  \frac{x}{3} \ +  \frac{2}{3} \ ) – 2
= x + 2 – 2
= x

Question and Answers for Inverse

Question 1 : Let f(x) = x^3 + 2x + 1. Find the domain of the inverse function of f(x).

A. (-\infty, \infty)
B. [-1, \infty)
C. (-\infty, -1] U [0, \infty)
D. (-\infty, -1) U [0, \infty)

Explanation:
To find the domain of the inverse function of f(x), we first need to find the inverse function of f(x) and then find the domain of the inverse function.
Since finding the inverse function is a bit complicated for a cubic function, we can use a shortcut by noticing that f(x) is an increasing function on its domain (which is (-\infty, \infty)), which means that its inverse function also has a domain of (-\infty, \infty). Therefore, the answer is (a).

Question 2 : Let f(x) = (2x – 1) / (3x + 4). Find inverse of f(x)

A. f^{-1}(x) = \frac{1+4x}{2-3x}
B. f^{-1}(x) = \frac{2-3x}{1+4x}
C. f^{-1}(x) = \frac{4x+1}{3x-2}
D. f^{-1}(x) = \frac{3x+4}{2x-1}

Solution:
To find f^{-1}(x), we switch x and y and solve for y:<br /> x =\frac{2y – 1}{3y + 4} ,
x(3y + 4) = 2y – 1,
3xy + 4x = 2y – 1,
y(2 – 3x) = 4x + 1,
y =\frac{4x + 1}{2 – 3x} ,
Therefore, f^{-1}(x) = (4x + 1) / (2 – 3x)

Question 3 : Let f(x) = 3x – 1. Find the inverse function of f(x).

A. f^{-1}(x) = (x + 1)/3
B. f^{-1}(x) = (x – 1)/3
C. f^{-1}(x) = (x – 1)*3
D. f^{-1}(x) = (x + 1)*3

Explanation:
To find the inverse function of f(x),
we need to solve for x in terms of f(x) and then interchange x and f(x).
So, we start with y = 3x – 1, then solve for x as x = (y + 1)/3.
Next, we replace x with f^{-1}(x) and y with x in the equation to get
f^{-1}(x) = (x + 1)/3

Question 4 : Let f(x) = 3x + 2. Find inverse of this function

A. (x – 2) / 3
B. (x + 2) / 3
C. (x – 3) / 2
D. (x + 3) / 2

Solution:
To find the inverse of f(x), we switch x and y and solve for y:
x = 3y + 2,
x – 2 = 3y,
y = (x – 2) / 3.
Therefore, Inverse of f(x) = (x – 2) / 3.

Question 5 : Let f(x) = 2x – 5. Find f^{-1}(x).

A. f^{-1}(x) = \frac{x}{2} – 5
B. f^{-1}(x) = \frac{x+5}{2}
C. f^{-1}(x) = \frac{2}{x} – 5
D. f^{-1}(x) = \frac{x-5}{2}

Solution:
To find f^{-1}(x), we switch x and y and solve for y:
x = 2y – 5,
x + 5 = 2y,
y = (x + 5) / 2.
Therefore, f^{-1}(x) = \frac{x+5}{2}

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Also Check Out

Questions and Answers to solve Inverse
How to solve Inverse Questions quickly
Tips, Tricks and shortcuts for Inverse
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout