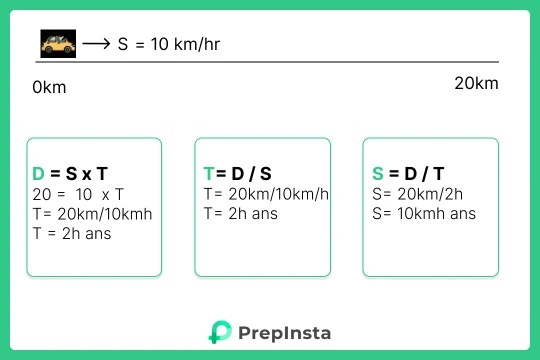
Speed Time and Distance Formulas

September 22, 2023

Basic Formulas of Speed, Distance and Time with Definition

On this page we have discussed about Speed Time and Distance formulas with Examples.

Speed Speed can be defined as the rate at which an object covers distance in a specific direction within a given timeframe.

Distance Distance can be defined as a scalar quantity that represents the numerical measure of the extent between two points in space.

Time Time can be defined as the continuous and irreversible progression of events and existence and is typically measured in units like seconds(s), minutes(mins) and hours(hr).

Formulas of Train for Speed, Distance and Time

Train problems are very common problems which are asked in quantitative aptitude exams of companies, apart from basic speed distance and time questions hence students must focus on trains problems.

Here we have discussed some basic formulas required for train problems that are asked in exams

Speed of the Train = $\frac{Total Distance}{Total Time Taken}$
If length of two trains is given, say t1 and t2, and the trains are moving in opposite directions with speeds of x1 and y1 respectively, then the time taken by trains to cross each other = $\frac{T1 + T2}{X1 + Y1}$
If the length of two trains is given, say t1 and t2, and they are moving in the same direction, with speeds x1 and y1 respectively, then the time is taken to cross each other = {(t1+t2) / (x1-y1)}
When the start time of two trains is the same from position a and b towards each other and after crossing each other, they took t1 and t2 time in reaching a and b respectively, then the ratio between the speed of trains is = $\frac{\sqrt{T2}}{\sqrt{T1}}$
If two trains leave station a and b at time t1 and t2 respectively and travel with speed X and Y respectively, then distanced from x, where two trains meet is = $\frac{(T2-T1)\times (X\times Y)}{(X1-Y1)}$
The average speed of a train without any stoppage is x1, and with the stoppage, it covers the same distance at an average speed of y1, then Rest Time per hour = (Difference in average speed) / (Speed without stoppage)

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Also Check Out

Question and Answers on Speed Distance and Time

Q1. Arnold bane travels from one place to another at 60 km/hr and returns at 240 km/hr. If the total time taken is 5 hours, then find the Distance.

Options: A)120km
B)360km
C)280km
D)240km

Answer :
Here the Distance is constant, so the Time taken will be inversely proportional to the Speed. Ratio of Speed is given as 60:240, i.e. 1:4
So the ratio of Time taken will be 4:1.
Total Time taken = 5 hours; Time taken while going is 4 hours and returning is 1 hour.
Hence, Distance = 60x 4 = 240 km
Option D is correct

Q2.Anthony Milan by bus takes double the Time taken by train to travel from Bangalore to Chennai. What is
the Speed of the train if the Speed of the bus is 95 km/hr.

Options: A)60km
B)50km
C)180km
D)190km

Answer:
Let’s denote the speed of the train as “x” km/hr, Tb time taken by bus, Tt time taken by train, Sb speed of bus
The time taken by the bus to travel from Bangalore to Chennai is given by:
Tb = Distance / Sb
Since the speed of the bus is 40 km/hr, we can rewrite the equation as:
Tb = Distance / 95
According to the given information, the time taken by the bus is double the time taken by the train:
Tb = 2 * Tt
Substituting the expressions for Tb and Tt, we get:
Distance / 95 = 2 * Distance / x
To solve for the speed of the train (x), we can cross-multiply and solve for x:
Distance * x = 95 * 2 * Distance
x = 190 km/hr
Option D is correct.

Q3. Train X can travel 50% faster than a car Y. Both start from New Delhi at the same time and reach Meerut which is 75 kms away from New Delhi at the same time. However, the train lost about 12.5 minutes while stopping at the stations. The speed of the car Y is:

Options: A)120km
B)300km
C)160km
D)240km

Answer: Let the speed of car be x km

Then the speed of Train = $\frac{150}{100}x$
= $\frac{3}{2}x$
$\frac{75}{x}-\frac{75}{\frac{3}{2}}x = \frac{125}{10 \times 60}$
$\frac{75}{x}-\frac{50}{x} =\frac{5}{24}$
$x = \left (\frac{25\times 24}{5} \right )$
120 km/hr
Option A is correct.

Q4.A train travels from Station A to Station B at a constant speed of 80 km/h. On its return journey from Station B to Station A, the train encounters some technical issues, and its speed reduces to 60 km/h. The total time taken for the whole trip is 9 hours. Find the distance between Station A and Station B.

Options: A)308.57 km
B)156.4 km
C)200 km
D)123.7 km

Answer:

Let the distance between Station A and Station B be D kilometers. Time taken for the journey from A to B: D / 80 hours Time taken for the journey from B to A: D / 60 hours
According to the problem, the total time taken for the round trip is 9 hours. So we can set up the equation: D / 80 + D / 60 = 9
To solve for D, we can find the least common multiple (LCM) of 80 and 60, which is 240. Then, we get: (3D + 4D) / 240 = 9 7D = 9 * 240 D = 9 * 240 / 7 D ≈ 308.57 km
Therefore, the distance between Station A and Station B is approximately 308.57 kilometers
Option A is correct.

Q5. A high-speed train departs from City P to City Q at 8:00 AM. At the same time, another train leaves City Q and travels towards City P at a speed of 120 km/h. The distance between the two cities is 480 kilometers. If the high-speed train travels at a constant speed of 180 km/h, at what time will the two trains pass each other?

Options: A)9:30 am
B)4:30 am
C)12:40 pm
D)8:00 am

Answer:

Let the time at which the two trains pass each other be T hours after 8:00 AM.
Distance covered by the high-speed train = 180 km/h * T hours Distance covered by the other train = 120 km/h * T hours
According to the problem, the total distance between the cities is 480 kilometers.
So, we can set up the equation: 180T + 120T = 480
300T = 480 T = 480 / 300 T = 1.6 hours
The two trains will pass each other 1.6 hours after 8:00 AM.
Option D is correct.