How To Solve LCM Questions Quickly

March 6, 2024

Solve LCM Problems Quickly and Easily

On this page you will found about, How to solve LCM Questions Quickly with the help of formulas and tricks. You will also get to know about the basic concepts of LCM along with different method to solve LCM Questions.

how to solve problems on lcm

How to Solve LCM Questions Quickly

  • LCM – The least number which is exactly divisible by each one of the given numbers is called their L.C.M.
  • The least common multiple (LCM) of two or more positive integers is the smallest integer which is a multiple of all of them. Any finite set of integers has an infinite number of common multiples, but only one LCM. The LCM of a set of numbers $\{a_1,a_2,\cdots,a_n\}$ is conventionally represented as $[a_1,a_2,\ldots,a_n]$.

Factorization Method:

Resolve each one of the given numbers into a product of prime factors. Then, L.C.M. is the product of the highest powers of all the factors.

Example : Find out LCM of 8 and 14

Express each number as a product of prime factors. (Reference: Prime Factorization)

8 = 2 × 2 × 2

14 = 2 × 7

 LCM = The product of highest powers of all prime factors.

Here the prime factors are 2 and 7

The highest power of 2 here = 3

The highest power of 7 here = 1

Hence LCM = 2× 2× 2 × 7 = 56

Division Method (short-cut):

Arrange the given numbers in a row in any order. Divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible. Repeat the above process till no two of the numbers are divisible by the same number except 1. The product of the divisors and the undivided numbers is the required L.C.M. of the given numbers.

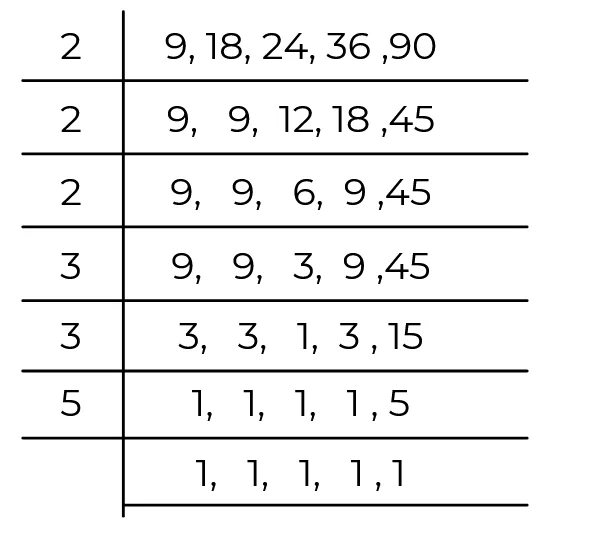
Example 2: Find out LCM of 18, 24, 9, 36 and 90

How To Solve LCM Questions Quickly

Hence Least common multiple (L.C.M) of 18, 24, 9, 36 and 90

= 2 × 2 × 2 × 3 × 3 × 5

= 360

LCM of 18, 24, 9, 36 and 90 is 360.

Type 1: How To Solve LCM Questions Quickly. Find the least or greatest number

Question 1. What will be the least number which when doubled will be exactly divisible by 12, 14, 16, 18, and 22?

Options

A. 630

B. 5544

C. 4544

D. 2534

Solution  :    L.C.M. of 12, 14, 16, 18, and 22 = 11088

Required number = (11088 ÷ 2) = 5544

Correct option:B

Question 2 : The least number which when divided by 13, 17 and 19 leaves a remainder 10 in each case is?

Options

A. 4209

B. 4290

C. 4029

D. 4902

Solution :   Required number = (L.C.M of 13, 17, 19) + 10 = 4199 + 10 = 4209

Correct option:A

Question 3 : The L.C.M. of two numbers is 40. The numbers are in the ratio 2: 5. Find the sum of the number both the numbers?

Options

A. 26

B. 25

C. 28

D. 120

Solution   :   Let the numbers be 2x and 5x.

Then, their L.C.M. = 10x

So, 10x = 40 or x = 4

Numbers are 2x = 2 * 4 = 8

5x = 5 * 4 = 20

Therefore, required sum = (8 + 20) = 28

Correct option:C

Type 2: How To Solve Quickly LCM Questions. Find LCM

Question 1 : Find the LCM of 16 and 28

Options

A. 121

B. 112

C. 211

D. 120

Solution :     Prime factorization of 16 = 2 * 2 * 2 * 2 = 24

Prime factorization of 28 = 2 * 2 * 7 = 22 * 71

Highest exponent value we take 24 * 71 = 112

Therefore, LCM (16, 28) = 112

Correct option:B

Question 2 : Find the L.C.M of 0.16, 5.4 and 0. 0068

Options

A. 734.4

B. 7344

C. 73.44

D. 7.34

Solution   :  L.C.M (16, 54, 68) = 7344

In numbers 0.16, 5.4, and 0.0098, the minimum digits from right to left are 5.4. Therefore, we

put decimal in our result as 734.4.

Correct option:A

Question 3 : Find the LCM of two numbers, if the ratio of two numbers is 2: 3 and their HCF is 6.

Options

A. 30

B. 18

C. 40

D. 36

Solution   :  Let the numbers be 2x and 3x

In the question, H.C.F is given as 6

Therefore, the value of x = 6

So the numbers are 2x = 2 * 6 = 12

3x = 3 * 6 = 18

L.C.M. (12, 18) = 36

Correct option:D

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Also Check Out 

Rules and Formulas to solve LCM Questions
Questions and Answers to solve LCM
Tips, Tricks and shortcuts for LCM
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout