0
Notifications Mark All Read
- Login
- Get Prime
Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
Tips And Tricks And Shortcut For Venn Diagrams
Tips and Tricks for Venn Diagrams
Venn Diagrams are a schematic and identical way of representing the elements of a set or a group. In mathematical language, it represents the intersection of the two groups. So accordingly, Venn Diagrams are quite important in both quantitative and logical reasoning. Therefore, it is important to practice Venn Diagrams Questions along with the Tips and Tricks for Venn Diagrams.

For example – A contains all the people that like cake. Set B represents all the people who like ice cake and set C represents all the people who like chips. Then the region marked as AB represents all the people who like both cake and ice cake. The region marked BC represents all the people who like both ice cake and chips. Similarly, the region AC represents all the people who like cake and ice cake.

Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
If there are only two elements
n ( A ∪ B) = n(A ) + n ( B ) – n ( A∩ B)
If there are three elements
n (A ∪ B ∪ C) = n(A ) + n ( B ) + n (C) – n ( A ∩ B) – n ( B ∩ C) – n ( C ∩ A) + n (A ∩ B ∩ C)
Question 1
In a class of 260 seniors, 93 study Spanish, 95 study Chemistry, 165 study Mathematics, 18 study Spanish and Chemistry, 75 study Chemistry and Math, 20 study Math and Spanish and 15 study all three subjects. Make a Venn diagram to illustrate the data and then find the probability that a student selected at random studies Spanish but not Maths.
Options
(a) 0.121
(b) 0.0192
(c) 0.269
(d)0.387
Correct Option (A)
Explanations
- Spanish but not Maths and Chemistry
P(S∩M’∩C’) = \frac{70}{260} = \frac{7}{26} = 0.269
- Maths and Chemistry but not Spanish
P(M∩C∩S′)= \frac{60}{230} = \frac{3}{13} = 0.231
- None of these subject
P(M′∩C′∩S′) = \frac{5}{260} = \frac{1}{52}
- Spanish, given that he/she studies Math
P(S, M)\frac{P(S\cap M')}{P(M)} = \frac{\frac{20}{260}}{\frac{165}{260}} = 0.121
Question 2
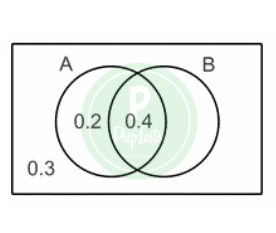
Given P(A∩B) = 0.4, P(A∩B’) = 0.2 and P(A’∩B’) = 0.3, find P(B) and P(A|B).
Options
(a) 0.8
(b) 0.6
(c) 0.4
(d) 0.2
Correct Options (A)
Explanations
The missing value, P(B∩A’), must be 0.1 in the order for the total of the probabilities in the sample space equal to 1. Thus , P(B) = 0.5
P \frac{A}{B} = \frac{P(A∩B)}{P(B)} \ = \frac{P(0.4)}{P(0.5)} \ = 0.8
Also Check Out
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Geometry – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Heights and Distances – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Perimeter Area and Volume – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Coordinate Geometry – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Set Theory – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Geometry – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Heights and Distances – Questions |
Formulas | - How to Solve Quickly |
Tricks & Shortcuts - Perimeter Area and Volume – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Coordinate Geometry – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Set Theory – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

 0
0




Login/Signup to comment