Tips Tricks And Shortcuts For Geometry

July 28, 2023

Geometry Tips and Tricks and Shortcuts

To solve questions effectively and accurately in placement exams you need to have a stronghold on the tips, tricks and shortcuts of that chapter. This page will provide you with all possible Tips Tricks and Shortcuts of Geometry questions types which are frequently asked in the exams.

The Tips Tricks of Coordinate Geometry and Shortcuts are listed below with the sample questions.

Tips Tricks and Shortcuts For Geometry

From a given perimeter how many triangles with integral sides are possible?

We can solve this manually. But with the help of a tips and tricks and shortcut that is discussed in this page of PrepInsta

  • We can solve this question within seconds. Generally there are two cases for these type of questions.

Scenario 1:

When Perimeter is odd

Scenario 2:

When perimeter is even

Scenario 1 – Details

  • How many triangles with integral sides are possible for perimeter P where P is even

Solution – In this case, total number of triangles will be the nearest integer to \frac{P^2}{48} \

Scenario 2 – Details

  • How many triangles with integral sides are possible for perimeter P where P is odd

Solution – In this case, total number of triangles will be the nearest integer to \frac{(P+3)^2}{48} \

Tips and Tricks on Geometry

Question 1:

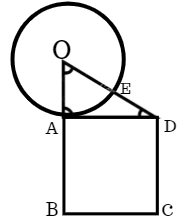
ABCD is a square. AD is tangent to circle with radius r and OE = ED. Then what is the ratio of the area of circle to the area of square?

tricks and tips and shortcuts on geometry

Options
a) \frac{Π}{3} \

b) \frac{Πr^2}{3} \

c) \frac{Πr^2}{4} \

d) \frac{2Πr}{4r} \

Explanations

OD2 = OA2+ AD2

(2r)2 = r2 + AD2

Thus PQ, which is also the side of square, is equal to r√3. The area of square becomes:  3r2
Hence the ratio of the area of circle to square is:

\frac{area  of circle}{area  of square} \ = \frac{πr^2}{3r^2} \ = \frac{π}{3} \

Correct Option (A)

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Geometry Shortcuts Tips and Tricks and Shortcuts

Question 2

If in a triangle ABC, \frac{cos A}{a} \ = \frac{cos B}{b} \ = \frac{cos c}{c} \ , then what can be said about the triangle ?

Options
A) Right angled triangle
B) Isosceles triangle
C) Equilateral triangle
D) Nothing can be inferred

Explanations

From the sine rule of triangle we know, \frac{a}{sinA} \ = \frac{b}{sinB} \ =  \frac{c}{sinC} \ = k

Therefore, a = k(sin A), b = k(Sin B) and c = k(Sin C)

Hence, we can rewrite, \frac{cos A}{a} \ = \frac{cos B}{b} \ = \frac{cos C}{c} \ as \frac{cos A}{k Sin A} \ = \frac{cos A}{k Sin B} \ = \frac{cos C}{k Sin C} \

or Cot A= Cot B= Cot C
A = B = C, Hence the triangle is equal.

Correct Option (C)

Also Check Out

Geometry question and answers for placement
How to solve geometry questions quickly?
Important Formulas related to Geometry Problems
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout