0
Notifications Mark All Read
- Login
- Get Prime
Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
How To Solve Algebra Questions Quickly
How To Solve Quickly Algebra Questions
To solve algebra questions quickly, start by mastering the essential algebraic concepts, such as equations, simplification, and factoring. Regular practice with various problem types will boost your speed and confidence. Look for patterns and use mental math tricks to simplify calculations.

Points to keep in mind while solving Algebra Questions :
Solving algebra questions quickly requires a combination of strategies and techniques. Here are some tips to help you solve algebra questions efficiently:
Understand the Question: Read the question carefully to understand what is being asked. Identify the unknown variables and the relationships given in the problem.
Write Down Given Information: Organize the information provided in the question. Write down the given equations, inequalities, or expressions.
Simplify: If the expressions are complex, try to simplify them before proceeding with calculations. Use algebraic rules and properties to simplify equations and expressions.
Use Shortcut Techniques: Learn shortcut techniques like factoring, completing the square, difference of squares, etc., to quickly simplify expressions or solve equations.
Apply Algebraic Rules: Be familiar with algebraic rules, such as the distributive property, associative property, and commutative property, to manipulate equations effectively.
Use the Right Formula: For specific algebraic problems, use appropriate formulas. For example, for finding the slope of a line, use the slope formula ( m = \frac{(y2-y1)}{(x2-x1)}).
Eliminate Wrong Answer Choices: In multiple-choice questions, if you are unsure about the correct answer, try eliminating options that are clearly incorrect. This narrows down your choices and improves your chances of selecting the right answer.
Practice Regularly: Practice a variety of algebra problems regularly to improve your speed and accuracy. The more you practice, the more familiar you become with various types of questions and strategies.
Remember, speed comes with practice and familiarity with different algebraic concepts. With regular practice and the right techniques, you’ll become more efficient in solving algebra questions quickly.

Steps to Solve Equations with one variable:
Step 1: Write down the question.

Step 2: Decide what to use to isolate the variable term.

Step 3: Eliminate the constant part using addition or subtraction method.
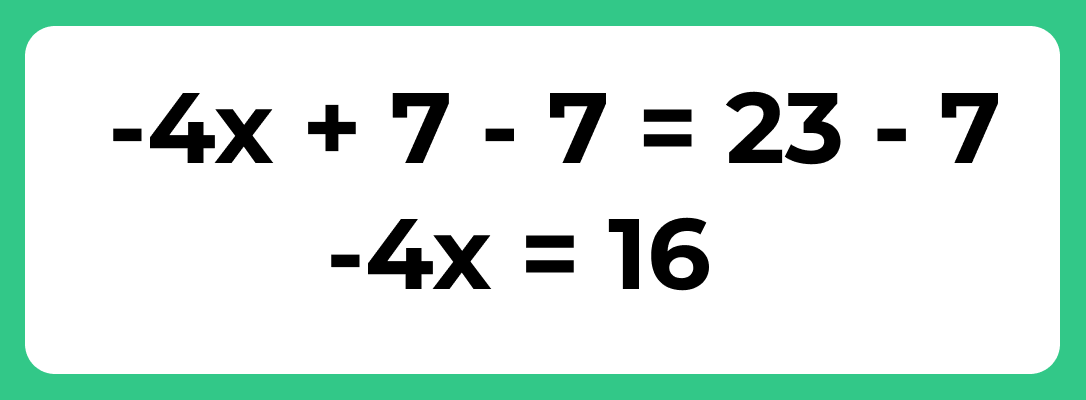
Step 4: Eliminate the coefficient of variable part.

Step 5: Solve for variable and get the answer.

Type 1: How To Solve Algebra Questions Quickly by Evaluation or finding the value of “a” variable
Question 1:
Solve the given equation 17 x – 42 + 10= 100
Options
A. 7.76
B. 15.36
C. 36.96
D. None of the above
Correct Answer: A
Explanation:
17 x – 42 + 10= 100
17x – 32 =100
17x = 100 +32
17x = 132
X= 7.76
Question 2:
Solve 6a (2 – 3) – 3 (2a + b) = 5
Options
A. 6a + 2b+7
B. 10a+ 3b
C. 12a +3b + 5
D. None of the above
Correct Answer: A
Explanation:
6a (2 – 3) – 3 (2a + b)= 5
12a – 18a – 6a -3b = 5
-6a – 6a -3b = 5
-12a – 3b = 5
12a +3b + 5
Question 3:
Find the value of x in 3 (x- 5) – 5 (2x + 9) =10
Options
A. -5.69
B. – 9.28
C. 9.28
D. None of the above
Correct Answer: B
Explanation:
3 (x- 5) – 5 (2x + 9) =10
3x – 15 – 10 x – 45 = 10
-7x – 60 = 10
-7x = 70
X= – 70/7
X= – 10
Type 2: How to Solve Algebra Questions Quickly by- Substitution Methods
Question 4:
Determine the value of 3(x)2 + 4(x)3 where x = 2
Options
A. 36
B. 56
C. 100
D. None of the above
Correct Answer: A
Explanation:
3×2 + 4×3
Substituting the value of x, we get
3(2)2 + 4(2)3
3 x 4 + 4 x 6
12 + 24
36
Question 5:
Calculate the value of the expression 3a + 2b – 15 where the value of a = 2 and b = 5.
Options
A. 6
B. 20
C. 5
D. 1
Correct Answer: D
Explanation:
3a + 2b – 15
3 * 2 + 2 * 5 -15
6 + 10 -15
1
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Linear Equations – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Quadratic Equations – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Linear Equations –
Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Quadratic Equations –
Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts

 0
0


