Formulas For Perimeter Area Volume

March 7, 2024

Perimeter, Area and Volume formulas

In this page we are going to learn about various Formulas for Perimeter Area and Volume of various geometrical shapes and figures. For your knowledge a perimeter is the path that surrounds or encompasses  a two-dimensional shape.

Formulas For Perimeter Area Volume

Perimeter, Area and Volume formulas for various shapes:-

  • Geometry is a branch of mathematics that deals with different shapes and sizes. It can be divided into two different types: Plane Geometry and Solid Geometry
  • Plane Geometry deals with shapes such as circles, triangles, rectangles, square.
  • Solid Geometry is concerned in calculating the length, perimeter, area and volume of various geometric figures and shapes. Here are some basic formulas which can be used to calculate the length, area, volume, and perimeter of various shapes and figures.

Formulas For Perimeter Area Volume:-

  • Formulas for Square

Here, s = side

    • Perimeter: 4 * s
    • Area: S2
    • Diagonal: s\sqrt{2}
    • Area of square when diagonal is given = \frac{1}{2}\times d^{2}
Formulas for Square
  • Formulas for Rectangle

Here , l = length, b = breadth.

    • Perimeter: 2 (l + b) (l = length, b = breadth)
    • Area: l × b
    • Diameter:\sqrt{l^2 + b^2 }
    • Area of 4 walls of a room = 2 (Length + Breadth) × Height
Formulas for Area (Rectangle)
  • Formulas of Circle
    • Area of circle = πr²
    • Area of semi-circle= \frac{πr^2}{2}
    • Circumference of a circle = 2πr
    • Circumference of a semi-circle = πr
    • Length of arc =\frac{2πrɵ}{360}
    • Area of sector = 1/2 (arc*R) = πr²ɵ/360
Formula for Circle
  • Parallelogram formulas
    • Perimeter: 2(a + b)
    • Area: b × h
    • Height of parallelogram = \frac{A}{b}
Formulas for Perimeter (Parallelogram)
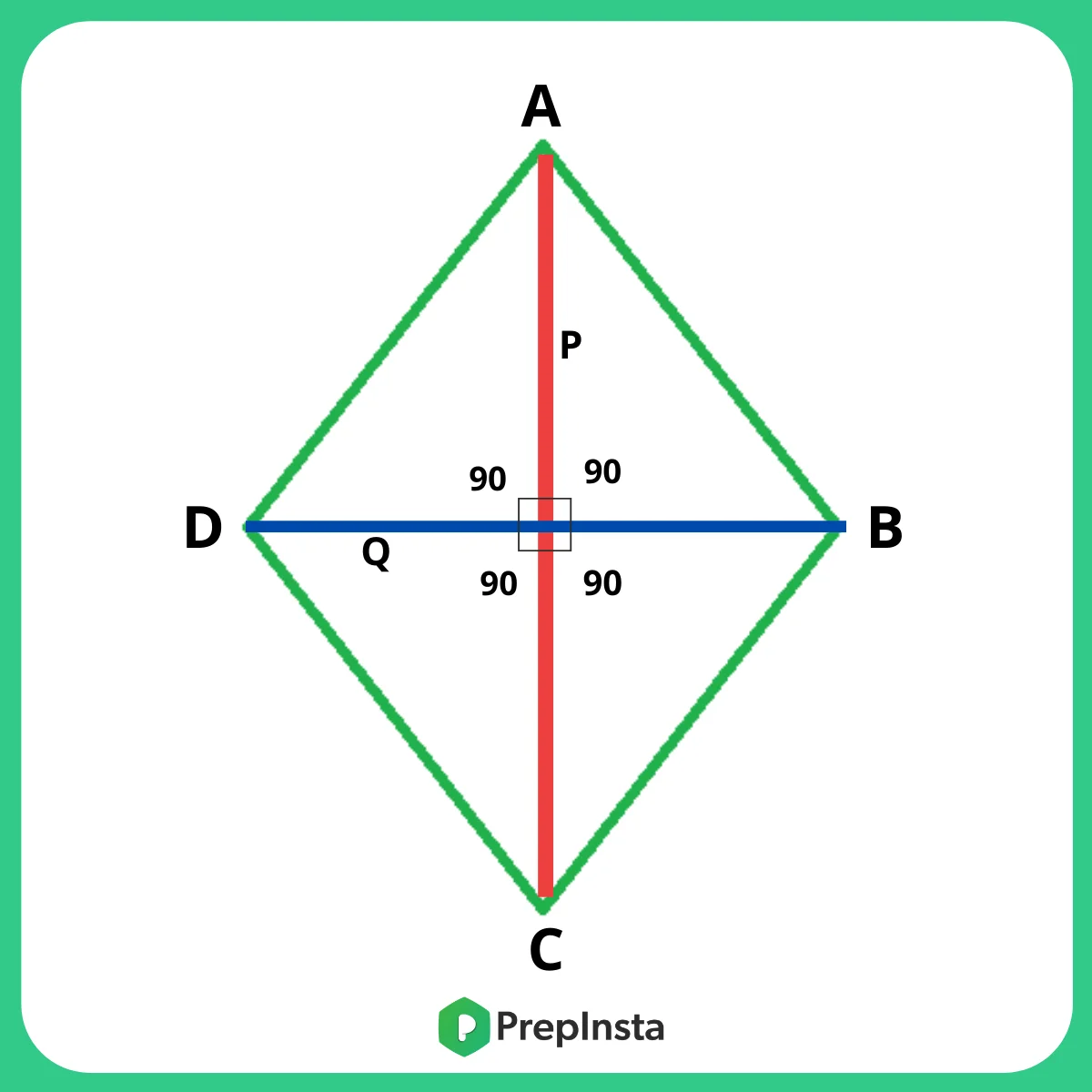
  • Rhombus formulas
    • Perimeter: 4 × a
    • Area: \frac{p\times q}{2}
    • Diagonals
      p = p = \sqrt{4a^{2} – q^{2}}
      q = p = \sqrt{4a^{2} – q^{2}}
Formula for Rhombus
  • Trapezium formulas
    • Perimeter: a + b + c + d
    • Area: \frac{1}{2} × (sum of parallel sides) × distance between them
    • To find thee distance between parallel sides you will have to convert trapezium to rectangle and then use PYTHAGORAS THEOREM.
Formulas for Area (Trapezium)
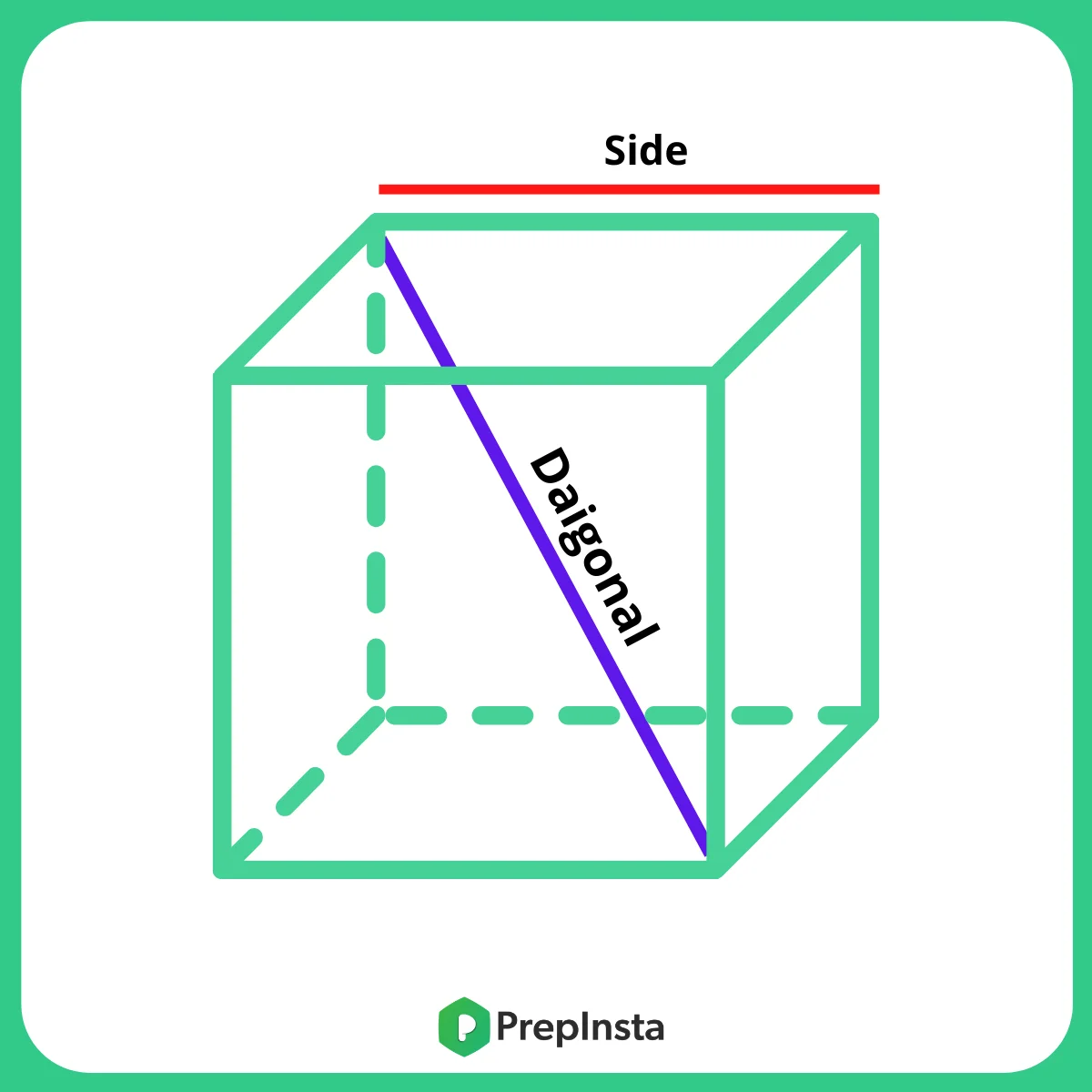
  • Cube formulas
    • Volume: (side)³
    • Surface area = 6s²
    • Partial Surface area = 4s2
    • Diagonal = \sqrt{3}s
Formula for Cube
  • Cuboid formulas
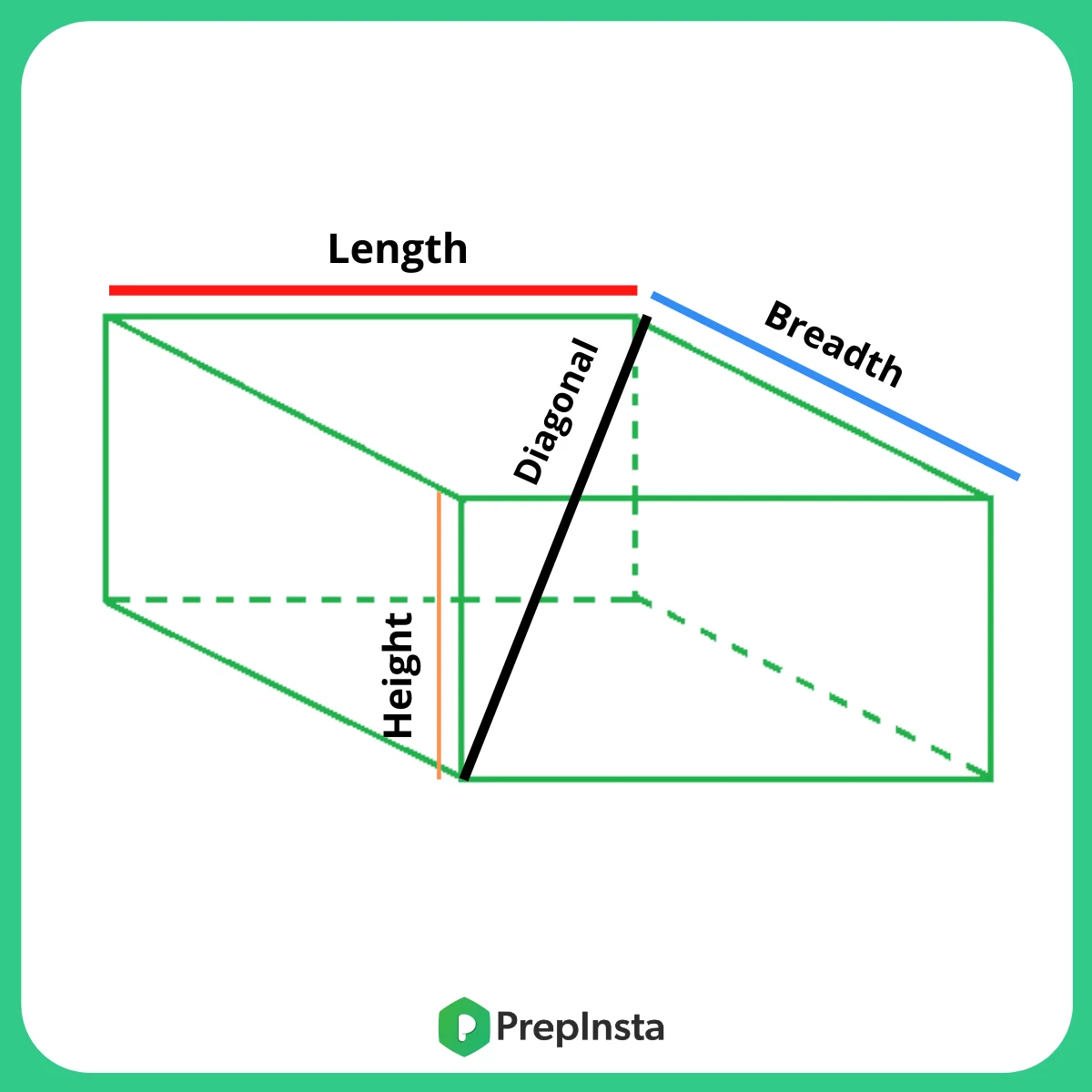
    • Volume: l * b * h
    • Surface area = 2 (lb + bh + hl)
    • Curved Surface area = 2h(l+b)
    • Diagonal = \sqrt{l^2 + b^2 + h^2}
Formulas for Volume (Cuboid)
  • Sphere formulas
  • Formulas for Sphere
    • Volume: \frac{4}{3}πr³
    • Surface area = 4πr²
Formula for Sphere
  • Hemisphere formulas
    • Volume: \frac{2}{3}πr³
    • Curved Surface area = 2πr²
    • Total Surface area = 3πr²
Formulas for Volume (Hemisphere)
  • Cylinder formulas
    • Volume: πr²h
    • Curved Surface area = 2πrh
    • Total Surface area = 2πr (h + r)
Formula for Cylinder
  • Cone formulas
    • Volume: \frac{1}{3}πr²h
    • Slant height = l = \sqrt{h^2 + r^2 }
    • Curved Surface area = πrl
    • Total Surface area = πrl +πr
Formulas for Surface Area and Volume (Cone)

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Some Examples Based On Above Formulas

Question 1: Rohan Bought a House, which had a garden outside it, with sides measuring 12 meters and 8 meters, Find the perimeter of the  garden ? 

Answer: The formula to find Perimeter is , P= 2(L+W)
= 2(12+8)
=2(20)
=40m Ans.

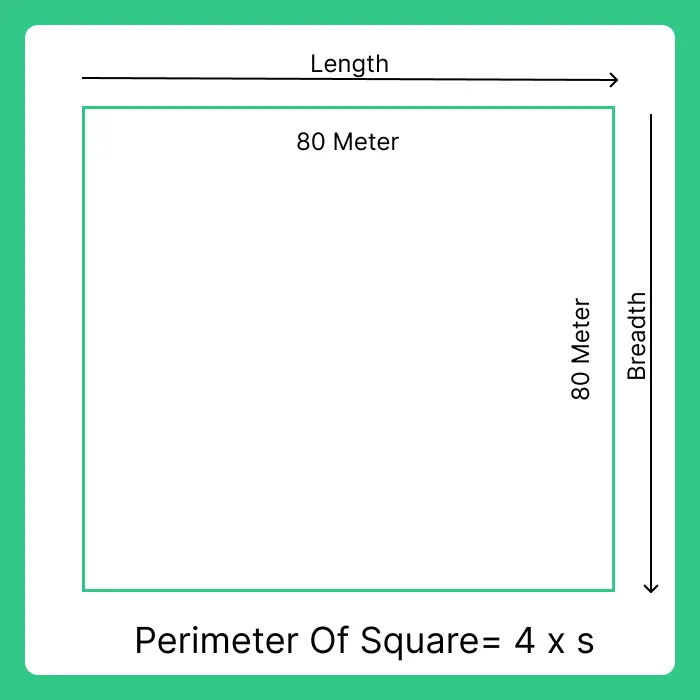
perimeter and area formula

Question 2:To protect his house from Robbers, Mohan wrapped a wire around his square plot. If the wire’s length is 80 meters, what is the perimeter of the square?

Answer: Perimeter of Square Plot = 4a(Where a = length of side)
= 4 x 80
= 320m Ans.

perimeter and area formula

Question 3: Two kids planned to make an equilateral traingle  of a cardboard , The length of one side of  the traingle being  8 centimeters. Calculate the perimeter of the triangle.

 Answer: Perimeter  of Equilateral Traingle = 3 x Side length
= 3 x 8
= 24m Ans

perimeter area formula

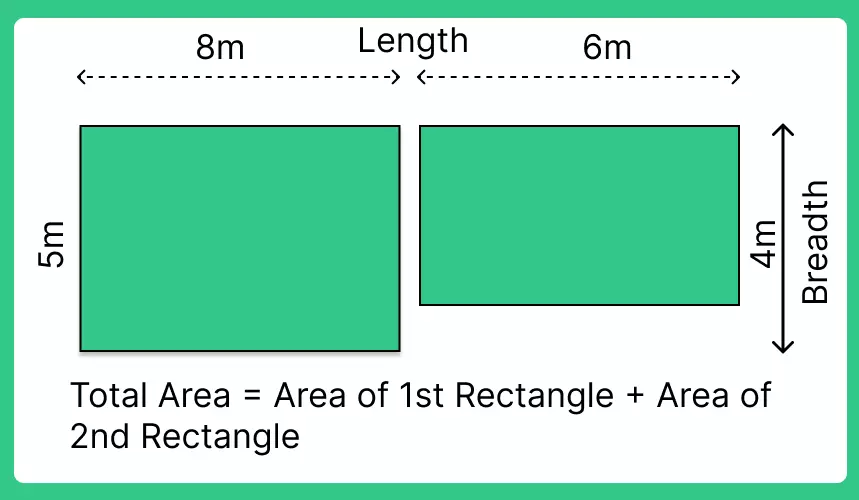
Question 4: Rahul Came up with an idea to make figure made up of two adjacent rectangles, one measuring 8 meters by 5 meters and the other 6 meters by 4 meters. Find the total area of the figure.

Answer: Total area of the figure = Area of the first rectangle + Area of the second rectangle
 = (8 meters × 5 meters) + (6 meters × 4 meters)
= 40 square meters + 24 square meters
= 64 square meters.

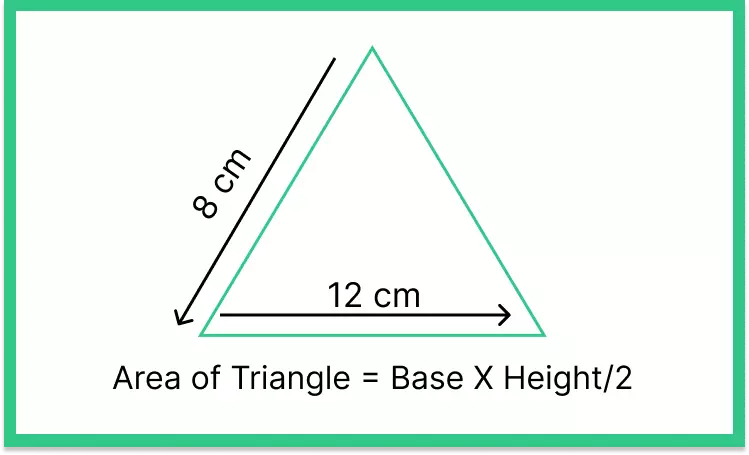
Perimeter and area Formulas

Question 5: The base of a triangle measures 12 centimeters, and its height is 8 centimeters. Find the area of the triangle.

Answer: Area of the triangle = (Base × Height) / 2
= (12 centimeters × 8 centimeters) / 2
= 48 square centimeters.

perimeter and area

Also Check Out

Perimeter Area and Volume Question and Answer
Tips Tricks and Shortcut for Perimeter Area and Volume
How to solve Perimeter Area and Volume Quickly?
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout