Tips and Tricks and Shortcuts To Solve Cube questions

August 18, 2023

Tips and Tricks and Shortcuts for Cube:-

In this Page Tips and Tricks to Solve Cube Questions is given.

Definition A cube is a three-dimensional shape, which has six equal squares. A Cube and dice have total of 6 faces, 8 vertices, and 12 edges. The 3 visible sides of cube at the same time can never be on the opposite side of each other.

Note : The topic of "cubes" in logical reasoning often refers to a type of visual reasoning question. It involves mentally rotating a 3D cube or set of cubes in different ways to understand how the cube(s) would appear from different angles or after certain operations.

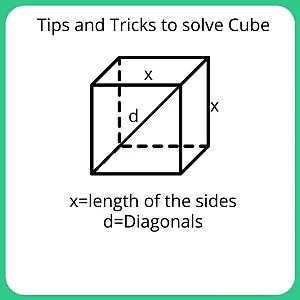
Direction for Tips and Tricks and Shortcuts for Cubes

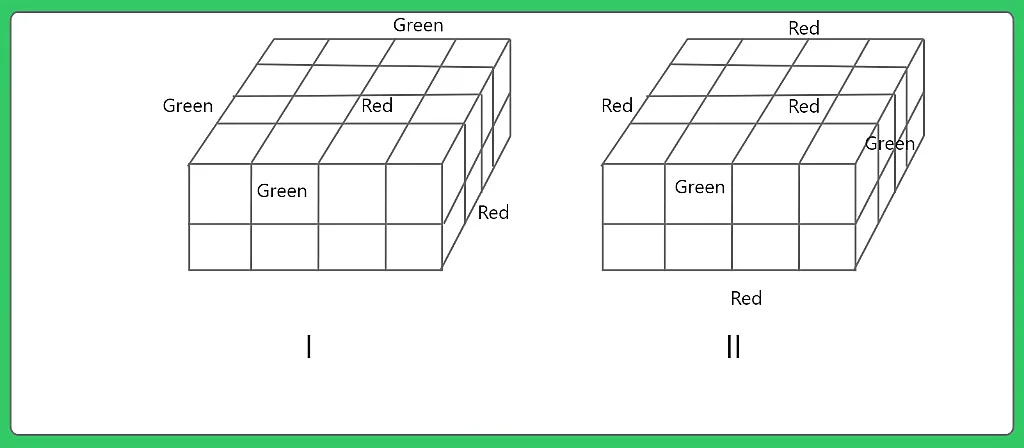
A cube is cut in two equal parts along a plane parallel to one of its faces. One piece is then colored red on the two larger faces and green on the remaining, while the other is colored green on two smaller adjacent faces and red on the remaining. Each is then cut into 32 cubes of the same size and mixed up.

Tips and tricks to solve Rubik’s Cube

Get a quality Rubik’s Cube. The solving time depends on two things: you, and the cube. Let’s focus on the other one: A Hard turning cube that stuck all the time will dramatically increase your solving time.

In a cube the number of unit cubes = (side)3.
The opposite sides of the cube can never be adjacent to each other.
If two cubes are considered, and one of the two common faces is in the same position, then the remaining faces will be opposite to each other.

Question 1: How many cubes have only one coloured face each ?

Options

A) 32
B) 8
C) 16
D) 0

Answer: Options (B)

Explanation:

8 from (I) and 8 from (II)

Therefore 8 from each.

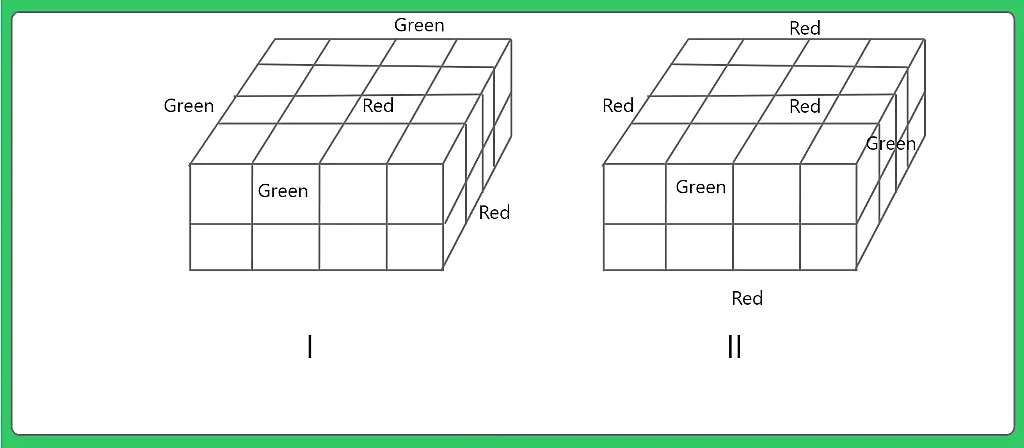
Question 2: How many cubes have each one red and another green?

Options

A) 0
B) 32
C) 16
D) 8

Answer: Option (D)

Explanation: 16 from (I) and 8 from (II)

Question 3 : A cube is coloured red on all faces.It is cut into 64 smaer cubes of equal size.How many cubes have no face coloured?

Options

A) 8
B) 16
C) 32
D) 64

Answer: Option(A)

Explanation: Since there are 64 smaller cubes of equal size,therefore n=number of divisions on the face of undivided cube=4

Number of cubes with no face coloured= $(n-2)^{3}$

= $(4-2)^{3} =8$

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Also Check Out:

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Visual Reasoning – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
Cube and Cuboid – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
Dice – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts

Visual Reasoning – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts
Cube and Cuboid – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts
Dice – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts