Formulas for Set Theory

March 7, 2024

Set theory and its Formula

Set theory is a branch of mathematical logic that studies sets, which informally are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. Formulas for Set Theory are very useful in terms of exams.

Formulas for Set Theory

Formulas for Set Theory

Notations used in set theory:

  • n(A) – Cardinal number of set A.
  • n∘(A) – Cardinality of set A.
  • \overline{A} = Ac – complement of set A.
  • U – Universal
  • A ⊂ B – Set A is proper subset of subset of B.
  • A ⊆ B – Set A is subset of set B.
  • ∅ – Null set.
  • a ∈ A – element “a” belongs to set A.
  • A ∪ B – union of set A and set B.
  • A ∩ B – intersection of set A and set B.

Formulas

  1. If A and B are overlapping set, n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
  2. If A and B are disjoint set, n(A ∪ B) = n(A) + n(B).
  3. n(A) = n(A ∪ B) + n(A ∩ B) – n(B).
  4. n(A ∩ B) = n(A) + n(B) – n(A ∪  B).
  5. n(B) = n(A ∪ B) + n(A ∩ B) – n(A).
  6. n(U) = n(A) + n(B) – n(A ∩ B) + n((A ∪ B)c).
  7. n((A ∪ B)c) = n(U) + n(A ∩ B) – n(A) – n(B).
  8. n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B).
  9. n(A – B) = n(A ∪  B) – n(B).
  10. n(A – B) = n(A) – n(A ∩ B).
  11. n(Ac) = n(U)- n(A)

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Some Examples based On Above Formulas:

Question 1: If A = { 1, 4, 5, 8} and B = { 6, 8, 10, 12}. Find A ∩ B.

Answer: A∩B= {8}

set theory formulas

Question 2: Check whether A={8,7,6,9} and B={9,6,7,8} are equal sets?

Answer: Yes they are equal sets since all the elements of A are present In B.

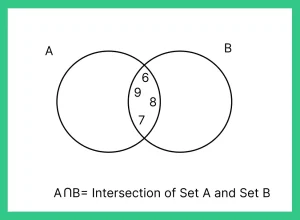
Set theory formula

Question 3: If A= { 7,8,0,6,8} B = { 5,6,7,8,9,0} Find A-B and B-A?

Answer: A-B= Elements in set a but not in b = { } null:

B-A= Elements in set b but not in a= {5, 9}.

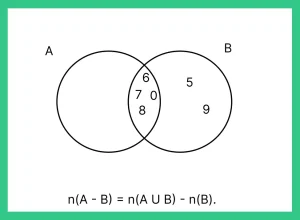
set theory formulas

Question 4:If A={1,2,3,4} B={3,5,6,9} and C={6,7,8,9} Find A∩(B ∪ C).

Answer: B ∪ C = {6,9}, A∩(B ∪ C) = { } null, as there is no element in common

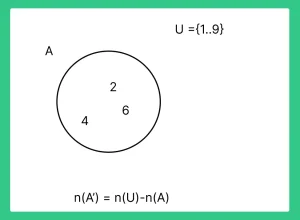
Set theory formulas

Question 5: If U={ 1,2,3,4,5,6,7,8,9} A= {2,4,6} Find A’.

Answer: A’ means all the elements except that in A.   {1,3,5,7,8,9}

Set theory formulas

Also Check Out

Set Theory question and answers
Tips Tricks and Shortcut for Set Theory
How to solve Set Theory Quickly?
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout