Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
PREPINSTA PRIME
How To Solve Quickly Permutation Combination
How to Solve Permutation and Combination Questions Quickly
How to solve Permutation and Combination Questions Quickly has been discussed on this page along with basic concepts.

Basic concept of Permutation and Combination
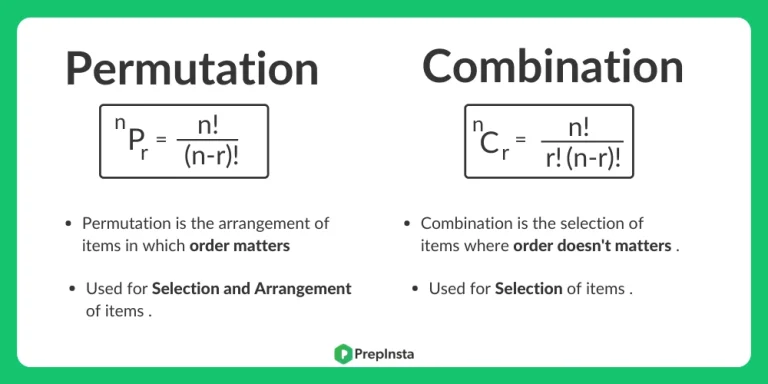
How to Solve Permutation and Combination Questions Quickly.
- Permutation is an arrangement of objects in a definite order.
- Number of all permutations of n things, taken r at a time, is given by
nPr = \mathbf{\frac{n!}{(n-r)!}} - Combination is selection of objects where order does not matter.
- Number of all combinations of n things, taken r at a time, is given by
nCr = \frac{n!}{(n-r)! r! } - Here we can easily understand how to solve permutation and combination easy.
Type 1: How to Solve Quickly Permutation and Combination Different ways to arrange (with repetition)
Question 1.How many 3 letter words with or without meaning can be formed out of the letters of the word MONDAY when repetition of words is allowed?
Options:
A. 125
B. 216
C. 120
D. 320
Solution: 6 * 6 * 6 = 216
OR
We can solve directly by formula nr = 63 = 216
Correct option: B
Question 2. In how many ways the letters in the word TOOTH can be arranged?
Options:
A. 120
B. 40
C. 20
D. 30
Solution: \frac{5!}{2! × 2! }
= \frac{5 × 4 × 3 × 2 × 1 }{2 × 1× 2 × 1 }
= \frac{120}{ 4}
= 30
Correct option: D
Question 3.How many three digit numbers can be formed using digits 2, 3, 4, 7, 9 so that the digits can be repeated.
Options:
A. 125
B. 360
C. 24
D. 6
Solution: Each place can be filled by any one of 5 digits
Total numbers = 5 * 5 *5 =125
OR
We can solve directly by formula nr = 53 = 125
Correct option: A
Type 2: Different ways to arrange (without repetition)
Question 1. How many five letter words with or without meaning, can be formed from the word ‘COMPLEXIFY’, if repetition of letters is not allowed?
Options:
A. 43200
B. 30240
C. 12032
D. 36000
Solution: 10P5 = \frac{10!}{(10 – 5)!} = 10 * 9 * 8 * 7 * 6 = 30240
Correct option: B
Question 2.In how many different ways can the letters of the word ‘LOGARITHMS’ be arranged so that the vowels always come together?
Options:
A. 6720
B. 241920
C. 40320
D. 360344
Solution: In such questions we treat vowels as one letter.
So the word becomes LGRTHMS (OAI)
It means there are total 8 letters. Therefore, number of ways of arranging these letters = 8! = 40320
Now, there are three vowels (OAI), number of ways of these letters can be arranged = 3! = 6
Required number of words = 40320 * 6 = 241920
Correct option: B
Question 3.How many three digit numbers can be formed from the digits 3, 4, 5, 7, 8, and 9. Also, the number formed should be divisible by 5 and no repetition is allowed?
Options:
A. 20
B. 24
C. 25
D. 10
Solution: The number which is divisible by 5 has 5 or 0 at one’s place. In this case we must have 5 at the unit place as 0 is not in the list.
There are total 6 digit out of which last digit is fixed by 5. Therefore, we are left with 5 digits (3, 4, 7, 8, 9) at the tens place.
Similarly, the hundred place can be filled by 4 digits.
So, required number = 4 * 5 * 1 = 20
Correct option: A
Type 3: How To Solve Permutation and Combination Question- (with repetition)
Question 1.An ice cream seller sells 5 different ice-creams. John wants to buy 15 ice creams for his friends. In how many ways can he buy the ice-cream?
Options:
A. 1450
B. 3768
C. 3876
D. 1540
Solution: r + n -1Cr = 15 + 5 – 1C15 =19C15
We know that, nCr = \frac{n!}{(n-r)! r! }
19C15 = \frac{19!}{(19-15)! 15! } = 3876
Correct option: C
Question 2.There are 5 types of soda flavor available in a shop. In how many ways can 10 soda flavors be selected?
Options:
A. 1454
B. 1001
C. 1211
D. 1540
Solution: r + n – 1Cr = 10 + 5 – 1C10 = 14C10
We know that, \frac{n!}{(n-r)! r! }
14C10 = \frac{14!}{(14-10)! 10! } = 1001
Correct option: B
Question 3. In how many ways can 16 identical toys be divide in 4 children?
Options:
A. 966
B. 696
C. 969
D. 996
Solution: r + n – 1Cr = 16 + 4 – 1C16 = 19C16
We know that, nCr = \frac{n!}{(n-r)! r! }
19C16 = \frac{19!}{(19-16)! 16! } = 969
Correct option: C
Type 4: Permutation and Combination Solve Question Quickly. (without repetition)
Question 1. A wooden box contains 2 grey balls, 3 pink balls and 4 green balls. Fins out in how many ways 3 balls can be drawn from the wooden box. Make sure that at least one pink ball is included in the draw?
Options:
A. 64
B. 46
C. 56
D. 65
Solution: According to the question, we have, (one pink and two non-pink balls) or (two pink and one non-pink balls) or (3 pink)
Therefore, required number of ways are (3C1 * 6C2) + (3C2 * 6C1) + (3C3) = 45 +18 + 1 = 64
Correct option: A
Question 2.There are 5 boys and 10 girls in a classroom. In how many ways teacher can select 2 boys and 3 girls to make a dance group?
Options:
A. 720
B. 1200
C. 240
D. 840
Solution: Required numbers of ways = 5C2 * 10C3 = 10 * 120 = 1200
Correct option: B
Question 3.There are 10 consonants and 5 vowels. Out of which how many words of 5 consonants and 2 vowels can be made?
Options:
A. 1270080
B. 120052
C. 210789
D. 720432
Solution: Number of ways of selecting (5 consonants out of 10) and (2 vowels out of 4) = 10C5 * 5C2 = 252
Number of ways of arranging 7 letters among themselves = 7!
=7 x 6 x 5 x 4 x3 x2 x 1
=5040
Required number of ways = (252 x 5040) = 12,70,080
Correct option: A
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Probability – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
Others
- Combination – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Circular Permutation – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Probability –
Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts
Others
- Combination –
Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Circular Permutation –
Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates




very clear… so much helpful
very helpful
This is a very well framed site to help everything better , really like it
type 2 questions were new to me.. thanks alot
Very interesting questions & helps to understand d concept
Thanking You and keep supporting us by which we will give you the best
these questions are really helps to understands the each and every concepts thank you prep ins teams keep it up
welcome Prakash Kumar
sir provide more question for practice
To practice more questions, kindly go through the given links:
https://prepinsta.com/paid-materials/
https://prepinsta.com/online-classes/