Quants Menu
- HCF and LCM
- Number System
- Number Decimals & Fractions
- Surds and Indices
- Divisibility
- Ages
- LCM
- HCF
- Inverse
- Speed Time and Distance
- Work and Time
- Boats and Streams
- Pipes and Cisterns
- Averages
- Allegations and Mixtures
- Ratio and Proportions
- Simple & Compound Interest
- Simple Interest
- Compound Interest
- Percentages
- Profit & Loss
- Successive Discount 1
- Successive Discount 2
- AP GP HP
- Arithmetic Progressions
- Geometric Progressions
- Harmonic Progressions
- Probability
- Permutation & Combination
- Combination
- Circular Permutation
- Geometry
- Heights and Distances
- Perimeter Area and Volume
- Coordinate Geometry
- Venn Diagrams
- Set Theory
- Algebra
- Linear Equations
- Quadratic Equations
- Logarithms
- Clocks
- Calendars
- Clocks and Calendars
- Finding remainder of large powers
PREPINSTA PRIME
How To Solve Geometry Questions Quickly
How To Solve Practical Geometry Problems
From the information provided on this page we will be learning about How to solve Geometry Questions Quickly of various types and how to apply problem solving techniques. Having knowledge about this will help you in solving more numbers of problems in less time.

Steps to Analyze and Solve Problems Quickly.
- Determine what the problem is asking about and then try to solve the problem.
- In geometry problems it is very much necessary to draw sketch of the problem solution as it helps you to reach to your solution quickly.
- Pay attention to units make sure that the units used are converted accordingly and all Numbers have same units.
- Solve the math you may use pythagoras theorem or other theorem’s to solve it
- Analyze your results and make sure they are correct.
Type 1: How to Solve Geometry Questions Quickly related to Lines and Angles
Ques. 1
In the figure above, AB = BC = CD = DE = EF = FG = GA. Then ∠DAE is approximately
Options
(a) 15°
(b) 20°
(c) 25°
(d) 30°
Explanation
Let us assume, DAE = x
Triangle ABC is isosceles as AB = BC –> BCA = CAB = x
Hence, CBD = CAB + BCA = x + x = 2x ………….. [External angle of triangle ABC]
Triangle BCD is isosceles as BC = CD –> CBD = CDB = 2x
Hence, DCE = DAE + CDA = x + 2x = 3x ………….. [External angle of triangle ACD]
Triangle CDE is isosceles as CD = DE –> DCE = DEC = AED = 3x
Similarly, ADE = EFD = AEF + DAE = EGF + DAE = (DAE + GFA) + DAE = DAE + DAE + DAE = 3x
Hence, in triangle ADE, ADE + DAE + AED = 3x + x + 3x = 7x
Hence, 7x = 180 —> x = 180/7 = 25.7.. ≈ 25
Correct Option (C)
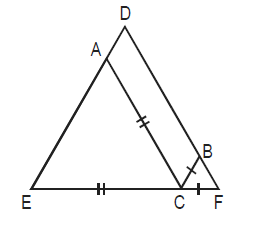
Ques. 2
In triangle DEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If ∠D=400, then ∠ACB =
Options:
(a) 140
(b) 70
(c) 100
(d) None of these
Explanation
Let the angle E be x in triangle (AEC),
then angle AEB= 180-2*x. Then in triangle DEF, angle F=180-(40+x).
Now in triangle BCF, angle BCF=2*x-100.
Now, angle ACB= 180-(180-2*x+2*x-100)=100
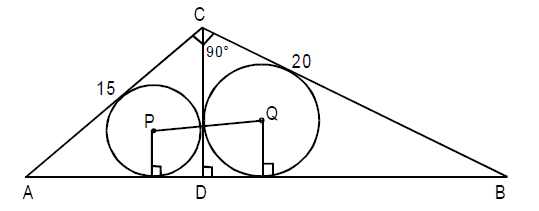
Ques. 3
In the above figure, ACB is a right-angled triangle. CD is the altitude. Circles are inscribed within the ΔACD and ΔBCD. P and Q are the centres of the circles. The distance PQ is
Options
(a) 5
(b) √50
(c) 7
(d) 8
Explanation
semi perimeter =\frac{15+9+12}{2} = 18.
On using the above equations we get inradius, r = 3.
Type 2: How to solve Geometry Questions of various shapes.
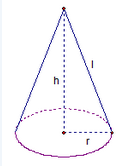
Ques. 4
Options
(a) 81π
(b) 90π
(c) 54π
(d) 9π
Explanation:
Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant heightLA = 2B
π(r)(l) = 2π(r2)
rl = 2r2
l = 2r
From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields
r2 + 92 = (2r)2
r2 + 81 = 4r2
81 = 3r2
27 = r2
B = π(r2) = 27π
LA = 2B = 2(27π) = 54π
SA = B + LA = 81π
Correct Options (A)
Ques. 5
You are given a right circular cone with height 5 cm. The radius is twice the length of the height. What is the volume?
Options
(a) 100πcm³
(b) 500πcm³
(c) 500/3 πcm³
(d) 50πcm³
Explanation:
You are given a right circular cone with height 5. The radius is twice the length of the height.
Height =5cm. The radius is twice of the height.
You are given a right circular cone with height 5. The radius is twice the height.
Radius = 2* Height
so the radius is 10 cm
Volume = πr² \frac{h}{3} \ = π(10)² \frac{5}{3} \ = \frac{500}{3} \ πr³
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Also Check Out
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Heights and Distances – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Perimeter Area and Volume – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Coordinate Geometry – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Venn Diagrams – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Set Theory – Questions | Formulas | How to Solve Quickly | Tricks & Shortcuts
- Heights and Distances – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Perimeter Area and Volume – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Coordinate Geometry – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Venn Diagrams – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts - Set Theory – Questions |
Formulas |
How to Solve Quickly |
Tricks & Shortcuts

 Apply For Jobs
Apply For Jobs Get Hiring Updates
Get Hiring Updates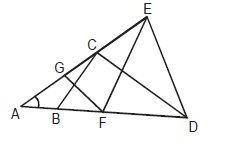





Login/Signup to comment