Compound Interest Formulas

July 15, 2023

Compound Interest Formulas in Aptitude

On this page we have discussed Compound Interest formulas, definition with examples.

Compound Interest in Maths
Compound interest is a concept in mathematics and finance that refers to the interest earned or paid on an initial amount of money, called the principal, as well as any accumulated interest from previous periods. Unlike simple interest, where interest is only calculated based on the initial principal, compound interest takes into account both the initial amount and the interest earned over time.

Formulas For Compound Interest CI

Compound Interest Formula

  • Compound interest is the interest calculated on the original principal and on the accumulated past interest of a deposit or loan. Compound interest is calculated based on the principal, interest rate (APR or annual percentage rate), and the time involved.

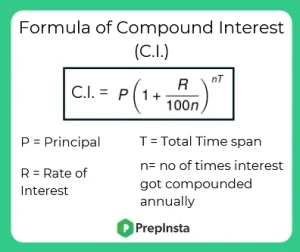
Formula of Compund Interest (CI) =  P (1+ \mathbf{\frac{r}{100n}})^{nT} – P

Formula of  Amount     =    CI +P

=   P (1+ \mathbf{\frac{r}{100n}})^{nT} – P + P

Here,  P = Principal

  r = rate of interest

  T = the number of years the amount is deposited or borrowed for.

  n= the number of times that interest is compounded per unit ‘t’.

Compound interest questions and answers
Times(in years)AmountInterest
1P\left ( 1-\frac{R}{100} \right )\frac{PR}{100}
2P\left ( 1-\frac{R}{100} \right )^2P\left ( 1-\frac{R}{100} \right )^2-P
3P\left ( 1-\frac{R}{100} \right )^3P\left ( 1-\frac{R}{100} \right )^3-P
4P\left ( 1-\frac{R}{100} \right )^4P\left ( 1-\frac{R}{100} \right )^4-P
nP\left ( 1-\frac{R}{100} \right )^nP\left ( 1-\frac{R}{100} \right )^n-P

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Important Compound Interest formulas

  • Formulas for Compound Interest (When Interest is Compound Annually)
    • Amount = P\mathbf{(1+ \frac{r}{100})^{T}}
    • Compound Interest =Total amount – Principal
    • Rate of interest (R) = [\mathbf{(\frac{A}{P})^{\frac{1}{T}}}− 1]%
  • Formulas of Compound Interest (When Interest is Compound Half Yearly)
    • Amount = P (1+ \mathbf{\frac{{\frac{r}{2}}}{100})^{2T}}
    • Compound Interest = Total amount – Principal
  • Compound Interest Formulas (When Interest is Compound Quarterly)
    • Amount = P (1+ \mathbf{\frac{{\frac{r}{4}}}{100})^{4T}}
    • Compound Interest = Total amount – Principal
  • Formulas of Compound Interest (When Interest is Compound Monthly)
    • Amount = P (1+ \mathbf{\frac{{\frac{r}{12}}}{100})^{12T}}
  • Compound Interest Formulas (When Interest is Compounded Annually but time is in fraction, say 2(\mathbf{\frac{3}{2}})years )
    • Amount = P (1+ \mathbf{\frac{r}{100}})^{2}(1+ \mathbf{\frac{\frac{3}{2}r}{100}})
  • Formulas of Compound Interest (When rates are different for different years)
    • Amount = P (1+\frac{r_{1}}{100}) (1+\frac{r_{2}}{100}) (1+\frac{r_{3}}{100})
  • Formulas for Compound Interest (Present worth of Rs. x due n years)
    • Present worth =    \frac{x}{(1+\frac{r}{100})}

Problems Based on Formulas Of  Compound interest with solutions

Question 1 . Find the amount on Rs 16000 for 3 year at 5% per annum compounded annually n.

[A] Rs. 18562

[B] Rs. 18550

[C] Rs. 18952

[D] Rs. 18552

Solution :     According to the formula of Compound Interest

Amount = P (1+ \mathbf{\frac{r}{100}})^{n}

Amount = 16000 (1+ \mathbf{\frac{5}{100}})^{3}

Amount = 16000 (1+ \mathbf{\frac{1}{20}})^{3}

Amount = 16000 (\mathbf{\frac{21}{20}})^{3}

Amount =18552

Correct Option: D

Question 2 . Find the  compound interest on Rs. 10,000 at 20% per annum for 5 years 4 months, compounded annually is :

[A] Rs. 16600

[B] Rs. 16544

[C] Rs. 15644

[D] Rs. 16500

Solution :    According to the Formula of Compound Interest ,

CI = P (1+ \mathbf{\frac{r}{100}})^{n} – P

CI = 10,000 (1+ \mathbf{\frac{20}{100}})^{5\frac{1}{3}} – 10,000
 
CI = 10,000 (1+ \mathbf{\frac{1}{5}})^{5\frac{1}{3}} – 10,000
 
CI = 10,000 (1+ \mathbf{\frac{1}{5}})^{5}(1+ \mathbf{\frac{1}{3*5}}) – 10,000
 
CI = 10,000 (1+ \mathbf{\frac{1}{5}})^{5}(1+ \mathbf{\frac{1}{3*5}}) – 10,000
 
CI = 10,000 (1+ \mathbf{\frac{1}{5}})^{5}(1+ \mathbf{\frac{1}{15}}) – 10,000
 
CI = 10,000 (\mathbf{\frac{6}{5}})^{5}(\mathbf{\frac{16}{15}}) – 10,000
 
On Solving ,
 
CI = 26544 – 10,000
 
CI = 16544
 
Correct Option: B
 
Question 3. Dobi borrowed a sum of Rs 78,000 at 10% p.a compound interest for 2 years. He repaid some amount at the end of 1st year. If Dobi cleared the debt by repaying Rs 35200 at the end of the 2nd year. How much did he repay at the end of 1st year?

                   [A] 72460

                   [B] 53800

                   [C] 18330

                   [D] 83787

Solution:   Using CI formula,
                   Total amount on compound interest
                  P = 78000
                  R= 10%
                  A = P(1+R/100)n
                  78000( 1 + \frac{10}{100}) = 85800
               Let us assume he repaid y Rs at the end of 1st year
               ( 85800 – y ) *( 1 + \frac{10}{100}) = 35200
               85800 – y = 32000

                y = 53800

Correct Option: 53800

 
Question 4 . If the compound interest on a sum of Rs 72000 at 10% p.a for t years is Rs 23832, what is the value of t?

               [A] 9

               [B] 1

               [C] 2

               [D] 3

Solution: As C.I for the 1st year = S.I

                        Interest for 1st year = 73000*\frac{10}{100}

                        = 7200 Rs

                        As interest on interest is C.I

                       Interest for the 2nd year = 7200 + 7200*\frac{10}{100}

                       = 7200 + 720 = 7920

                      Interest for the 3rd year = 7920 + 7920\frac{10}{100}

                      = 7920 + 792 = 8712

                     Total interest at the end of 3 years = 7200 + 7920 + 8712

                     = 23832

                    Therefore t = 3

Correct Option= 3

Question 5 . The Compound Interest on a certain amount at a certain rate of interest, for the 7th and 8th year, was Rs 2180 and Rs 2659.6 respectively. Find the rate of interest per annum.

                       [A] 3

                       [B] 12

                       [C] 22

                       [D] 28


Solution:     Using interest on interest is C.I
                       Let r be rate of interest
                       2180 + 21.8r = 2659.6
                       21.8r = 2659.6 – 2180
                       r = 22

 

Also Check Out

Compound Interest Question and Answer
How to solve Compound Interest Questions Quickly
Compound Interest Shortcuts, Tips and Tricks
Branding

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Others

Others