Construct Tree From Given Postorder And Preorder Traversal In C++

March 17, 2023

Construct Tree From Given Postorder And Preorder Traversal in C++

There are three types of traversals in a tree: Inorder, Preorder and Postorder Traversal. In this article, a tree is constructed using postorder and preorder traversal. In this article , we will learn about how to construct tree from given postorder and preorder traversal in C++.

Algorithm For PreOrder Traversal:

Print the node.
Traverse the left subtree.
Traverse the right subtree.

Algorithm For PostOrder Traversal:

Traverse the left subtree.
Traverse the right subtree.
Print the node.

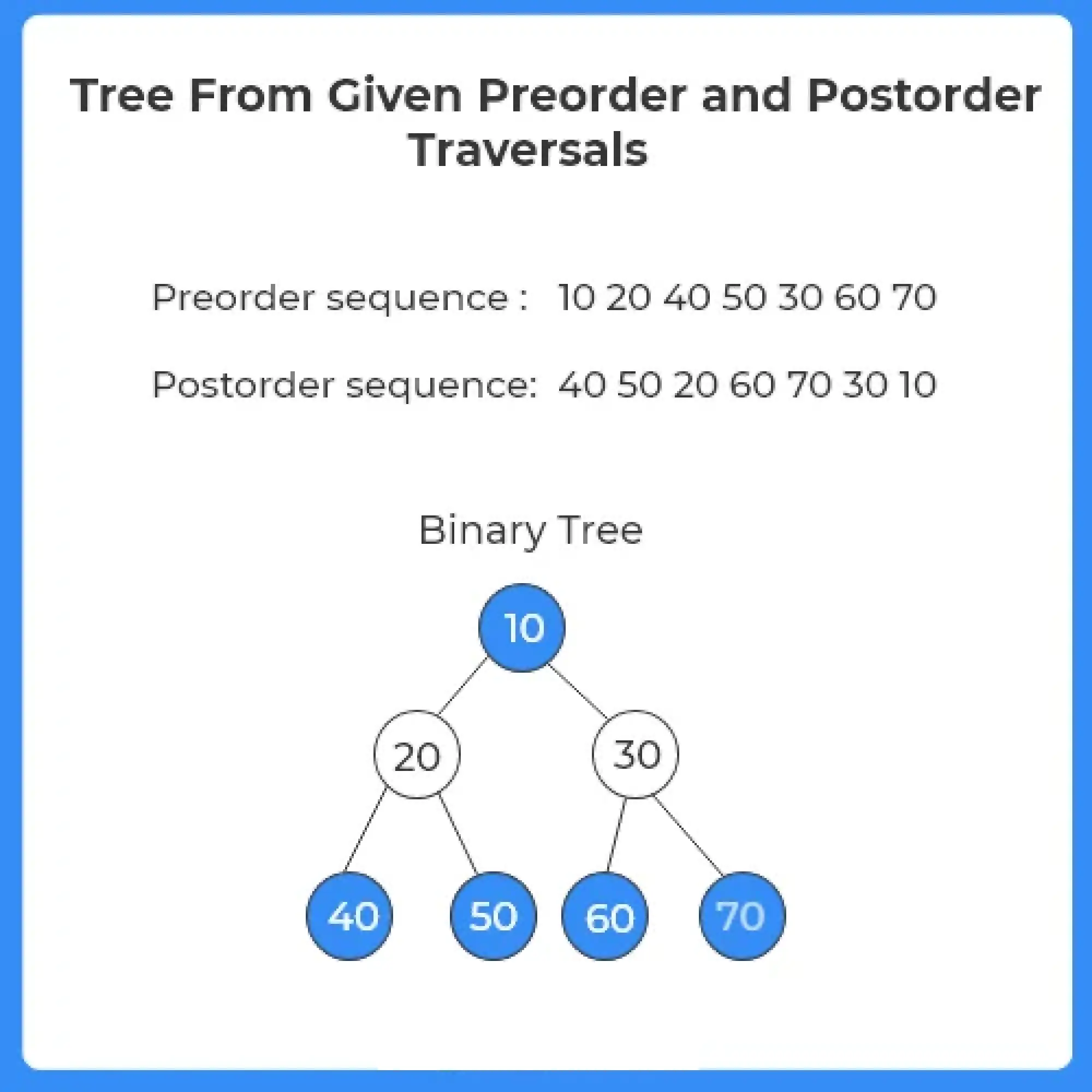
Algorithm:

Take the first element of preorder traversal and increase the count.
Find the index of the next element in the postorder traversal.
All the elements to the left including this element will be in the left subtree and other elements in the right subtree.
Recursively call for the right subtree too.
Repeat until array is traversed.

Depth First Traversals

Level Order Traversal

Construct Tree from given Inorder and Preorder traversals

Construct Tree from given Postorder and Inorder traversals

Find size of the Binary tree

Code Implementation for constructing tree from postorder and preorder traversals in C++

Run

#include<bits/stdc++.h> 
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};
int search (int postorder[], int start, int end, int element)
{
  int i;
  for (i = start; i <= end; i++)
    {
      if (postorder[i] == element)
	{
	  return i;
	}
    }
  return i;
}

void print_postorder (Tree * root)
{
  if (root == NULL)
    return;
  print_postorder (root->left);
  print_postorder (root->right);
  cout << root->data << " ";
}

Tree *build_tree (int preorder[], int postorder[], int presi, int preei, int postsi,int postei)
{
  if (presi > preei)
    {
      return NULL;
    }
  Tree *curr_node = new Tree (preorder[presi]);
  int x = curr_node->data;
  if (presi == preei)
    return curr_node;
  int search_index = search (postorder, postsi, postei, preorder[presi + 1]);
  int elements = search_index - postsi + 1;
  curr_node->left =
    build_tree (preorder, postorder, presi + 1, presi + elements, postsi,
		search_index);
  curr_node->right =
    build_tree (preorder, postorder, presi + elements + 1, preei,
		search_index + 1, postei - 1);

  return curr_node;
}

int main ()
{
  int preorder[] = { 10, 20, 40, 60, 70, 50, 30 };
  int postorder[] = { 60, 70, 40, 50, 20, 30, 10 };
  Tree *root = build_tree (preorder, postorder, 0, 6, 0, 6);
  cout << "Postorder traversal\n";
  print_postorder (root);
  return 0;
}

Output:

Postorder traversal
60 70 40 50 20 30 10

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java