Tree Traversals: Breadth-First Search (BFS)

February 3, 2026

Tree Traversals: Breadth First Search (BFS)

The term traversal means to visit each node in a tree exactly once. In linear lists the order of traversal is vividly first to last. However, in trees there exists no such natural linear order.

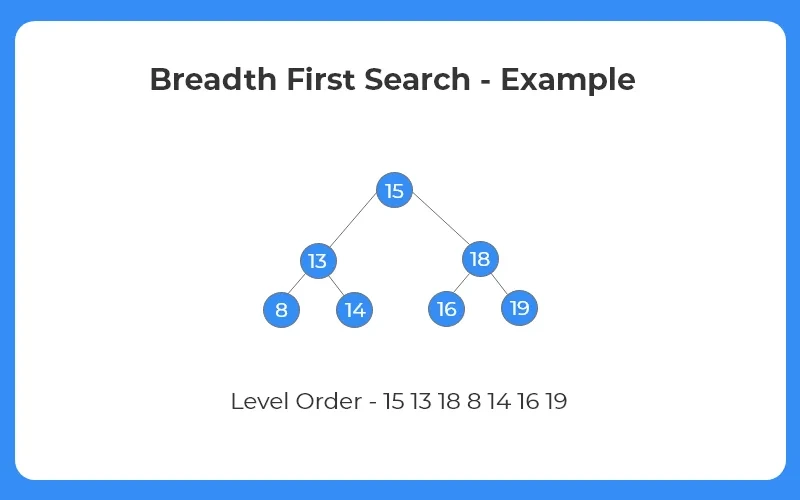
In Tree Traversal : Breadth-First Search (BFS) traversal visits tree nodes level by level, starting from the root and moving left to right at each level. It uses a queue data structure to ensure nodes are processed in the order they are discovered. This traversal is especially useful for finding the shortest path and analyzing the structure of a tree.

More Information About BFS:

BFS can be defined as an algorithm dedicated to traversing a tree structure, level by level or depth by depth.
This category of tree traversal initializes from the root node and explores all the adjacent nodes on a current level and then moves on to the next level, and so on.

Why Queue is better to traverse than Recursion?

Queues improves the time complexity because recursion gives the time complexity of O(2^n) in the worst case, whereas queue gives time complexity of O(n).
Height of the tree is first calculated to print level order but this is not required in queue.
Implementation is shorter in queues.

Algorithm (Queue):

If the root is NULL, return.
Otherwise push the root in queue.
Print the node’s data and add its left and right child.
Pop the node from the queue.
Repeat until the queue is empty.

Algorithm (Recursion):

Calculate height of tree.
Initialize loop from 0 to height
Recursive call for left and right subtree and decrease level by 1.
If level is 0, print the nodes

BST: Search in a Binary Search Tree

BST: Insertion in a Binary Search Tree

BST: Deletion in a Binary Search Tree

Traversals in Tree

Tree Traversals: Depth First Search (DFS)

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Code Implementation for Tree Traversal : Breadth-First Search (BFS) in C++

Run

#include<bits/stdc++.h>
using namespace std;

struct TreeNode
{
  int val;
  TreeNode *left;
  TreeNode *right;
    TreeNode (int x):val (x), left (NULL), right (NULL)
  { }
};

void bfs (TreeNode * root)
{
  queue <TreeNode*>q;
  q.push (root);

  while (!q.empty ())
    {
      int num_nodes = q.size ();

      for (int i = 0; i < num_nodes; i++)
	{
	  TreeNode *curr_node = q.front ();
	  q.pop ();

	  cout << curr_node->val << " "; if (curr_node->left)
	    {
	      q.push (curr_node->left);
	    }
	  if (curr_node->right)
	    {
	      q.push (curr_node->right);
	    }
	}
    }
}

int main ()
{
  TreeNode *root = new TreeNode (10);
  root->left = new TreeNode (20);
  root->right = new TreeNode (30);
  root->left->left = new TreeNode (40);
  root->left->right = new TreeNode (50);
  cout<<"BFS Traversal of the tree is : ";
  bfs (root);

  return 0;
}

Output:

10 20 30 40 50

Explanation:

The code defines a TreeNode structure where each node stores a value and pointers to its left and right child.
The bfs() function performs Breadth First Search using a queue to traverse the tree level by level.
The root node is pushed into the queue first, and nodes are processed until the queue becomes empty.
For every node removed from the queue, its value is printed and its left and right children are added to the queue if they exist.
In main(), a binary tree is manually created and the BFS traversal is called to display nodes in level order.

Time and Space Complexity:

Operation	Time Complexity	Space Complexity
BFS Traversal	O(n)	O(n)
Queue Operations	O(1) per operation	O(n)
Tree Node Creation	O(1) per node	O(1)
Total Program Execution	O(n)	O(n)

Conclusion:

Breadth First Search (BFS) is an important tree traversal technique that visits nodes level by level, starting from the root node. By using a queue, it ensures that all nodes at the current level are processed before moving to the next level, making the traversal systematic and easy to understand.

BFS is widely used in problems where level-wise processing is required, such as finding the shortest path or checking the structure of a tree. Its simple logic and predictable traversal order make it a reliable choice for many tree-based applications.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java