Searching In A Binary Search Tree In Java

March 17, 2023

Searching in a Binary Search Tree (BST)

A Binary Search Tree is a rooted binary tree whose internal nodes each a key greater than all the keys in the node’s left subtree and less than those in it’s right subtree. A Binary Search Tree is also called an ordered or sorted binary tree. In this article we will learn how to searching in a Binary search Tree.

search an element in binary search tree

Properties Of Binary Search Tree:-

  1. All the node’s in the left subtree are less than the root node.
  2. Similarly , All the node’s in right subtree are greater than the root node.
  3. The left and right subtree each must also be a binary search tree.

   These properties provides an ordering so that the operations like searching ,insertion, deletion, finding maximum key , minimum key can be done fast. 

Example for Searching in a Binary Search Tree

searching in a binary search tree

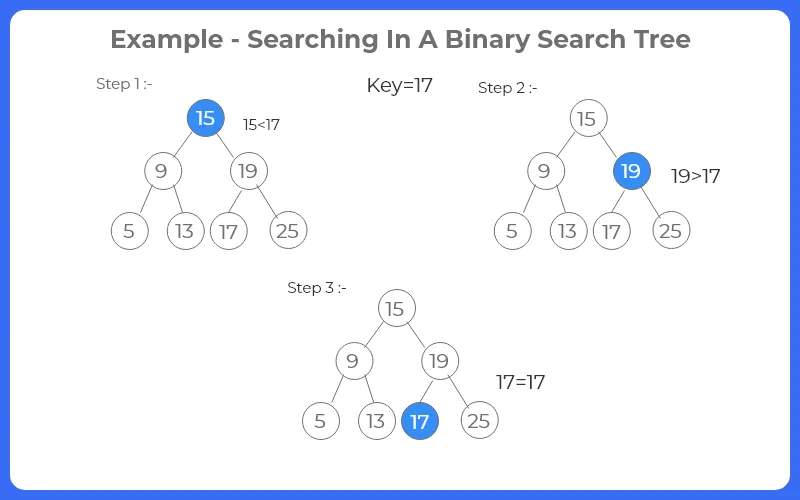
Steps to find a node in Binary Search Tree

Suppose we want to search 17 in the above example 

  • Step 1: Compare 17 with the root element which is 15. 
  • Step 2: 17>15 , so Search for a node in right subtree.
  • Step 3: Compare 17 with 19 . i.e. 17<19 , so search for an element in left subtree.
  • Step 4: compare 17 with the left child of 19 . i.e. 17==17 , Hence, stop searching and return true.
DSA desktop gif
DSA mobile gif

Preorder Tree Traversal without Recursion

BST: Search a node in Binary Search Tree

Binary search tree in Data Structures (Introduction)

Insertion in a Binary Search Tree

Algorithm:

BinarySearchTree(tree):

  1. Compare the node with the root of the tree.
  2. If the node is matched then return the node itself.
  3. Otherwise check if node value is less than the element present on root, If so then move to left subtree.
  4. If node value is greater than the element present on root then move to the right subtree.
  5. Repeat this procedure recursively until match found .
  6. If element is not found then return null.

Code For Binary Search Tree​

Run 
//Searching in Binary Tree


import java.util.*;
/*Representing a Node of a binary tree */
class Node{
    int value;
    Node left,right;
    Node(int value)
    {
        this.value=value; 
        left=null;
        right=null;
     }
}
class SearchNode
{
    Node root; //root of a binary search tree
    SearchNode()
    {
        root=null;
     }
    public Node searchNode(Node root,int value)
    {
        if(root==null)
            return null;
        if(root.value==value)   // return true if value is found in binary tree
            return root;
        else if(value <root.value)  
            return searchNode(root.left,value);  //traverse left subtree
        else 
            return searchNode(root.right,value);  //traverse right subtree
    }
    
}
public class Main{
    public static void main(String[] args) 
    {
        //Adding Nodes to the binary tree
        SearchNode tree=new SearchNode();
        tree.root=new Node(15);
        tree.root.left=new Node(9);
        tree.root.right=new Node(19);
        tree.root.left.left=new Node(5);
        tree.root.left.right=new Node(13);
        tree.root.right.left=new Node(17);
        tree.root.right.right=new Node(25);
        //calling search function if element is found then it will return true else return false
        Node node=tree.searchNode(tree.root,17);   
        if(node!=null)
            System.out.println("Element "+node.value+" is found in binary  tree");
         else 
            System.out.println("Element is not found in binary tree");
    }
}

Output :

Element 17 is found in binary  tree

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java