Insertion In Binary Search Tree In Java
Insertion In Binary Search Tree
Here you will learn about Insertion in Binary search tree in java programming language.
Binary Search Tree is a rooted binary tree whose internal nodes each a key greater than all the keys in the node’s left subtree and less than those in it’s right subtree. Insertion function is used to add new element in a binary search tree at appropriate position. In this article we will perfom insertion in binary search tree using recursion in java.
Insertion In Binary Search Tree In Java
Why Do We Need Insertion in BST?
Insertion helps in:
- Dynamically building the tree
- Maintaining sorted order
- Supporting efficient search operations
- Implementing real world systems like:
Databases indexing
Autocomplete systems
File systems
Basic Idea of BST Insertion
Algorithm(ROOT, ITEM):
- If ROOT is null , Allocate the memory for ROOT.Set the ITEM to value and left and right pointer of ROOT , point to null.
- Check if the ITEM is less than the root element of the tree , if it is true then recursively perform this operation to the left of the tree.
- Else if the ITEM is greater than the root , then recursively perform this operation for the right of the tree.
- Insert a node where null is encountered.
- Return the ROOT of the tree.
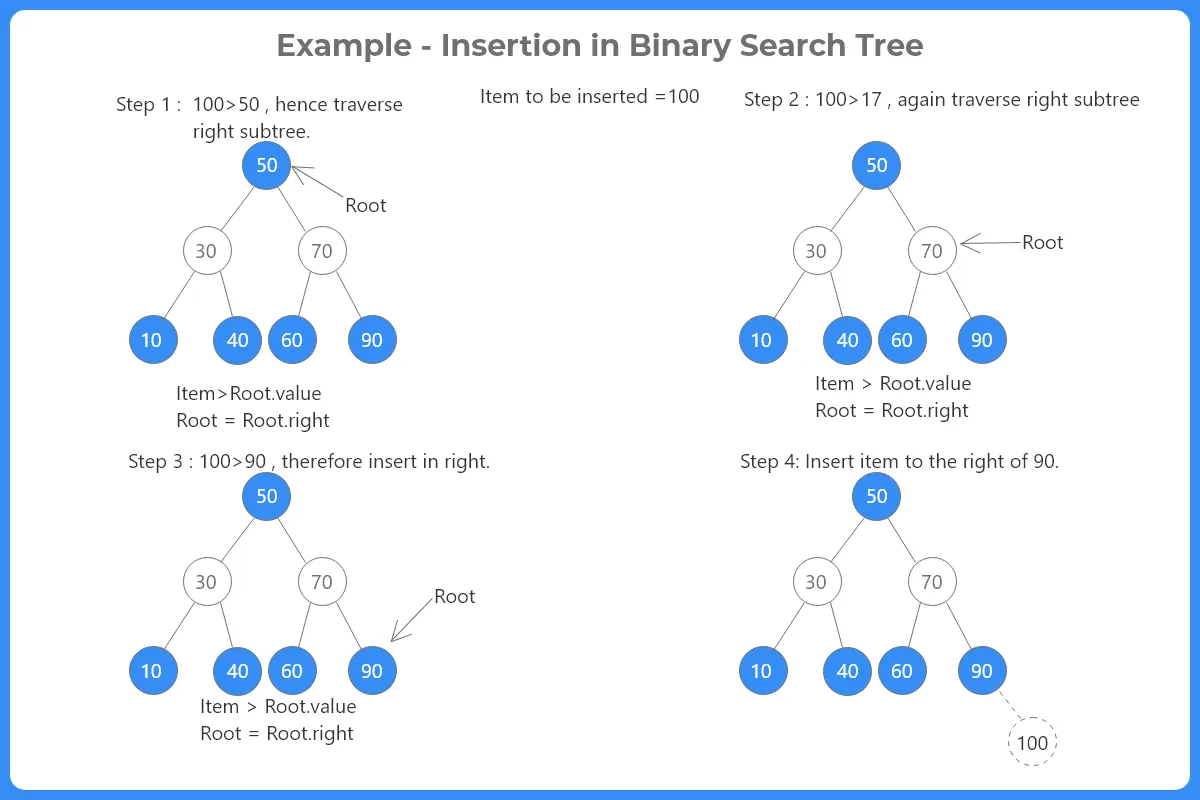
Example of Insertion In Binary Search Tree
Java Code for Insertion In Binary Search Tree
class Node {
int data;
Node left, right;
Node(int value) {
data = value;
left = right = null;
}
}
public class BSTInsertion {
// Function to insert a node in BST
public static Node insert(Node root, int key) {
// Base case: if tree is empty
if (root == null) {
return new Node(key);
}
// If key is smaller, go to left subtree
if (key < root.data) {
root.left = insert(root.left, key);
}
// If key is greater, go to right subtree
else if (key > root.data) {
root.right = insert(root.right, key);
}
// Return unchanged root
return root;
}
// Inorder traversal (to verify BST)
public static void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
public static void main(String[] args) {
Node root = null;
// Insert values
root = insert(root, 10);
insert(root, 5);
insert(root, 15);
insert(root, 2);
insert(root, 7);
// Print BST (Inorder traversal)
System.out.print("Inorder Traversal: ");
inorder(root);
}
}
Input
Insert: 10, 5, 15, 2, 7
Output
Inorder Traversal: 2 5 7 10 15
Worst Case (Skewed Tree): O(n)
h = height of tree
Worst case: O(n), Best case: O(log n)
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Frequently Asked Questions
Answer:
It is the process of adding a new node into a BST while maintaining its ordering property.
Answer:
It compares the value with nodes and places it in the correct position recursively or iteratively.
Answer:
Typically, duplicates are ignored or handled based on custom rules (like storing count or placing consistently on one side).
Answer:
It is O(log n) for balanced trees and O(n) for skewed trees.
Answer:
It helps maintain a sorted structure that allows efficient searching, deletion, and traversal.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Singly Linked List
- Introduction to Linked List in Data Structure
Click Here - Linked List in –
- Singly Linked List in –
- Insertion in singly Linked List –
- Insertion at beginning in singly Linked List –
- Insertion at nth position in singly Linked List –
- Insertion at end in singly Linked List –
- Deletion in singly Linked List –
- Deletion from beginning in singly linked list :
- Deletion from nth position in singly linked list :
- Deletion from end in singly linked list :
- Linked List Insertion and Deletion –
C | C++ | Java - Reverse a linked list without changing links between nodes (Data reverse only) –
C | C++ | Java - Reverse a linked list by changing links between nodes –
- Print reverse of a linked list without actually reversing –
- Print reverse of a linked list without actually reversing –
- Insertion in the middle Singly Linked List –
- Insertion in a Sorted Linked List –
- Delete alternate nodes of a Linked List –
- Find middle of the linked list –
- Reverse a linked list in groups of given size –
- Find kth node from end of the linked list –
- Append the last n nodes of a linked list to the beginning of the list –
- Check whether linked list is palindrome or not –
- Fold a Linked List –
- Insert at given Position –
- Deletion at given Position –
Singly Linked List
- Introduction to Linked List in Data Structure
- Linked List in – C | C++ | Java
- Singly Linked List in – C | C++ | Java
- Insertion in singly Linked List – C | C++ | Java
- Deletion in singly Linked List – C | C++ | Java
- Reverse a linked list without changing links between nodes (Data reverse only) – C | C++ | Java
- Linked List Insertion and Deletion – C | C++ | Java
- Reverse a linked list by changing links between nodes – C | C++ | Java
- Linked List insertion in the middle – C | C++ | Java
- Print reverse of a linked list without actually reversing – C |C++ | Java
- Search an element in a linked list – C | C++ | Java
- Insertion in a Sorted Linked List – C | C++ | Java
- Delete alternate nodes of a Linked List – C | C++ | Java
- Find middle of the linked list – C | C++ | Java
- Reverse a linked list in groups of given size – C | C++ | Java
- Find kth node from end of the linked list – C | C++ | Java
- Append the last n nodes of a linked list to the beginning of the list – C | C++ | Java
- Check whether linked list is palindrome or not – C | C++ | Java
- Fold a Linked List – C | C++ | Java
- Insert at a given position – C | C++ | Java
- Delete at a given position – C | C++ | Java
Login/Signup to comment