Tree Traversal : Depth First Search (DFS)

August 25, 2021

Tree Traversal : Depth First Search (DFS)

Depth-first search (DFS) is an algorithm for traversing or searching tree data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

Depth First Search Tree Traversal

Example - Depth First Search (DFS)

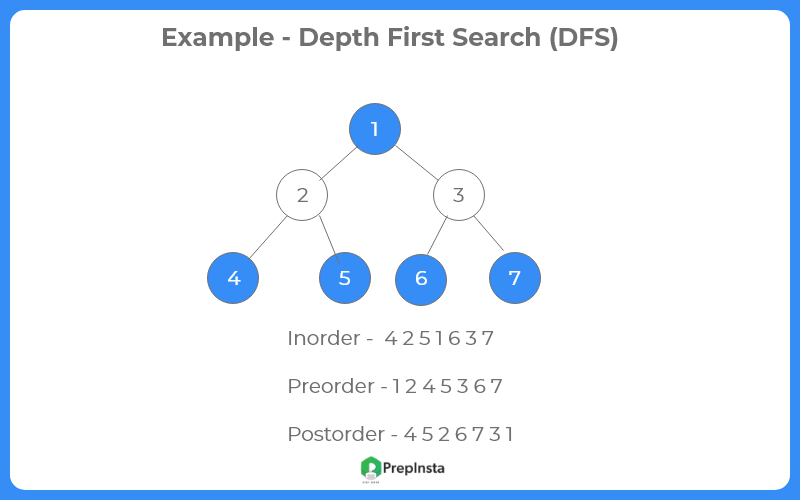
Example of Depth First Searach Tree Traversal

Given below are the three Tree Traversal through Depth First Search using recursion :-

1) Inorder Traversal : In inorder traversal, the left subtree is visited first, then the root and later the right sub-tree. Inorder traversal for the above example is 4 2 5 1 6 3 7.

Algorithm inorder(tree)

  1.   Recursively traverse left subtree.
  2.   Visit root node.
  3.   Recursively traverse right subtree.

2) Preorder Traversal : In preorder traversal , the root node is visited first, then the left subtree and finally the right subtree. Preorder Traversal for the above example is 1 2 4 5 3 6 7.

   Algorithm  preorder(Tree):

  1. Visit root node.
  2. Recursively traverse left subtree.
  3. Recursively traverse right subtree.

3)Postorder Traversal : In postorder traversal , first we traverse the left subtree, then the right subtree and finally the root node. Postorder traversal for the above example is 4 5 2 6 7 3 1.

Algorihtm postorder(Tree):

  1. Recursively traverse left sub-tree.
  2. Recursively traverse right sub-tree.
  3. Visit root node.

CODE FOR DEPTH FIRST SEARCH IN JAVA 

import java.util.*;
/*Representing node of a tree */
class Node 
{
    int value;
    Node left,right;
    Node(int value)
    {
        this.value=value;
        left=right=null;
     }
}
class DepthFirstSearch
{
    Node root; //Root of a Binary Tree
    DepthFirstSearch()
    {
        root=null;
    }
    /*inorder traversal of binary tree */
    public void inorder(Node ptr)
    {
        if(ptr==null)
        return ;
        /*first traverse left child */
        inorder(ptr.left);
        /*then print the value of node */
        System.out.print(ptr.value+" ");
        /* now traverse the right child */
        inorder(ptr.right);
    }
    /*preorder traversal of binary tree */  
    public  void preorder(Node ptr)
    {
        if(ptr==null)
        return ;
        /*first print the value of node*/  
        System.out.print(ptr.value+" ");
        /*then traverse the left child */
        preorder(ptr.left);
        /*now traverse the right child*/
        preorder(ptr.right);
    }
    /*postorder traversal of binary tree */
    public  void postorder(Node ptr)
    {    
        if(ptr==null)
            return ;
        /*first traverse left child*/   
        postorder(ptr.left);
        /*then traverse the right child*/
        postorder(ptr.right);
        /*now print the value of node*/
        System.out.print(ptr.value+" ");
    }
    public static void main(String[]  args)
    {
        DepthFirstSearch dfs=new DepthFirstSearch();
        //Creating nodes of a tree
        dfs.root=new Node(1);
        dfs.root.left=new Node(2);
        dfs.root.right=new Node(3);
        dfs.root.left.left=new Node(4);
        dfs.root.left.right=new Node(5);
        dfs.root.right.left=new Node(6);
        dfs.root.right.right=new Node(7);
        System.out.println("Binary Tree Inorder Traversal");
        dfs.inorder(dfs.root);
        System.out.println();
        System.out.println("Binary Tree Preorder Traversal");
        dfs.preorder(dfs.root);
        System.out.println();
        System.out.println("BinaryTree Postorder Traversal");
        dfs.postorder(dfs.root);
    }
}

 

Output:

Binary Tree Inorder Traversal
4 2 5 1 6 3 7
Binary Tree Preorder Traversal
1 2 4 5 3 6 7
BinaryTree Postorder Traversal
4 5 2 6 7 3 1

Space And Time Complexity for DFS

Time Complexity:

O(n)

Space Complexity :

O(n)