B Tree: Deletion

March 7, 2023

Deletion In B-Tree:

On this page we will discuss about Deletion in B-Tree in C .  B – Tree can be defined as a multi-way search tree of order m. All the values of a node that appear on the leftmost child of the node are smaller than the first value of that node. Similarly, all the values that appear on the rightmost child of a node are greater than the last value of that node.

Deletion in B-Tree

Deletion In B-Tree In C

The deletion of nodes in a B-Tree can be broadly classified into two vivid cases:
  • deletion at leaf node.
  • deletion at internal node.
Let us say the node to be deleted is called the target key. The target key can either be at the leaf node or an internal node. Let us now consider the various cases that follow:

Example:

Let us consider the given tree. From the given tree we are to delete the following elements:

A = 20 , 53 , 89 , 90 , 85.

Assuming we have order = 5; minimum keys = ⌈ m/2⌉ – 1 = 2; maximum keys = ⌈ m/2⌉ + 1 = 4; minimum children = ⌈ m/2⌉ = 3
maximum children = m = 5

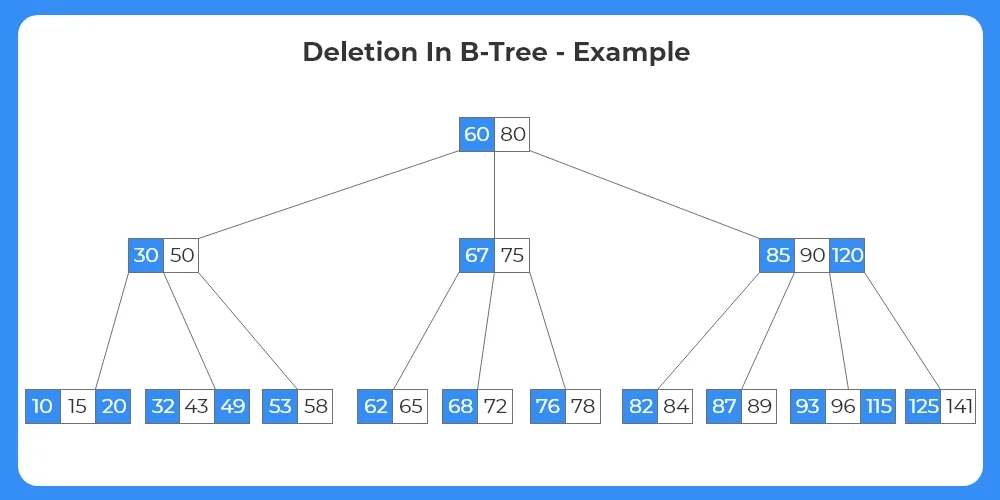
B Tree Deletion in C++

1. If the target key is at the leaf node:

If the target key is at the leaf node, we further study the given data to check if any of the following cases exist:

  • Case 1: If the leaf node consists of the min number of keys according to the given degree/order, then the key is simply deleted from the node.
  • Case 2: If the leaf contains the minimum number of keys, then:
  • Case 2a: The node can borrow a key from the immediate left sibling node,if it has more than the minimum number of keys.The transfer of the keys take place through the parent node, i.e, the maximum key of the left sibling moves upwards and replaces the parent; while the parent key moves down to the target node from where the target key is simply deleted.
  • Case 2b: The node can borrow a key from the immediate right sibling node, if it has more than the minimum number of keys.The transfer of the keys take place through the parent node, i.e, the minimum key of the right sibling moves upwards and replaces the parent; while the parent key moves down to the target node from where the target key is simply deleted.
  • Case 2c: If neither of the siblings have keys more than the minimum number of keys required then, merge the target node with either the left or the right sibling along with the parent key of respective node.

2.If the target key is at the internal node:

If the target key is at an internal node, we further study the given data to check if any of the following cases exist:

  • Case 1: If the left child has more than the minimum number of keys, the target key in the internal node is replaced by its inorder predecessor ,i.e, the largest element of the left child node.
  • Case 2: If the right child has more than the minimum number of keys, the target key in the internal node is replaced by it’s inorder successor ,i.e, the smallest element of the right child node.

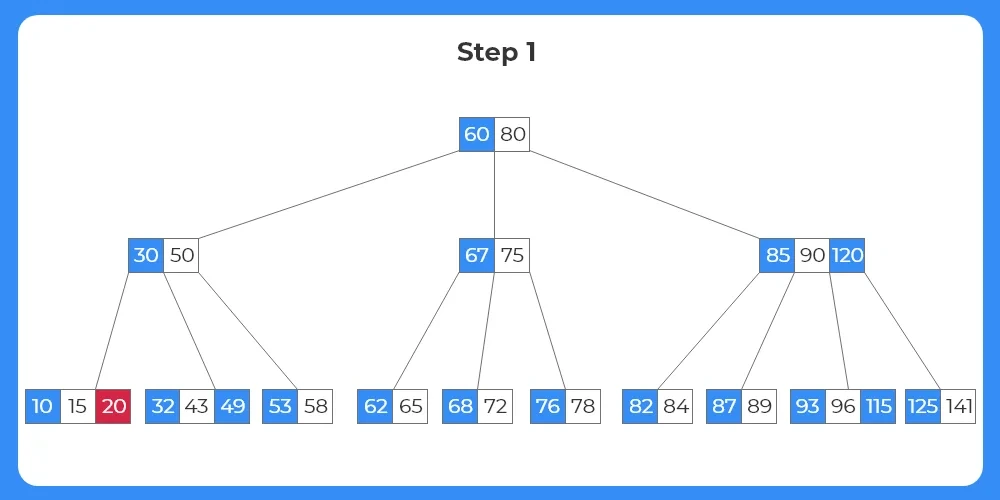
Step 1:

  • The first element to be deleted from the tree structure is 20.
  • We can see the key lies in the leaf node.
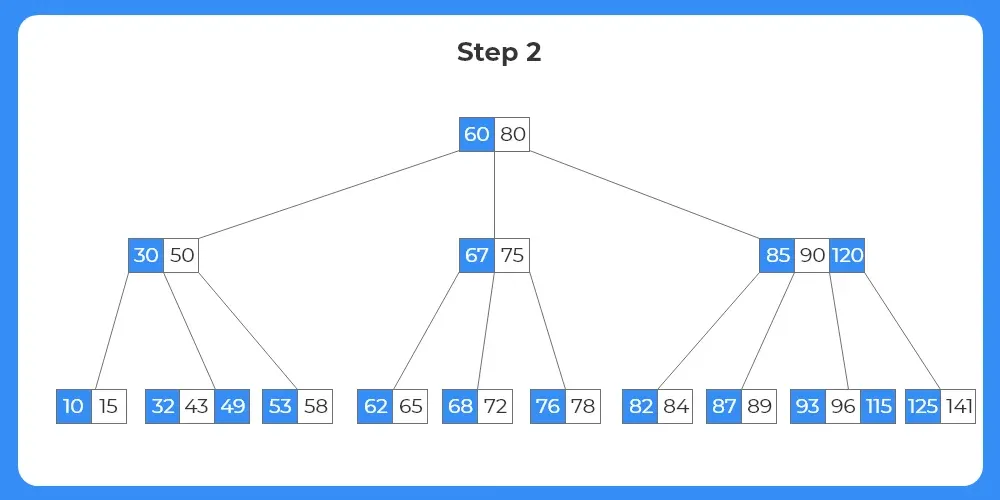
B tree Deletion in C++

Step 2:

  • The key 20 exists in a leaf node.
  • The node has more than the minimum number of keys required.
  • Thus the key is simply deleted from the node.
  • The tree after deletion is shown as follows.
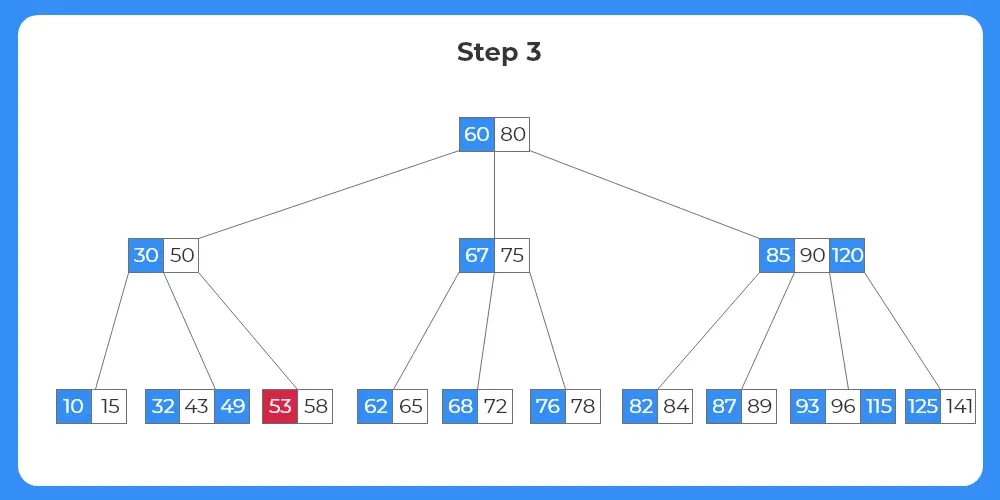
B Tree - Deletion in C++

Step 3:

  • The next element to be deleted from the tree is 53.
  • We can see from the image that the key exists in the leaf node.
B Tree - Deletion

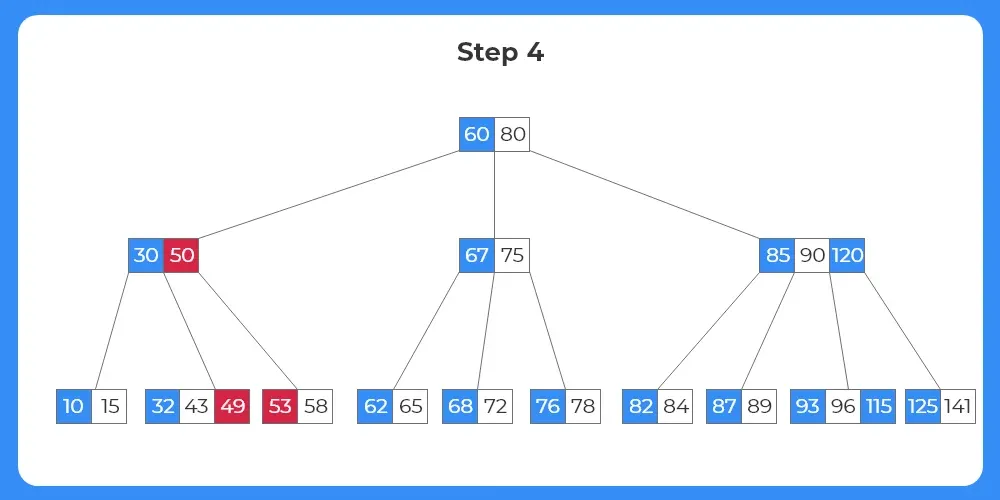
Step 4:

  • Since the node in which the target key 53 exists has just the minimum number of keys, we cannot delete it directly.
  • We check if the target node can borrow a key from it’s sibling nodes.
  • Since the target node doesn’t have any right sibling, it borrows from the left sibling node.
  • As we have studied above how the process of borrow and replace takes place, we apply it to the given structure.
B Tree - Deletion 4

Step 5:

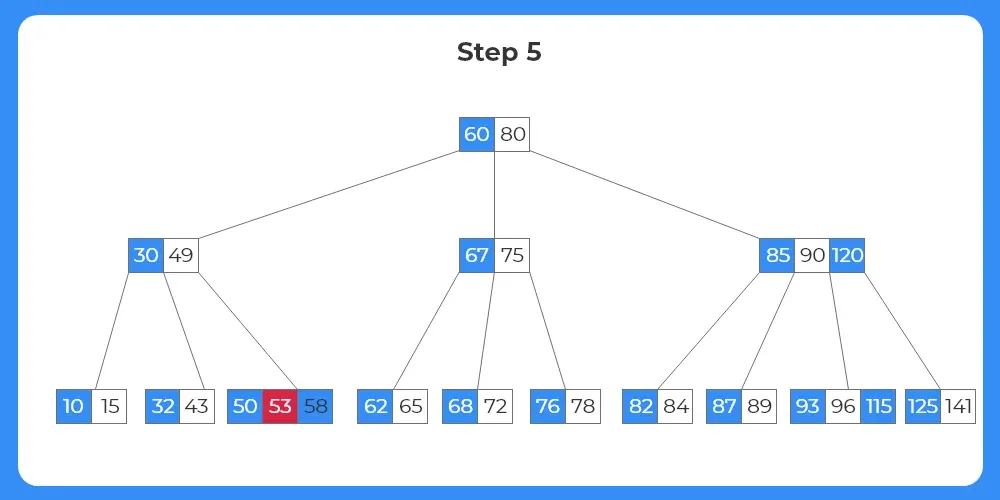
  • The key 49 moves upwards to the parent node.
  • The key 50 moves down to the target node.
B Tree - Deletion in java

Step 6:

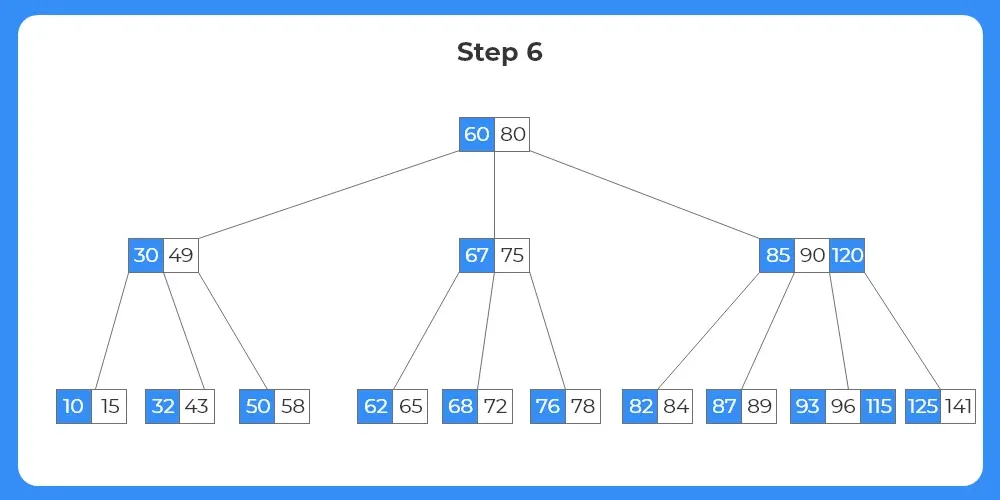
  • Now, since the target node has keys more than the minimum number of keys required, the key can be deleted directly.
  • The tree structure after deletion is shown as follows.
B Tree - Deletion

Step 7:

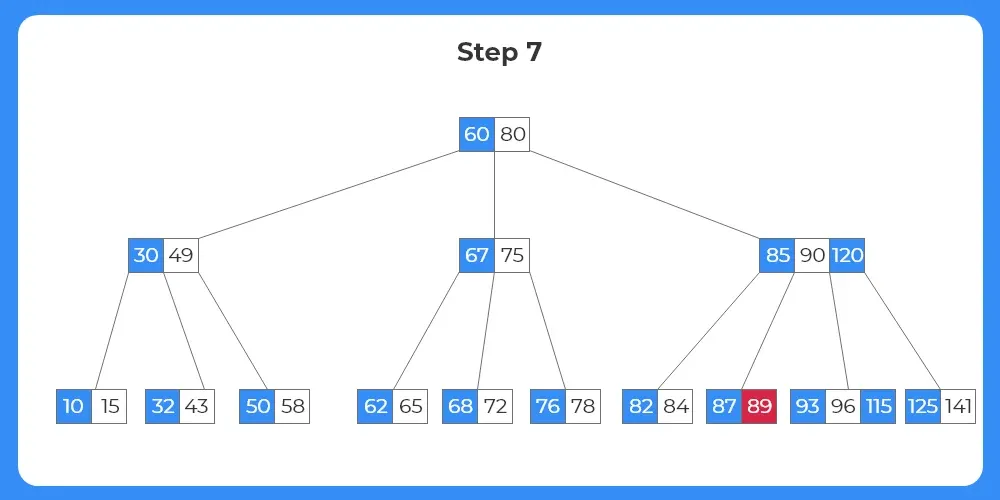
  • The next element to be deleted is 89.
  •  The target key lies within a leaf node as seen from the image.
B Tree - Deletion

Step 8: 

  • Again, the target node holds just the minimum number of keys required and hence the node cannot be deleted directly.
  • The target node now has to borrow a key from either of it’s siblings.
  • We check the left sibling; it also holds just the minimum number of keys required.
  • We check the right sibling node; it has one more than the minimum number of nodes  so the target node can borrow a key from it.
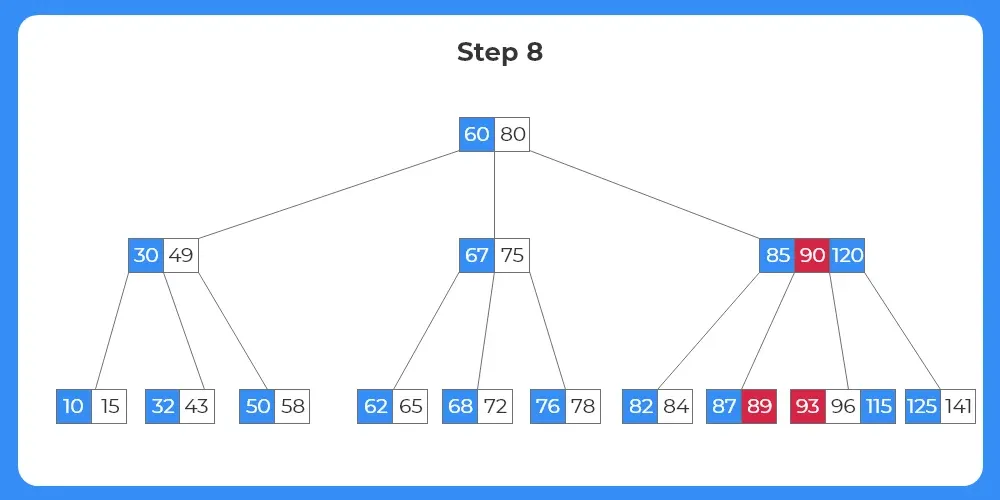
B Tree - Deletion
DSA desktop gif
DSA mobile gif

BST: Binary Search Tree Program

BST: Search a node in Binary Search Tree

BST: Insertion in a Binary Search Tree

Tree Traversals: Depth First Search (DFS)

B-Tree

B-Tree: Insertion

Step 9:

  • The key 93 moves up to the parent node.
  • The parent key 90 moves down to the target node.
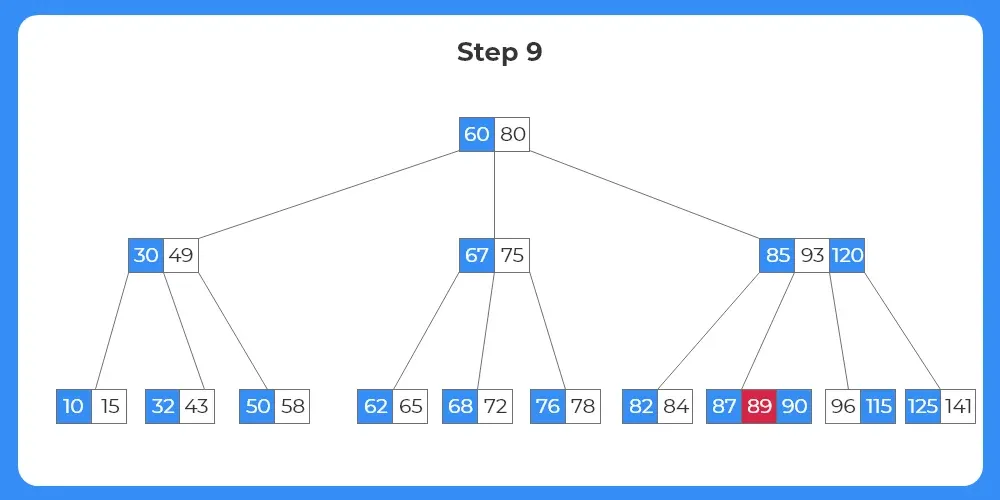
B Tree - Deletion

Step 10:

  • Now, as the target node has sufficient number of keys the target key can directly be deleted from the target node.
  • The tree structure after deletion is shown as follows. 
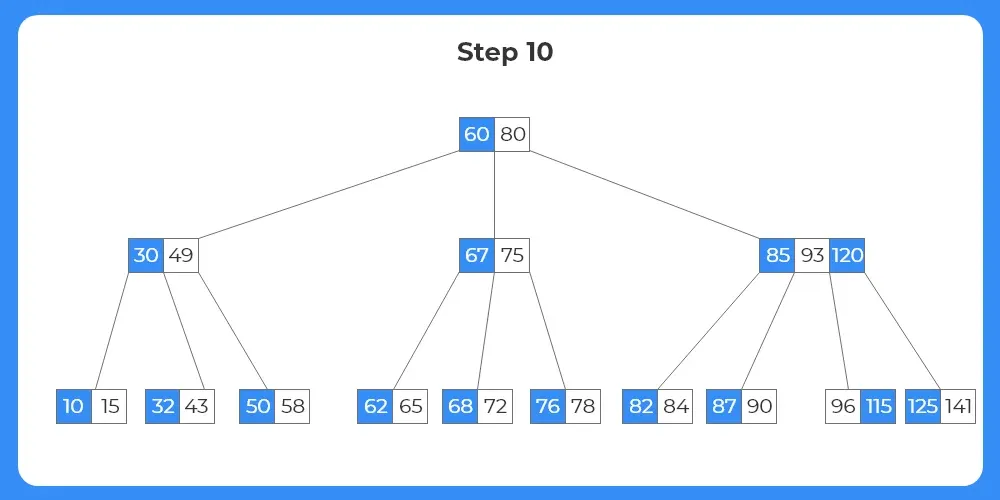
B Tree - Deletion

Step 11:

  • The next key to be deleted is 90.
  • The key exists within a leaf node as shown in the image.
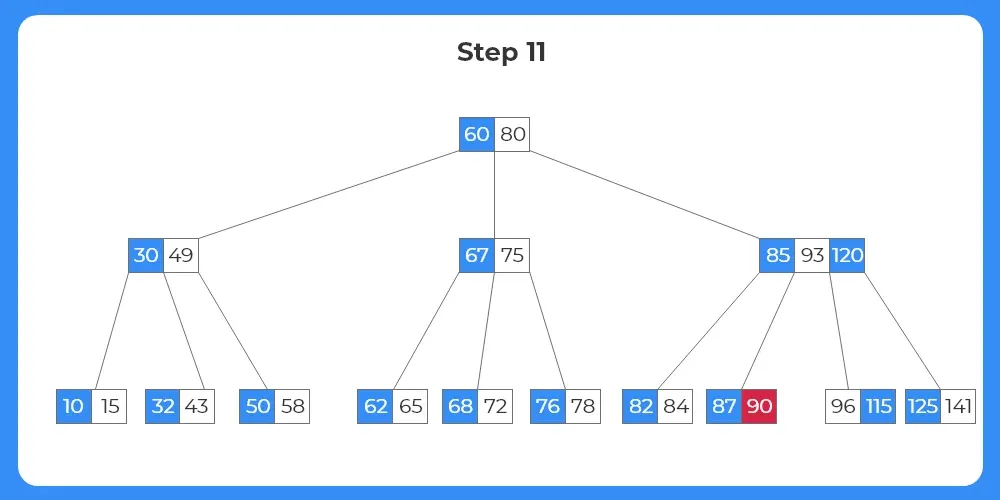
B Tree - Deletion

Step 12:

  • We can see that the target node has just the minimum number of keys.
  • The target node has to borrow a key from either of it’s siblings.
  • Since each of the siblings just have the number of the minimum keys, it cannot borrow the keys directly.
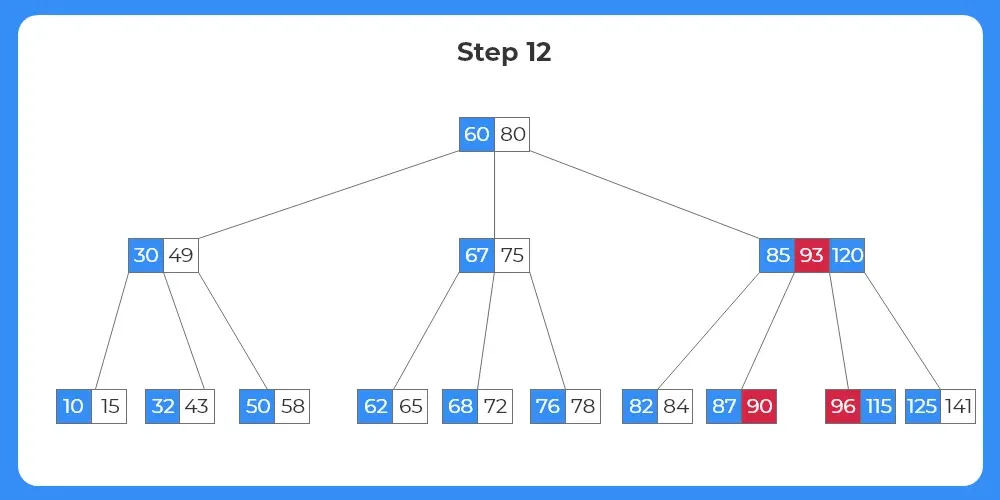
B Tree - Deletion

Step 13:

  • Since the target node cannot borrow from either of the siblings, we merge the target node, either of the sibling node and the corresponding parent to them.
  • The process of merging is shown as follows.
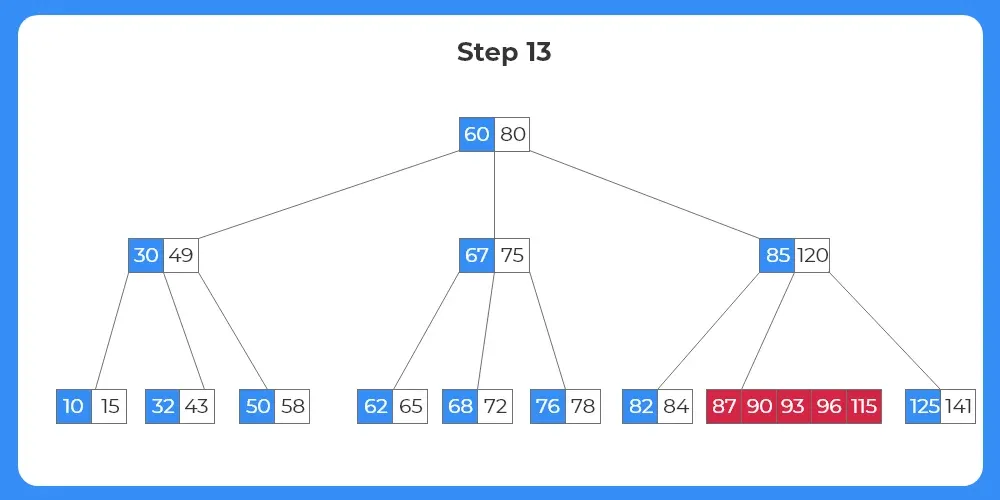
B Tree - Deletion

Step 14:

  • Since the target node now has sufficient number of keys, the target key 90 can be deleted directly.
  • The tree structure after the deletion of the element is shown as follows.
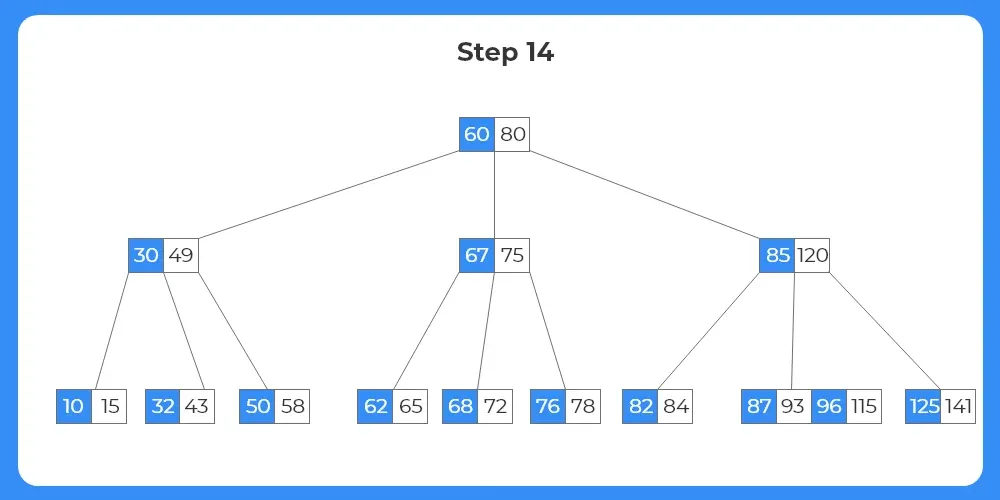
B Tree - Deletion

Step 15:

  • The next target node is 85.
  • Now here the node to be deleted is not a leaf node but an internal node.
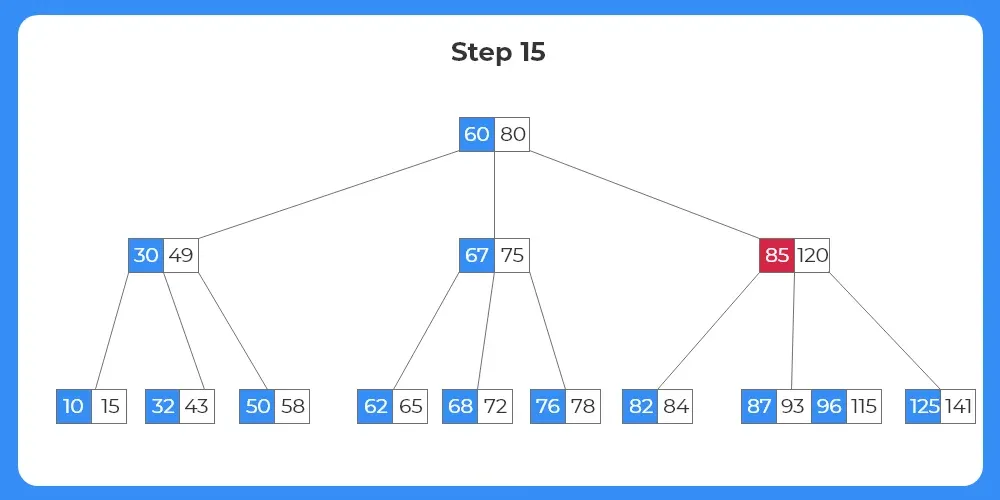
B Tree - Deletion

Step 16:

  • In case, when an internal node is to be deleted, we replace the key with it’s inorder predecessor or inorder successor.
  • We can select either of the child nodes if they have sufficient number of keys.
  • But as we can see in this case the target internal node can only borrow from it’s right child, i.e, inorder predecessor.
  • The key 85 moves down to the child node; key 87 moves up to the parent node.
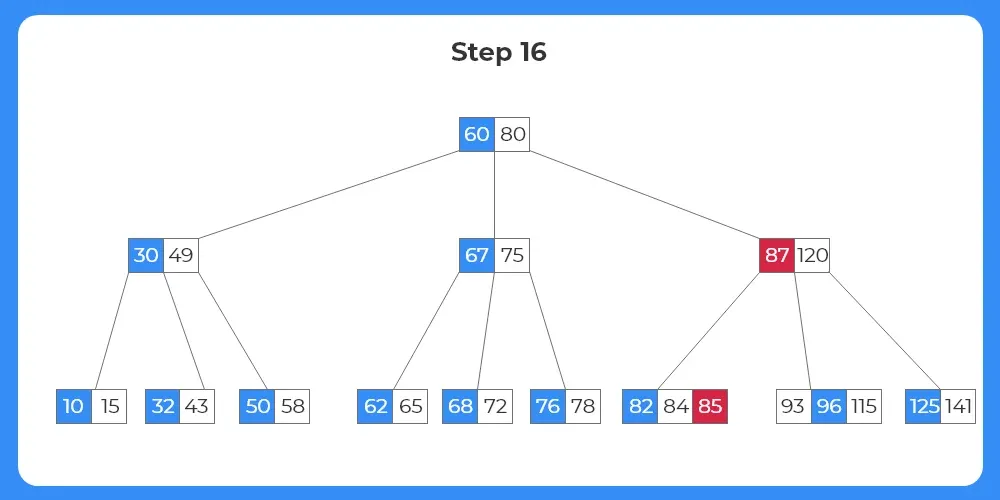
B Tree - Deletion

Step 17:

  • Now, as the target key is moved to the leaf node, it can be simply deleted from the leaf node.
  • The final tree structure after deletion of various nodes and preserving the b-tree properties is shown as follows.
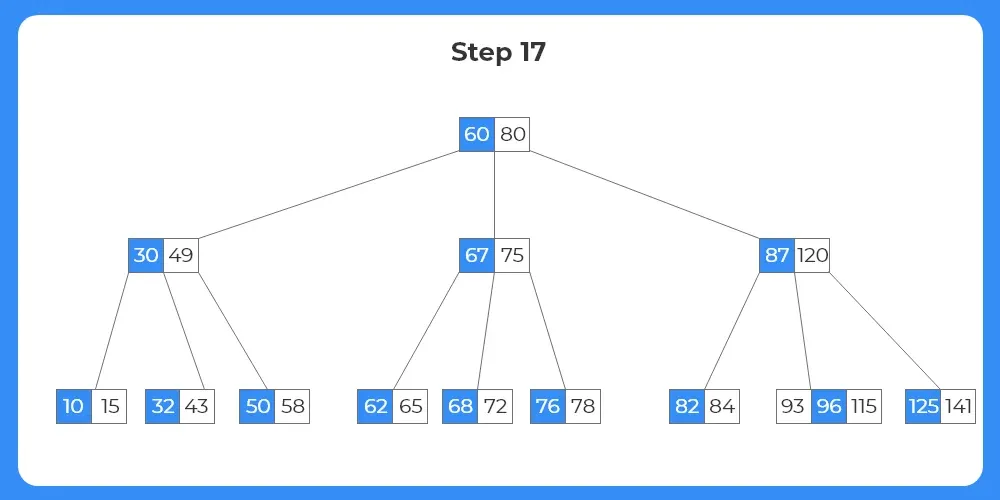
B Tree - Deletion

C Code For Deletion In B-Tree

Run 
// Deleting a key from a B-tree in C

#include <stdio.h>
#include <stdlib.h>

#define MAX 3
#define MIN 2

struct BTreeNode
{
  int item[MAX + 1], count;
  struct BTreeNode *linker[MAX + 1];
};

struct BTreeNode *root;

// Node creation
struct BTreeNode *createNode (int item, struct BTreeNode *child)
{
  struct BTreeNode *newNode;
  newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  newNode->item[1] = item;
  newNode->count = 1;
  newNode->linker[0] = root;
  newNode->linker[1] = child;
  return newNode;
}

// Add value to the node
void addValToNode (int item, int pos, struct BTreeNode *node,
	      struct BTreeNode *child)
{
  int j = node->count;
  while (j > pos)
    {
      node->item[j + 1] = node->item[j];
      node->linker[j + 1] = node->linker[j];
      j--;
    }
  node->item[j + 1] = item;
  node->linker[j + 1] = child;
  node->count++;
}

// Split the node
void splitNode (int item, int *pval, int pos, struct BTreeNode *node,
	   struct BTreeNode *child, struct BTreeNode **newNode)
{
  int median, j;

  if (pos > MIN)
    median = MIN + 1;
  else
    median = MIN;

  *newNode = (struct BTreeNode *) malloc (sizeof (struct BTreeNode));
  j = median + 1;
  while (j <= MAX)
    {
      (*newNode)->item[j - median] = node->item[j];
      (*newNode)->linker[j - median] = node->linker[j];
      j++;
    }
  node->count = median;
  (*newNode)->count = MAX - median;

  if (pos <= MIN)
    {
      addValToNode (item, pos, node, child);
    }
  else
    {
      addValToNode (item, pos - median, *newNode, child);
    }
  *pval = node->item[node->count];
  (*newNode)->linker[0] = node->linker[node->count];
  node->count--;
}

// Set the value in the node
int setValueInNode (int item, int *pval,
		struct BTreeNode *node, struct BTreeNode **child)
{
  int pos;
  if (!node)
    {
      *pval = item;
      *child = NULL;
      return 1;
    }

  if (item < node->item[1])
    {
      pos = 0;
    }
  else
    {
      for (pos = node->count; (item < node->item[pos] && pos > 1); pos--)
	;
      if (item == node->item[pos])
	{
	  printf ("Duplicates not allowed\n");
	  return 0;
	}
    }
  if (setValueInNode (item, pval, node->linker[pos], child))
    {
      if (node->count < MAX)
	{
	  addValToNode (*pval, pos, node, *child);
	}
      else
	{
	  splitNode (*pval, pval, pos, node, *child, child);
	  return 1;
	}
    }
  return 0;
}

// Insertion operation
void insertion (int item)
{
  int flag, i;
  struct BTreeNode *child;

  flag = setValueInNode (item, &i, root, &child);
  if (flag)
    root = createNode (i, child);
}

// Copy the successor
void copySuccessor (struct BTreeNode *myNode, int pos)
{
  struct BTreeNode *dummy;
  dummy = myNode->linker[pos];

  for (; dummy->linker[0] != NULL;)
    dummy = dummy->linker[0];
  myNode->item[pos] = dummy->item[1];
}

// Remove the value
void removeVal (struct BTreeNode *myNode, int pos)
{
  int i = pos + 1;
  while (i <= myNode->count)
    {
      myNode->item[i - 1] = myNode->item[i];
      myNode->linker[i - 1] = myNode->linker[i];
      i++;
    }
  myNode->count--;
}

// Do right shift
void rightShift (struct BTreeNode *myNode, int pos)
{
  struct BTreeNode *x = myNode->linker[pos];
  int j = x->count;

  while (j > 0)
    {
      x->item[j + 1] = x->item[j];
      x->linker[j + 1] = x->linker[j];
    }
  x->item[1] = myNode->item[pos];
  x->linker[1] = x->linker[0];
  x->count++;

  x = myNode->linker[pos - 1];
  myNode->item[pos] = x->item[x->count];
  myNode->linker[pos] = x->linker[x->count];
  x->count--;
  return;
}

// Do left shift
void leftShift (struct BTreeNode *myNode, int pos)
{
  int j = 1;
  struct BTreeNode *x = myNode->linker[pos - 1];

  x->count++;
  x->item[x->count] = myNode->item[pos];
  x->linker[x->count] = myNode->linker[pos]->linker[0];

  x = myNode->linker[pos];
  myNode->item[pos] = x->item[1];
  x->linker[0] = x->linker[1];
  x->count--;

  while (j <= x->count)
    {
      x->item[j] = x->item[j + 1];
      x->linker[j] = x->linker[j + 1];
      j++;
    }
  return;
}

// Merge the nodes
void mergeNodes (struct BTreeNode *myNode, int pos)
{
  int j = 1;
  struct BTreeNode *x1 = myNode->linker[pos], *x2 = myNode->linker[pos - 1];

  x2->count++;
  x2->item[x2->count] = myNode->item[pos];
  x2->linker[x2->count] = myNode->linker[0];

  while (j <= x1->count)
    {
      x2->count++;
      x2->item[x2->count] = x1->item[j];
      x2->linker[x2->count] = x1->linker[j];
      j++;
    }

  j = pos;
  while (j < myNode->count)
    {
      myNode->item[j] = myNode->item[j + 1];
      myNode->linker[j] = myNode->linker[j + 1];
      j++;
    }
  myNode->count--;
  free (x1);
}

// Adjust the node
void adjustNode (struct BTreeNode *myNode, int pos)
{
  if (!pos)
    {
      if (myNode->linker[1]->count > MIN)
	{
	  leftShift (myNode, 1);
	}
      else
	{
	  mergeNodes (myNode, 1);
	}
    }
  else
    {
      if (myNode->count != pos)
	{
	  if (myNode->linker[pos - 1]->count > MIN)
	    {
	      rightShift (myNode, pos);
	    }
	  else
	    {
	      if (myNode->linker[pos + 1]->count > MIN)
		{
		  leftShift (myNode, pos + 1);
		}
	      else
		{
		  mergeNodes (myNode, pos);
		}
	    }
	}
      else
	{
	  if (myNode->linker[pos - 1]->count > MIN)
	    rightShift (myNode, pos);
	  else
	    mergeNodes (myNode, pos);
	}
    }
}

// Delete a value from the node
int delValFromNode (int item, struct BTreeNode *myNode)
{
  int pos, flag = 0;
  if (myNode)
    {
      if (item < myNode->item[1])
	{
	  pos = 0;
	  flag = 0;
	}
      else
	{
	  for (pos = myNode->count; (item < myNode->item[pos] && pos > 1);
	       pos--)
	    ;
	  if (item == myNode->item[pos])
	    {
	      flag = 1;
	    }
	  else
	    {
	      flag = 0;
	    }
	}
      if (flag)
	{
	  if (myNode->linker[pos - 1])
	    {
	      copySuccessor (myNode, pos);
	      flag = delValFromNode (myNode->item[pos], myNode->linker[pos]);
	      if (flag == 0)
		{
		  printf ("Given data is not present in B-Tree\n");
		}
	    }
	  else
	    {
	      removeVal (myNode, pos);
	    }
	}
      else
	{
	  flag = delValFromNode (item, myNode->linker[pos]);
	}
      if (myNode->linker[pos])
	{
	  if (myNode->linker[pos]->count < MIN)
	    adjustNode (myNode, pos);
	}
    }
  return flag;
}

// Delete operaiton
void delete (int item, struct BTreeNode *myNode)
{
  struct BTreeNode *tmp;
  if (!delValFromNode (item, myNode))
    {
      printf ("Not present\n");
      return;
    }
  else
    {
      if (myNode->count == 0)
	{
	  tmp = myNode;
	  myNode = myNode->linker[0];
	  free (tmp);
	}
    }
  root = myNode;
  return;
}

void searching (int item, int *pos, struct BTreeNode *myNode)
{
  if (!myNode)
    {
      return;
    }

  if (item < myNode->item[1])
    {
      *pos = 0;
    }
  else
    {
      for (*pos = myNode->count;
	   (item < myNode->item[*pos] && *pos > 1); (*pos)--)
	;
      if (item == myNode->item[*pos])
	{
	  printf ("%d present in B-tree", item);
	  return;
	}
    }
  searching (item, pos, myNode->linker[*pos]);
  return;
}

void traversal (struct BTreeNode *myNode)
{
  int i;
  if (myNode)
    {
      for (i = 0; i < myNode->count; i++)
	{
	  traversal (myNode->linker[i]);
	  printf ("%d ", myNode->item[i + 1]);
	}
      traversal (myNode->linker[i]);
    }
}

int main ()
{
  int item, ch;

  insertion (8);
  insertion (9);
  insertion (10);
  insertion (11);
  insertion (15);
  insertion (16);
  insertion (17);
  insertion (18);
  insertion (20);
  insertion (23);

  traversal (root);

  delete (20, root);
  printf ("\n");
  traversal (root);
}

Output:

8 9 10 11 15 16 17 18 20 23 
8 9 10 11 15 16 17 18 23 8 9

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java