Binary Search Tree: Insertion

March 1, 2023

Insertion in a Binary Search Tree

Binary Search tree is fairly easy and we just need to know a few simple rules given below –

Binary Search Tree Insertion

Rules for Insertion in a Binary Search Tree (BST)

  • The left subtree for any given node will only contain nodes which are lesser than the current node
  • The right subtree for any given node will only contain nodes which are greater than the current node
  • Each subtree must also follow the above rules of BST

Pre Requisite to Insertion

Binary Search Tree_ Insertion 1

So, first, we will learn how to search a given node(value), in a binary search tree

Searching in a Binary Search Tree

Let us say we want to 9 in the binary search tree given in our example above, what approach we would follow?

Algorithm

  • Start from the root node
  • Compare the value with the root node, if same then found, return True
  • If the value is less than the root node, recurse to the left node. Else recurse to the right node
  • Do this recursively, until the value is found or not found

Example

Assuming we want to find 9 in the above example

  1. The root node is 15, (9 <15) thus recursing to the left node
  2. Now, the left node is 13, (9<14) thus again, recursing to the left node
  3. Now, the left node is 8, (9>8) thus, recursing to the right node
  4. Finally, the right node is 9, (9=9), thus value found, return true

Code to implement Search

// A sample C function to check if a given node exists in a binary search tree or not
struct node* search(struct node* root, int value) 
{ 
    // Check if the root is null or value is present at root itself
    if (root == NULL || root->value == value) 
       return root;

    // Root is smaller than value, go to right subtree's node, doing recusion here
    if (root->value < value) 
       return search(root->right, value); 

    // else only one case is left
    // i.e. Root is greater than value, go to left subtree's node, doing recusion here
    return search(root->left, value); 
}
DSA desktop gif
DSA mobile gif

Priority Queue in C

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Inorder Tree Traversal without Recursion

Preorder Tree Traversal without Recursion

Insertion in a Binary Search Tree

Insertion is fairly simple if you understood search perfectly

  • Try to search the BST for the node to be inserted
  • As the node wouldn’t exist we will hit the leaf node, with null as child node right!
  • Insert the new node here
  • Voila! Party, you’ve inserted

Code for Binary Search Tree Insertion

Run 
// PrepInsta's program to do insertion in a Binary Search Tree (BST)
#include<stdio.h> 
#include<stdlib.h>

// Basic struct of Tree 
struct node 
{ 
    int val; 
    struct node *left, *right; 
}; 
   
// Function to create a new Node
struct node* newNode(int item) 
{ 
    struct node* temp =  (struct node *)malloc(sizeof(struct node)); 
    temp->val = item; 
    temp->left = temp->right = NULL; 
    return temp; 
} 
   
// Function print the node in inorder format, when insertion is complete
void inorder(struct node* root) 
{ 
    if (root != NULL) 
    { 
        inorder(root->left); 
        printf("%d \n", root->val); 
        inorder(root->right); 
    } 
} 
   
// Here we are finding where to insert the new node so BST is followed
struct node* insert(struct node* node, int val) 
{ 
    /* If the tree(subtree) is empty, return a new node by calling newNode func.*/
    if (node == NULL) return newNode(val); 
  
    /* Else, we will do recursion down the tree to further subtrees */
    if (val < node->val) 
        node->left  = insert(node->left, val); 
    else if (val > node->val) 
        node->right = insert(node->right, val);    
  
    /* (Safety) return the node's pointer which is unchanged */
    return node; 
} 
   
int main() 
{ 
    /* Our BST will look like this 
              100 
           /     \ 
          40      140 
         /  \    /  \ 
       40   80  120  160 */
    struct node* root = NULL; 
    root = insert(root, 100); 
    insert(root, 60); 
    insert(root, 40); 
    insert(root, 80); 
    insert(root, 140); 
    insert(root, 120); 
    insert(root, 160);
    
   
    // Finally printing the tree using inorder
    inorder(root); 
   
    return 0; 
}

Output:

40 
60 
80 
100 
120 
140 
160

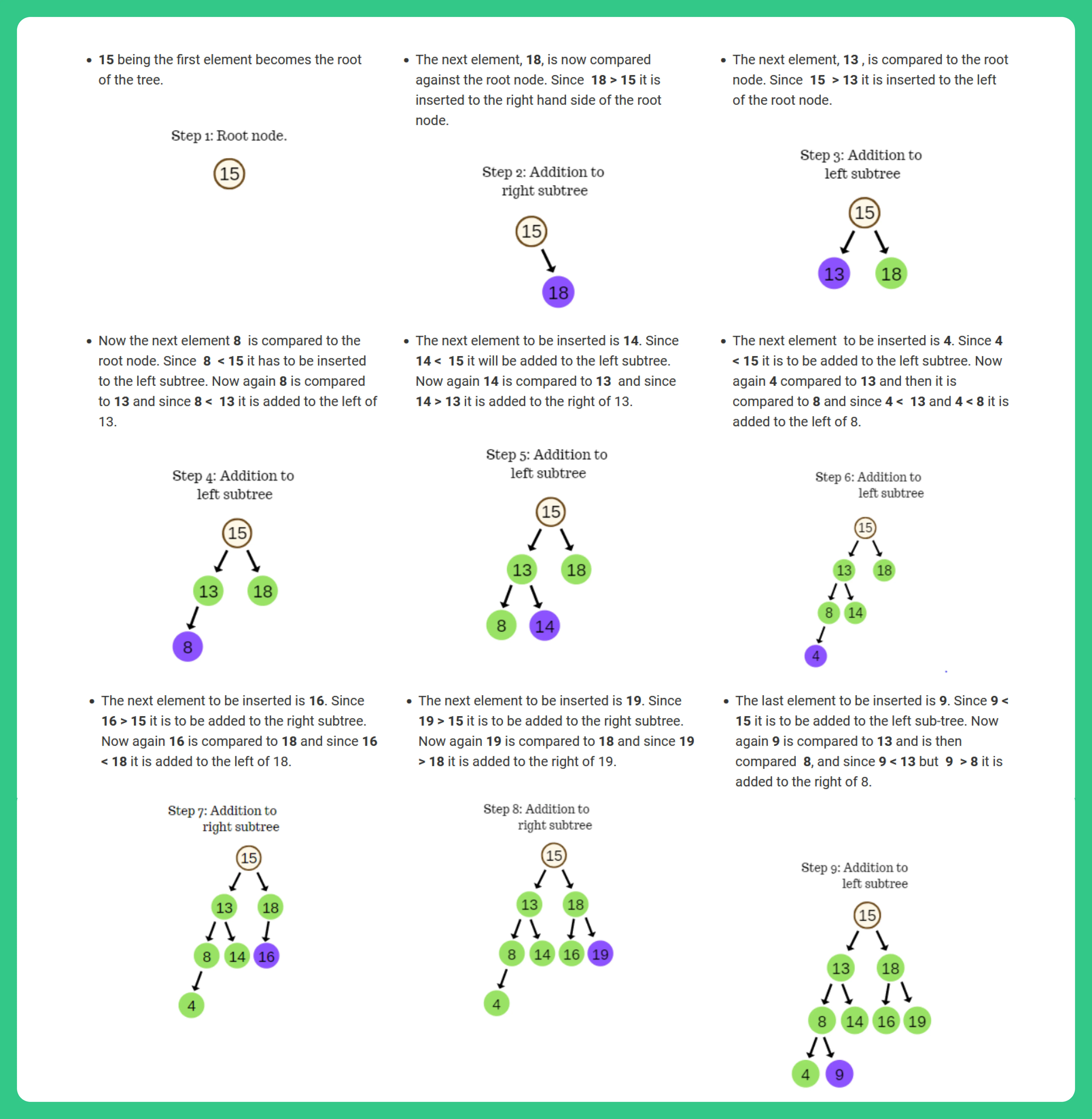
How it works?

  • In binary search trees, we use the INSERT function to add a new element in a tree.
  • Insertion is similar to searching wherein, we first check if the element is present in the given data or not. If not, the node is entered at that position.
  • If the data to be added is greater than the parent data node it is inserted towards the right of the parent; else it is inserted to the left of the parent.
  • In other words,
  • If  root > node, 

then the data node is added to the left sub-tree.

  • If  root < node, 

then the data node is added to the right sub-tree.

For Example: [15, 18, 13, 8, 14, 4, 16, 19, 9]

Binary Search Tree_ Insertion

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java