AVL Tree: Deletion
C Program For Deletion In AVL Tree:
On this page we will discuss about Deletion In AVL Tree in C . AVL tree is self balancing tree in which for all nodes, the difference of height between the left subtree and the right subtree is less than or equal to 1. In this article, an avl tree is created and the difference of height is printed for each node.

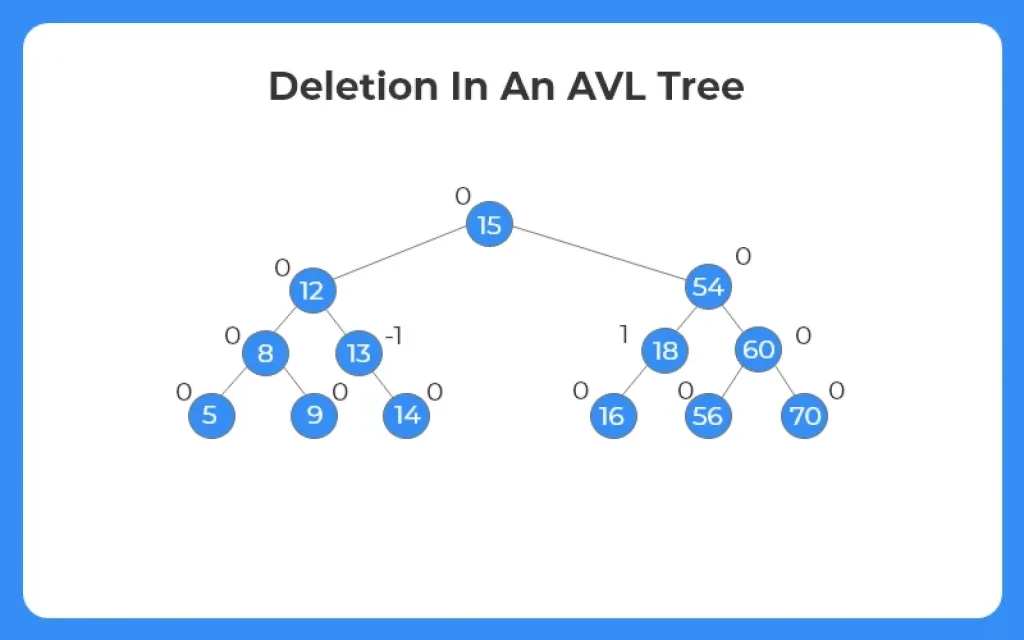
Deletion in an AVL Tree
- Deletion in an AVL tree is similar to that in a BST.
- Deletion of a node tends to disturb the balance factor. Thus to balance the tree, we again use the Rotation mechanism.
- Deletion in AVL tree consists of two steps:
- Removal of the node: The given node is removed from the tree structure. The node to be removed can either be a leaf or an internal node.
- Re-balancing of the tree: The elimination of a node from the tree can cause disturbance to the balance factor of certain nodes. Thus it is important to re- balance theb_fact of the nodes; since the balance factor is the primary aspect that ensures the tree is an AVL Tree.
- If the node to be deleted is a leaf node, it is simply removed from the tree.
- If the node to be deleted has one child node, the child node is replaced with the node to be deleted simply.
- If the node to be deleted has two child nodes then,
- Either replace the node with it’s inorder predecessor , i.e, the largest element of the left sub tree.
- Or replace the node with it’s inorder successor , i.e, the smallest element of the right sub tree.
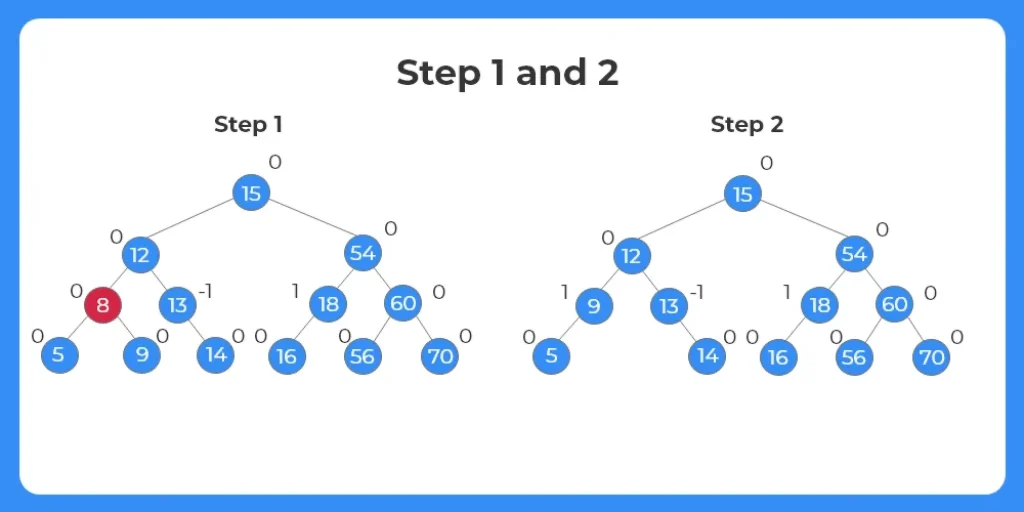
Step 1:
- The node to be deleted from the tree is 8.
- If we observe it is the parent node of the node 5 and 9.
- Since the node 8 has two children it can be replaced by either of it’s child nodes.
Step 2:
- The node 8 is deleted from the tree.
- As the node is deleted we replace it with either of it’s children nodes.
- Here we replaced the node with the inorder successor , i.e, 9.
- Again we check the balance factor for each node.
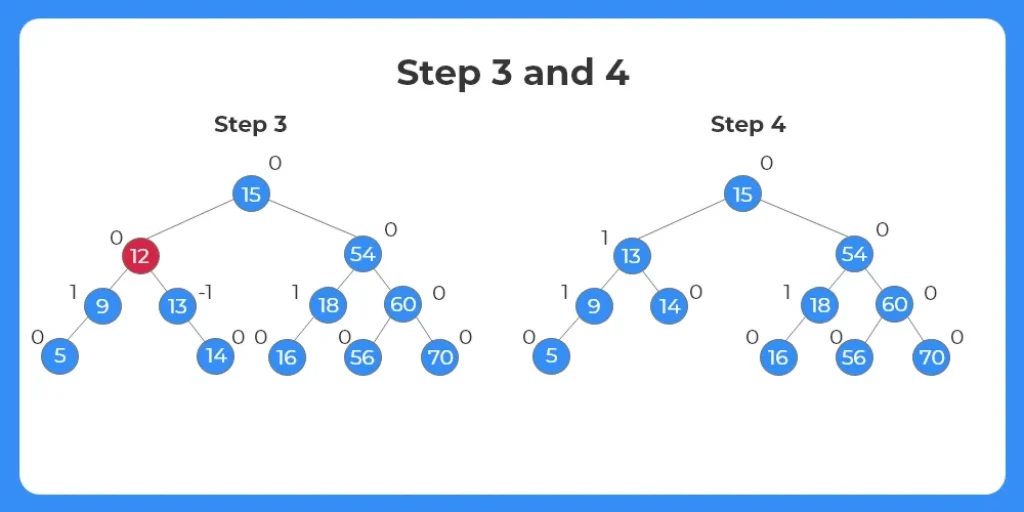
Step 3:
- Now The next element to be deleted is 12.
- If we observe, we can see that the node 12 has a left subtree and a right subtree.
- We again can replace the node by either it’s inorder successor or inorder predecessor.
- In this case we have replaced it by the inorder successor.
Step 4:
- The node 12 is deleted from the tree.
- Since we have replaced the node with the inorder successor, the tree structure looks like shown in the image.
- After removal and replacing check for the balance factor of each node of the tree.
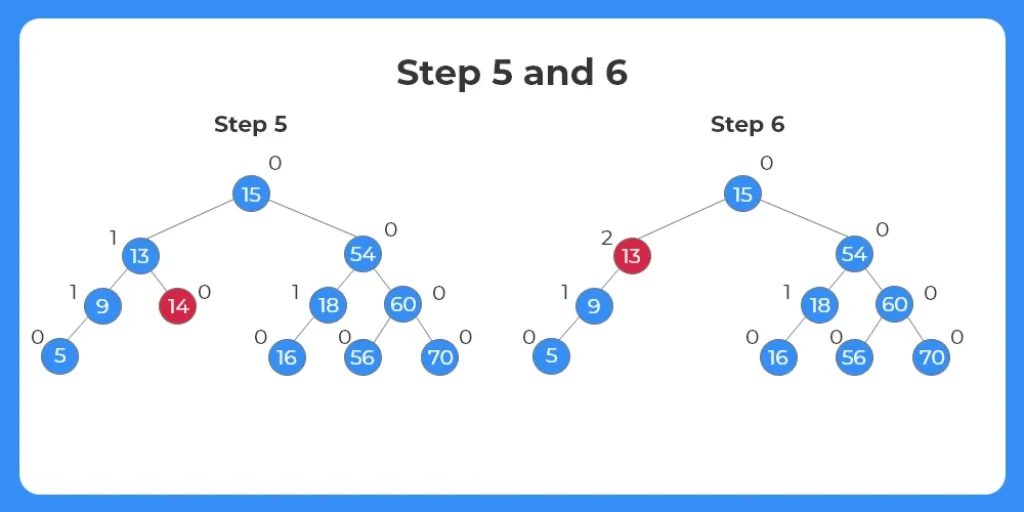
Step 5:
- The next node to be eliminated is 14.
- It can be seen clearly in the image that 14 is a leaf node.
- Thus it can be eliminated easily from the tree.
Step 6:
- As the node 14 is deleted, we check the balance factor of all the nodes.
- We can see the balance factor of the node 13 is 2.
- This violates the terms of the AVL tree thus we need to balance it using the rotation mechanism.
Prime Course Trailer
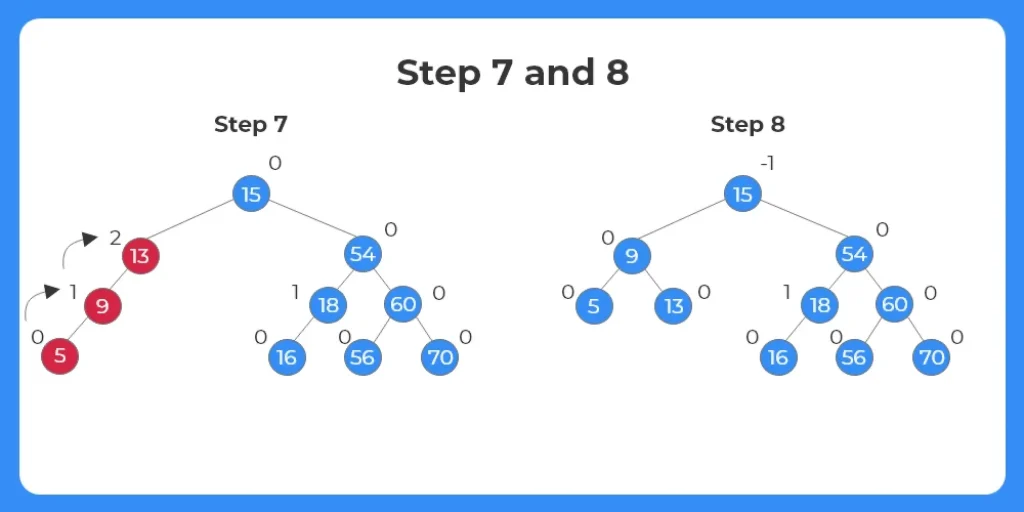
Step 7:
- In order to balance the tree, we identify the rotation mechanism to be applied.
- Here we need to use LL Rotation.
- The nodes involved in the rotation is shown as follows.
Step 8:
- The nodes are rotated and the tree satisfies the conditions of an AVL tree.
- The final structure of the tree is shown as follows.
- We can see all the nodes have their balance factor as ‘0’ , ‘1’ and ‘-1’.
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
C Code For Deletion In AVL Tree
Run
// C program to delete a node from AVL Tree
#include<stdio.h>
#include<stdlib.h>
// An AVL tree node
struct Node
{
int key;
struct Node *left;
struct Node *right;
int height;
};
// A utility function to get maximum of two integers
int max(int a, int b);
// A utility function to get height of the tree
int height(struct Node *N)
{
if (N == NULL)
return 0;
return N->height;
}
// A utility function to get maximum of two integers
int max(int a, int b)
{
return (a > b)? a : b;
}
/* Helper function that allocates a new node with the given key and
NULL left and right pointers. */
struct Node* newNode(int key)
{
struct Node* node = (struct Node*)
malloc(sizeof(struct Node));
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1; // new node is initially added at leaf
return(node);
}
// A utility function to right rotate subtree rooted with y
// See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
struct Node *x = y->left;
struct Node *T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left), height(y->right))+1;
x->height = max(height(x->left), height(x->right))+1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x
// See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
struct Node *y = x->right;
struct Node *T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left), height(x->right))+1;
y->height = max(height(y->left), height(y->right))+1;
// Return new root
return y;
}
// Get Balance factor of node N
int getBalance(struct Node *N)
{
if (N == NULL)
return 0;
return height(N->left) - height(N->right);
}
struct Node* insert(struct Node* node, int key)
{
/* 1. Perform the normal BST rotation */
if (node == NULL)
return(newNode(key));
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else // Equal keys not allowed
return node;
/* 2. Update height of this ancestor node */
node->height = 1 + max(height(node->left),
height(node->right));
/* 3. Get the balance factor of this ancestor
node to check whether this node became
unbalanced */
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && key < node->left->key)
return rightRotate(node);
// Right Right Case
if (balance < -1 && key > node->right->key)
return leftRotate(node);
// Left Right Case
if (balance > 1 && key > node->left->key)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
/* return the (unchanged) node pointer */
return node;
}
/* Given a non-empty binary search tree, return the
node with minimum key value found in that tree.
Note that the entire tree does not need to be
searched. */
struct Node * minValueNode(struct Node* node)
{
struct Node* current = node;
/* loop down to find the leftmost leaf */
while (current->left != NULL)
current = current->left;
return current;
}
// Recursive function to delete a node with given key
// from subtree with given root. It returns root of
// the modified subtree.
struct Node* deleteNode(struct Node* root, int key)
{
// STEP 1: PERFORM STANDARD BST DELETE
if (root == NULL)
return root;
// If the key to be deleted is smaller than the
// root's key, then it lies in left subtree
if ( key < root->key )
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the
// root's key, then it lies in right subtree
else if( key > root->key )
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is
// the node to be deleted
else
{
// node with only one child or no child
if( (root->left == NULL) || (root->right == NULL) )
{
struct Node *temp = root->left ? root->left :
root->right;
// No child case
if (temp == NULL)
{
temp = root;
root = NULL;
}
else // One child case
*root = *temp; // Copy the contents of
// the non-empty child
free(temp);
}
else
{
// node with two children: Get the inorder
// successor (smallest in the right subtree)
struct Node* temp = minValueNode(root->right);
// Copy the inorder successor's data to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
}
// If the tree had only one node then return
if (root == NULL)
return root;
// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
root->height = 1 + max(height(root->left),
height(root->right));
// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to
// check whether this node became unbalanced)
int balance = getBalance(root);
// If this node becomes unbalanced, then there are 4 cases
// Left Left Case
if (balance > 1 && getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root->left) < 0) { root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// A utility function to print preorder traversal of
// the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
if(root != NULL)
{
printf("%d ", root->key);
preOrder(root->left);
preOrder(root->right);
}
}
/* Driver program to test above function*/
int main()
{
struct Node *root = NULL;
/* Constructing tree given in the above figure */
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
/* The constructed AVL Tree would be
9
/ \
1 10
/ \ \
0 5 11
/ / \
-1 2 6
*/
printf("Preorder traversal of the constructed AVL "
"tree is \n");
preOrder(root);
root = deleteNode(root, 10);
/* The AVL Tree after deletion of 10
1
/ \
0 9
/ / \
-1 5 11
/ \
2 6
*/
printf("\nPreorder traversal after deletion of 10 \n");
preOrder(root);
return 0;
}
Output:
Preorder traversal of the constructed AVL tree is 9 1 0 -1 5 2 6 10 11 Preorder traversal after deletion of 1 9 2 0 -1 5 6 10 11
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java






Login/Signup to comment