Postorder Tree Traversal in Binary Tree in C

January 11, 2024

Postorder
Direction (Inorder) Anti Clock
Rule Left Right Center (LRC)

Postorder Traversal of the Tree in C

Postorder Tree Traversal in Binary Tree in C is one of the most frequently used tree traversals, in such traversal we try to print the left most root first. Let us see how post order tree traversals work –

Postorder Tree Traversal in Binary Tree in C Language

Working of PostOrder Algorithm

  • We traverse in Anti Clock wise Direction
  • Rule followed is LRC(Left-Right-Center)

Which means that we try to visit the leftmost node of the tree first and then its subtree’s right node and then center/middle node and keep on doing the same iteratively.

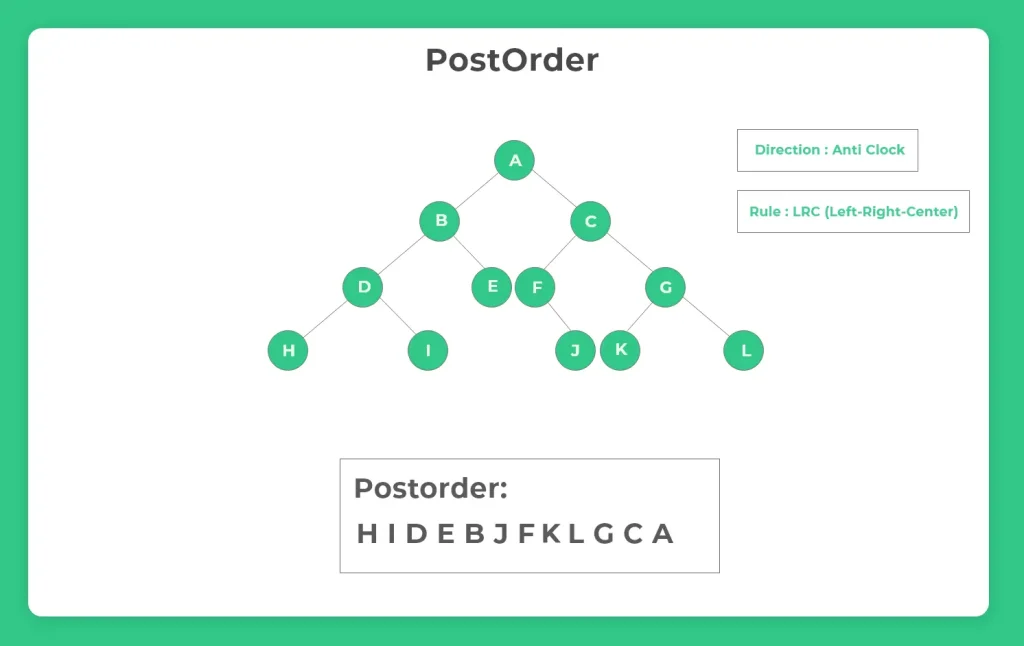
Working for the above image for Postorder traversal

We traverse the tree and try to go to the left most node
  • Here, Leftmost item is 8, right item : 9, middle item : 4 (Now recursive moving in the tree)
    • Print 8 9 4
  • Leftmost item is 4 (However, we’ve visited it already), so now, right item is 5 then middle item : 2
    • Print 5 2
  • The left side of the tree is done, moving to right side of the tree
  • (In right subtree) The leftmost item: NULL, and its right item is: 10, middle item: 10 (Move up the tree)
    • Print 10 6
  • Central item, 3, however 3 has child elements, so we try to visit its subtree’s
  • Now, we come across 7, which still has a subtree so we recur down the tree
  • The left node of 7 is last node in the tree and left most, its right sibling: 12, middle: 7
    • Print: 11 12 7
  • Now, recurring up, whole subtree (Both left & right of 3 is printed so
    • Print 4

Algorithm for Postorder Traversal

Postorder(root)
  • Traverse the left sub-tree, (recursively call postorder(root -> left).
  • Traverse the right sub-tree, (recursively call postorder(root -> right).
  • Visit and print the root node.
DSA desktop gif
DSA mobile gif

Priority Queue in C

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Preorder Tree Traversal without Recursion

Postorder Tree Traversal without Recursion

Run 
// Program for tree traversal postorder in Binary Tree
#include<stdio.h>
#include<stdlib.h>
// We are creating struct for the binary tree below
struct node
{
  int data;
  struct node *left, *right;
};

// newNode function for initialisation of the newly created node
struct node *newNode (int item)
{
  struct node *temporary = (struct node *) malloc (sizeof (struct node));
  temporary->data = item;
  temporary->left = temporary->right = NULL;
  return temporary;
}

// Here we print the postorder recursively
void postorder (struct node *root)
{
  if (root != NULL)
    {
      postorder (root->left);
      postorder (root->right);
      printf ("%d ", root->data);
    }
}

// Basic Program to insert new node at the correct position in BST
struct node *insert (struct node *node, int data)
{
  /* When there no node in the tree(subtree) then create 
   and return new node using newNode function */
  if (node == NULL)
    return newNode (data);

  /* If not then we recur down the tree to find correct position for insertion */
  if (data < node->data)
    node->left = insert (node->left, data);
  else if (data > node->data)
    node->right = insert (node->right, data);

  return node;
}

int main ()
{
  /* What our binary search tree looks like really 
      9 
     / \ 
    7  14
   / \ / \ 
  5  8 11 16 */
  
  struct node *root = NULL;
  root = insert (root, 9);
  insert (root, 7);
  insert (root, 5);
  insert (root, 8);
  insert (root, 14);
  insert (root, 11);
  insert (root, 16);

  printf ("The postorder is :\n");
  postorder (root);

  return 0;
}

Output:

The postorder is :
5 8 7 11 16 14 9

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java