Postorder Tree Traversal In Binary Tree In C++

March 2, 2023

Postorder Tree Traversal

Postorder traversal is a depth first algorithm. There are three types of traversals in tree: Preorder, Inorder, Postorder. In this article, postorder tree traversal is performed using recursion.

Postorder tree traversal in binary tree in Cpp

More About Postorder Traversal:

  1. In postorder traversal, we first move to the left subtree then to the right subtree and finally print the node.
  2. Used when we want to free the nodes of the tree.
  3. It is also used to find the postfix expression.
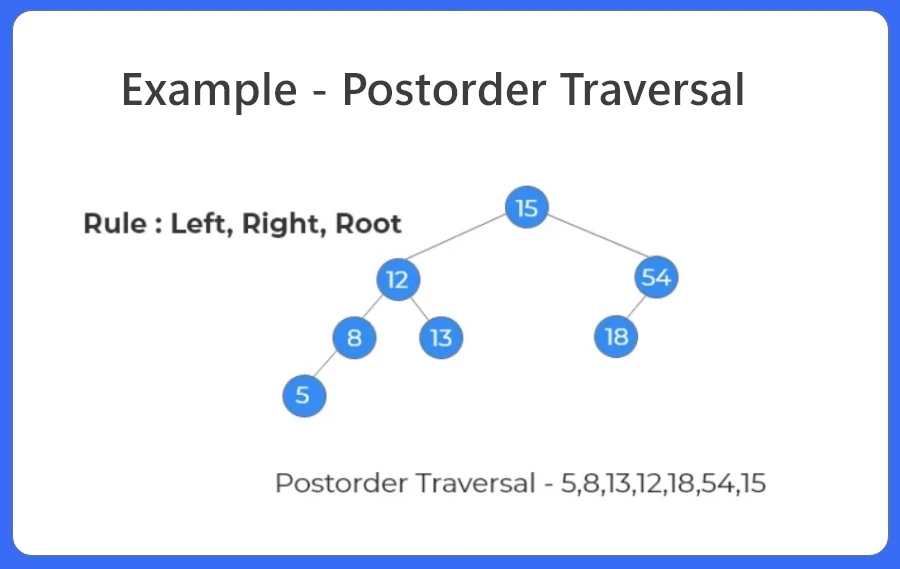
postorder-tree-traversal-in-binary-tree

Steps To Find Postorder Traversal:

  1. Traverse the left subtree. Print the leftmost node ie 5.
  2. Move back, traverse the right subtree.
  3. Since there is no right subtree, 8 is printed.
  4. 13 is printed and the parent node is printed which is 12.
  5. Finally move, to the right subtree.
  6. 18 and 54 are printed.
  7. Print the root.

 

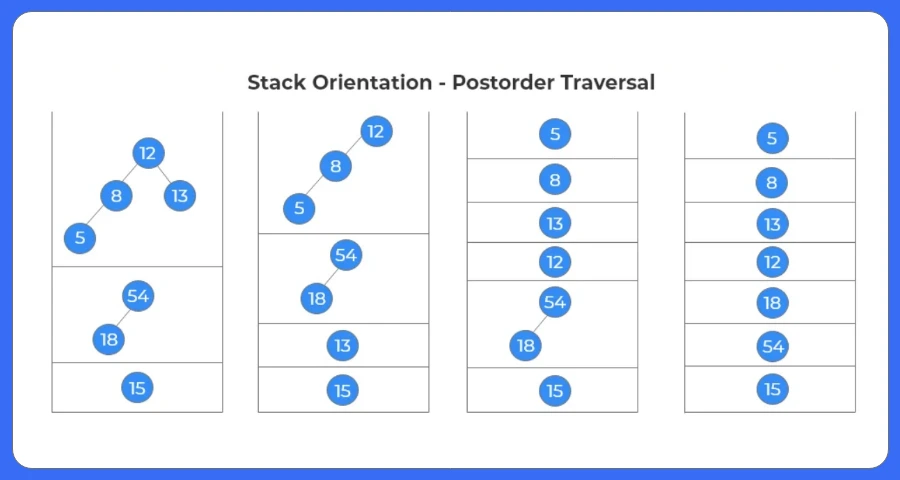
Postorder tree traversal in binary tree in Cpp
DSA desktop gif
DSA mobile gif

Trees in Data Structure(Introduction)

Types of Trees in data structure

Inorder Postorder Preorder Traversal Examples

Inorder Tree Traversal in Binary Tree

Preorder Tree Traversal in Binary Tree

Algorithm To Find Postorder Traversal:

  1. If root is NULL, return.
  2. Visit the left subtree.
  3. Visit the right subtree.
  4. Print the node.

Code Implementation for Preorder Tree traversal

Run 
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};
void postorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Visit Left subtree
  postorder_traversal (root->left);
  // Visit right subtree
  postorder_traversal (root->right);
  // Print the data
  cout << root->data << " ";
}

int main ()
{
  Tree *root = new Tree (15);
  root->left = new Tree (12);
  root->right = new Tree (54);
  root->left->left = new Tree (8);
  root->left->right = new Tree (13);
  root->left->left->left = new Tree (5);
  root->right->left = new Tree (18);
  postorder_traversal (root);
  return 0;
}


Output:

5 8 13 12 18 54 15

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Stacks

  • Introduction to Stack in Data Structure
    Click Here
  • Operations on a Stack
    Click Here
  • Stack: Infix, Prefix and Postfix conversions
    Click Here
  • Stack Representation in –
    C | C++ | Java
  • Representation of a Stack as an Array. –
    C | C++ | Java
  • Representation of a Stack as a Linked List. –
    C | C++ | Java
  • Infix to Postfix Conversion –
    C | C++ | Java
  • Infix to prefix conversion in –
    C | C++ | Java
  • Postfix to Prefix Conversion in –
    C | C++ | Java

Queues

  • Queues in Data Structures (Introduction)
    Click Here
  • Queues Program in C and implementation
    Click Here
  • Implementation of Queues using Arrays | C Program
    Click Here
  • Types of Queues in Data Structure
    Click Here
  • Application of Queue Data Structure
    Click Here
  • Insertion in Queues Program (Enqueuing) –
    C | C++ | Java
  • Deletion (Removal) in Queues Program(Dequeuing) –
    C | C++ | Java
  • Reverse a Queue –
    C | C++ | Java
  • Queues using Linked Lists –
    C | C++ | Java
  • Implement Queue using Stack –
    C | C++ | Java
  • Implement Queue using two Stacks –
    C | C++ | Java

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction –
    C | C++ | Java
  • Priority Queue Implementation using Array –
    C | C++ | Java
  • Priority Queue using Linked List –
    C | C++ | Java
  • Priority Queue Insertion and Deletion-
    C | C++ | Java

Stacks

Queues

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction – C | C++ | Java
  • Priority Queue Implementation using Array – C | C++ | Java
  • Priority Queue using Linked List – C | C++ | Java
  • Priority Queue Insertion and Deletion- C | C++ | Java

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout