Trees in Data Structures (Introduction)
Trees in Data Structures
A tree is a hierarchical data structure, which has one root node and multiple child nodes(branches). Unlike, Arrays, Linked Lists, Stacks or queues, a Tree is non linear data structure.
Classification of Trees
Trees are classified by the following types –
- By Max number of branches – Binary, Ternary, n-ary
- By Heights of subtree – Full, complete, perfect, balanced (Check this page)
The following diagram shows one example of each –
- Binary Tree: A tree where each node can have a maximum of two child nodes
- Ternary Tree: A tree where each node can have a maximum of three child nodes
- n-ary Tree: A tree where each node can have a maximum of n child nodes
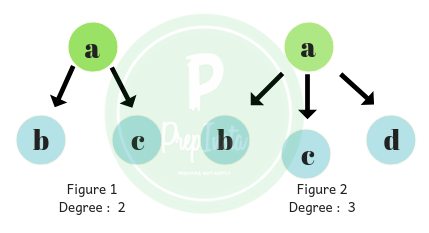
This n value is sometimes called as the degree of the tree.
Why Trees?
Hierarchical approach
- One reason could be that we want to store information that follows, natural hierarchy, like how we store folders in a computer system.
No Upper Limit
- Trees, unlike arrays, stacks, queues do not have an upper limit on how many nodes can be created, as they are created using pointers
Quicker Search and Access
- Trees (BST) are able to do searching quicker than arrays, linked lists etc
Moderate Insertion/Deletion
- Trees provide moderate insertion/deletion (Slower than Linked lists, quicker than arrays)
Technical Description of Trees
- Trees can defined as a collection of entities, that constitute it’s frame, known as nodes.
- Nodes are the basic building blocks of a tree structure that store some data/value .
These are ADT (Abstract Data Structures) which form a hierarchical layout comprising of a single root node followed by parent nodes and children nodes, which are connected to each other via edges.
Since trees are flexible and powerful data structures, they are multipurpose data structure that provide a wide range of applications to the user.
Components
- Root
- Parent
- Child nodes
- Siblings
- Leaves
- Brach
- Sub-Tree
- Ancestor
- Descendants
- Null Nodes
others
- Degree
- Edges
- Path
- Depth
- Level
- Height
1. Root
- The topmost node of a tree is known as the root.
- There exists only one root node per tree.
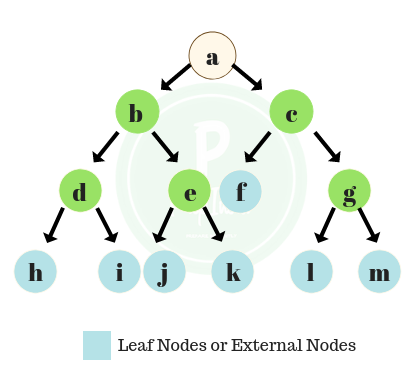
- Taking the image above as reference, node ‘a’ is the root of the tree as shown here.
2. Parent
- Any node which has an edge directed downwards to the child node is known as parent node.
- Each parent can have one or more child node.
- In the given image we can see, the node ‘a’ is the parent of the nodes ‘b’ and ‘c’.
3. Child Node
- Any node which has an edge directed upwards to the parent node is known as child node.
- Each child node has a single parent node.
- In the given image we can see, the nodes ‘h’ and ‘i’ are the child nodes of the node ‘d’.
4. Sibling
- A set of nodes that are extended from the same parent are known as the siblings.
- In the given image, we can see that
- the nodes ‘b’ and ‘c’ are sibling nodes.
- the nodes ‘h’ and ‘i’ are sibling nodes.
5. Leaf(external nodes)
- Any node that does not have any child node is known as the leaf node.
- In the given image, the nodes ‘f’, ‘h’, ‘i’, ‘j’, ‘k’, ‘l’ and ‘m’ are leaf nodes since these nodes are terminal and have no further child nodes.
Total Number of leaf nodes in a Binary Tree = Total Number of nodes with 2 children + 1
6. Branch(internal nodes)
- Any node which has at least one child node is known as branch node.
- In the given image, the nodes ‘b’ , ‘c’ , ‘d’ , ‘e’ , ‘g’ are branch nodes since each of these nodes extend further to their respective children.
7. Sub-Tree
- A sub tree of a tree is defined as a tree that consist of a node along with all it’s descendants.
- In the image , we can see that a sub tree can be extended from node ‘b’ which will be termed as the left sub tree.
- Similarly, a sub tree can be extended from the node ‘c’ which will be termed as the right sub tree.
8. Ancestor
- Any predecessor of a node along with all the ancestors of the predecessor of that node is known is as the ancestor.
- The root node has no ancestors.
- In the given image, the ancestors of the node ‘h’ will be ‘d’, ‘b’ and ‘a’.
9. Descendant
- All the children of a node along with all the descendants of the children of a node is known as descendant.
- A leaf node has no descendants.
- In the given image, if we consider the node ‘c’, the descendants of node ‘c’ will be nodes ‘f’ , ‘g’ , ‘l’ and ‘m’ .
10. Null Nodes
- If in a binary tree, a node has only one child it is said to have a single null link.
- Similarly if a node has no child node it is said to have two null links.
- We can see in the image given the two cases of null links.
Terminologies
1. Degree.
- The degree of a node can be defined as it’s number of sub trees.
- A node with zero degree is a leaf node.
- A node with maximum degree is the root node in the tree.
2. Edge
- An edge can be defined as a connection or a link from one node to another node.
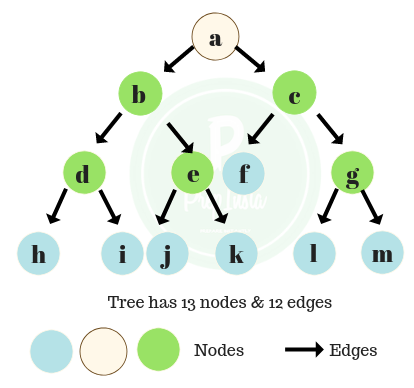
- In the given image, we have 3 edges from node ‘a’ to node ‘h’.
- If we see the image, we can see clearly that we have a total of 13 nodes and 12 edges.
- Thus, we can say that ,
No. of edges = No. of nodes – 1
3. Path
- A course of nodes and edges for operations such as traversal,etc is known as a path.
- Let us see with the help of an example taking the image as reference,
- The path from node ‘a’ to the node ‘h’ is represented in red which consist of 4 nodes and 3 edges.
- Similarly, the path from node ‘a’ to ‘l’ is represented in purple which consist of 4 nodes and 3 edges.
4. Depth
- The number of edges that lie in between the path from a node to the root in a tree is defined as the depth of the tree.
- In the image given here, we can see the depth of each node. For instance the depth of the root node is zero.
5. Level
- Level of a node is symbolic of the generation of a given node. It is one greater than the level of it’s parent.
- For instance, in the given image we can see, the level of the node ‘b’ and ‘c’ is one more than the level of their parent node ‘a’.
Very Important
Some articles say the level of the tree starts from 0 and some say 1. Actually the correct answer is 1. Depth of tree starts from 0 and the level starts from 1.
But, still, you need to know formulas for both and depending on the question and options, you need to choose the correct one. Most MCQ will say like this - Assume Level of tree starts from 0.
But, still, you need to know formulas for both and depending on the question and options, you need to choose the correct one. Most MCQ will say like this - Assume Level of tree starts from 0.
Note – Formula Max number of nodes at any given level for the tree would be
- 2L (If level Starts from 0)
- 2L-1 (If level Starts from 1)
Example (Considering level starts from 1) –
- Level 1 (Max nodes) =21-1 = 1
- Level 2 (Max nodes) =22-1= 2
- Level 3 (Max nodes) =23-1= 4
- Level 4 (Max nodes) =24-1= 8
Thus max possible nodes in the tree for Level 4 would be
- 21-1 + 22-1 + 23-1 + 24-1 = 1 + 2 + 4 + 8 = 15
This above can be generalised to a formula as :
Maximum number of nodes (Considering Level Starts from 1) =
- 1 + 2 + 4 + 8 + … + 2L-1 = (2L – 1)
The above formula will change to (2L+1 – 1) (If level starts from 0)
Formula summary
Formula Max number of nodes at any given level for the tree would be:
Formula Max number of nodes in the whole tree would be:
Formula Max number of nodes at any given level for the tree would be:
- 2L (If level Starts from 0)
- 2L-1 (If level Starts from 1)
Formula Max number of nodes in the whole tree would be:
- 2L+1 -1 (If level Starts from 0)
- 2L - 1 (If level Starts from 1)
6. Height
- Height of a node can be defined as the longest path downwards between the root node and a leaf.
- For example in the given image, we can see that the height of the node ‘l’ is 3; since the distance between it and the root node is 3.
- Height of a tree starts from 0
Very Important
Some articles say the height of the tree starts from 0 and some say 1. Actually the correct answer is 0.
The definition of height is: Height of a node can be defined as the longest path downwards between the root and a leaf.
Clearly, if a tree has only root node then root and leaf are same and distance is 0 right?
If an MCQ Question comes in the exam, it will generally say - Assume Height starts from (0 or 1), if not then learn both below formulas safe side mark whichever is present.
The definition of height is: Height of a node can be defined as the longest path downwards between the root and a leaf.
Clearly, if a tree has only root node then root and leaf are same and distance is 0 right?
If an MCQ Question comes in the exam, it will generally say - Assume Height starts from (0 or 1), if not then learn both below formulas safe side mark whichever is present.
Formula –
Height of tree is h then Max nodes a Full Binary Tree will have
- (2h+1 – 1)nodes (if h starts from 0)
- (2h – 1)nodes (if h starts from 1)
Formula – Minimum number of nodes in a Binary Tree of height h would be
- (h + 1) (if h starts from 0)
- h (if h starts from 1)
Formula – In a Binary Tree with N nodes, minimum possible height
- (Log2(N+1) – 1) (if h starts from 0)
- Log2(N+1) (if h starts from 1)
Operations performed on a Tree
- Enumerating.
- Traversing and Searching.
- Insertion.
- Deletion.
Applications of a Tree
The data structure trees and its types come in handy since they provide a wide range of functions; some of which are:
- It provides a simple and systematic method to store and represent the data in a hierarchical form.
- It stores the data/values in a way that provides ease of search and traversal.
- It executes the insertion/deletion operation within a moderate range of time.
- A certain category of trees(,i.e, B- Tree,etc.) can be used for indexing purposes in database.
- It is used for the representation of ordered lists of data/information.
Login/Signup to comment