Preorder Tree Traversal in Binary Tree In C++

March 3, 2023

Preorder Tree Traversal

Preorder traversal is a depth first algorithm. There are three types of traversals in tree: Preorder, Inorder, Postorder. In this article, preorder tree traversal is performed using recursion.

Preorder Tree Traversal in binary tree in C++

More About Preorder Traversal

  1. We first print the value of the node,them move to the left subtree and finally to the right subtree.
  2. If we need to explore more about the node itself before inspecting its leaves, we use preorder traversal.
  3. Preorder traversal is used to find the prefix expression of an expression tree.
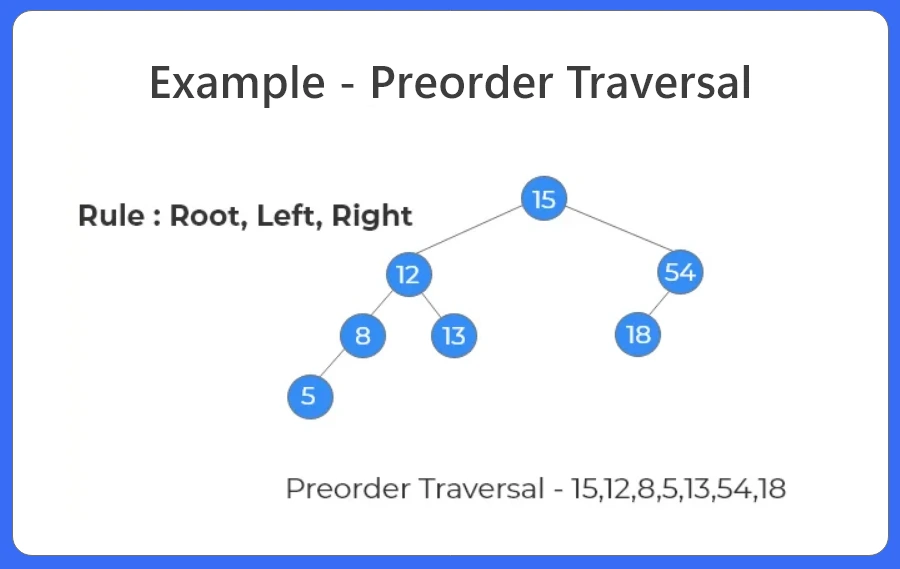
Preorder Tree Traversal in binary tree in C++

Steps To Find Preorder Traversal:

  1. Print the root node and traverse the left subtree.
  2. After printing 12, move to the left.
  3. 8 is printed and we move to the left subtree.
  4. Print 5 and move back,
  5. Since there is only 1 right child 13 is printed and we move to the right subtree.
  6. 54 and 18 are printed.
DSA desktop gif
DSA mobile gif

Trees in Data Structure(Introduction)

Types of Trees in data structure

Inorder Postorder Preorder Traversal Examples

Inorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Algorithm To Find Preorder Traversal:

  1. If root is NULL, return NULL.
  2. Print the node.
  3. Visit left subtree.
  4. Visit right subtree.

Code Implementation for Preorder Tree traversal

Run 
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};
void preorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Print the data
  cout << root->data << " ";
  // Visit Left subtree
  preorder_traversal (root->left);
  // Visit right subtree
  preorder_traversal (root->right);
}

int main ()
{
  Tree *root = new Tree (15);
  root->left = new Tree (12);
  root->right = new Tree (54);
  root->left->left = new Tree (8);
  root->left->right = new Tree (13);
  root->left->left->left = new Tree (5);
  root->right->left = new Tree (18);
  preorder_traversal (root);
  return 0;
}


Output:

15 12 8 5 13 54 18

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java