Binary Search Tree Program

March 19, 2025

Binary Search Tree Program

A binary search tree is a tree in which the data in left subtree is less than the root and the data in right subtree is greater than the root. In this article , we will cover all the basics of binary search tree.

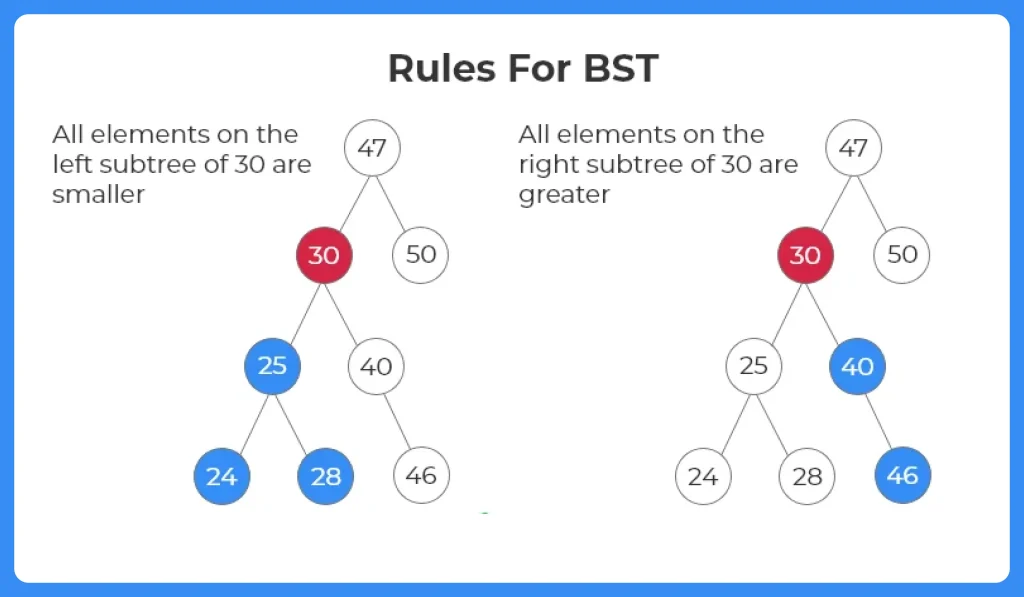
Binary Search Tree
Binary Search Tree

Reprsentation Of BST:

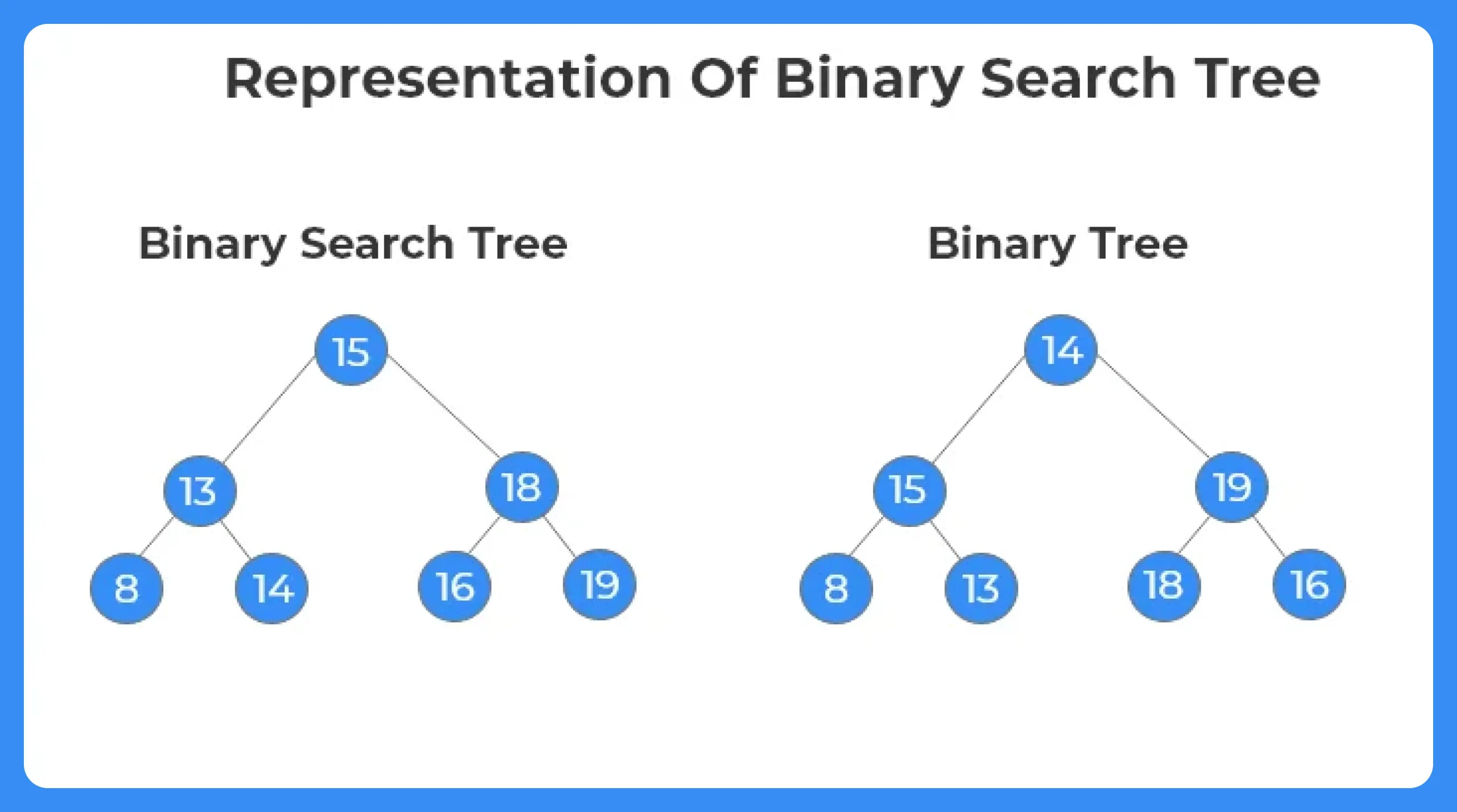
  1. The representation of a BST is similar to that of a binary tree. The order of a BST is ‘2’. Each node can have at most two children.
  2. Only difference between the two is that there is a certain criteria of arrangement or insertion of the elements based on their comparisons with the root node and the sub tree segment they are added to.
Binary Search Tree 1

Operations In A BST:

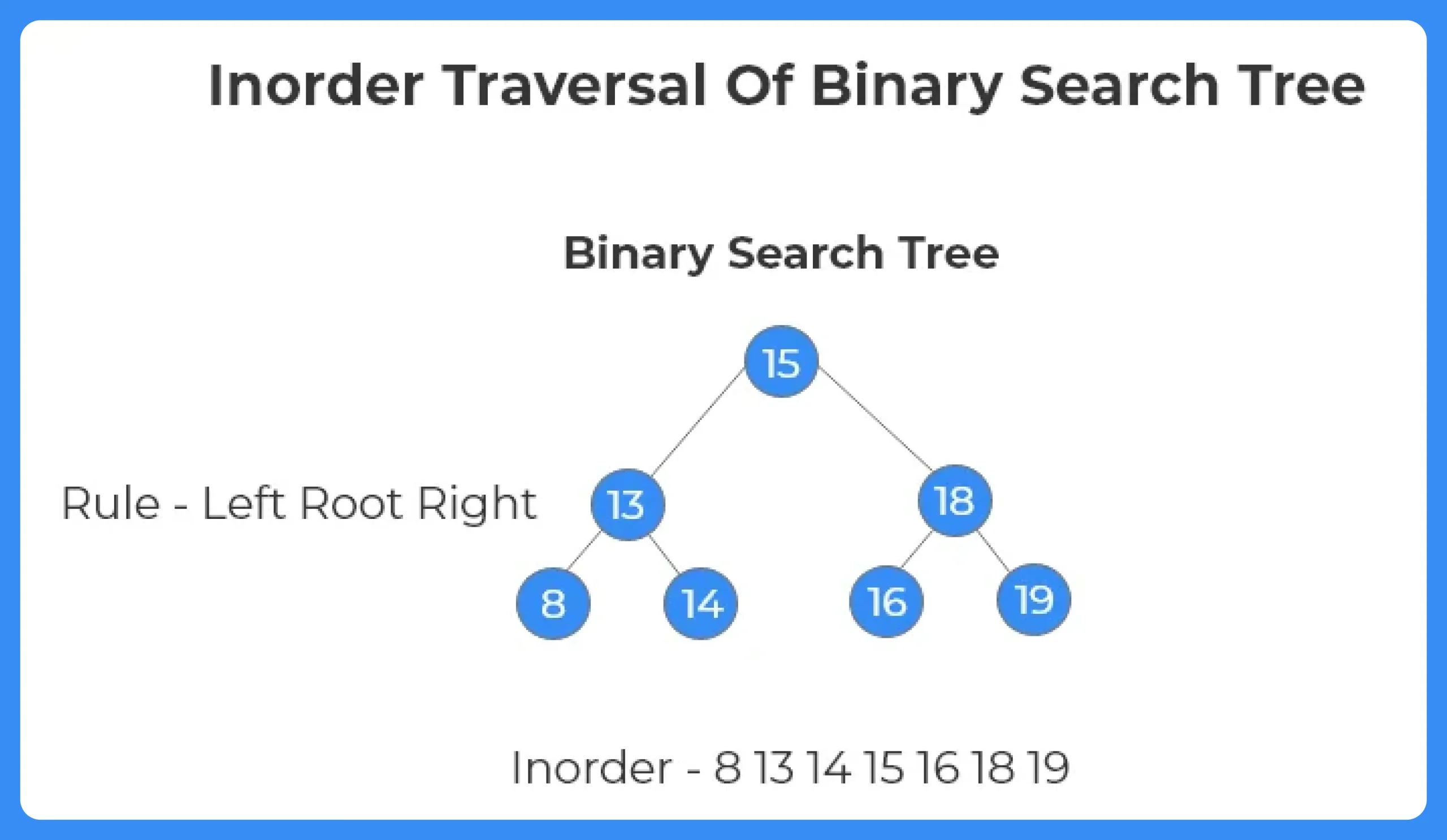
  1. Traversal
  2. Searching
  3. Insertion
  4. Deletion

Features Of A BST:

  1. Fast look-up.
  2. Efficient addition and removal of items.
  3. Used to implement dynamic set of items

Tree Traversals: Inorder Postorder Preorder

Inorder Tree Traversal in Binary Tree

Inorder Tree Traversal without Recursion

Preorder Tree Traversal without Recursion

BST: Search a node in Binary Search Tree

Binary Search Tree 2

Code For Binary Search Tree​

Run 
#include<stdio.h>
#include<stdlib.h>

struct node
{
  int data;
  struct node *left;
  struct node *right;
};

struct node *create_node (int data)
{
  struct node *new_node = (struct node *) malloc (sizeof (struct node));
  new_node->data = data;
  new_node->left = NULL;
  new_node->right = NULL;
  return new_node;
}

struct node *insert_node (struct node *root, int data)
{
  if (root == NULL)
    {
      return create_node (data);
    }
  if (data < root->data)
    {
      root->left = insert_node (root->left, data);
    }
  else
    {
      root->right = insert_node (root->right, data);
    }
  return root;
}

struct node *search_node (struct node *root, int data)
{
  if (root == NULL || root->data == data)
    {
      return root;
    }
  if (data < root->data)
    {
      return search_node (root->left, data);
    }
  else
    {
      return search_node (root->right, data);
    }
}

void inorder (struct node *root)
{
  if (root != NULL)
    {
      inorder_traversal (root->left);
      printf ("%d ", root->data);
      inorder_traversal (root->right);
    }
}

int main ()
{
  struct node *root = NULL;
  root = insert_node (root, 50);
  insert_node (root, 30);
  insert_node (root, 20);
  insert_node (root, 40);
  insert_node (root, 70);
  insert_node (root, 60);
  insert_node (root, 80);
  inorder (root);
  return 0;
}

Output :

20 30 40 50 60 70 80

Advantages Of BST:

  1. Inorder Traversal gives sorted order of elements.
  2. Easy to implement order statistics.
  3. Helpful in range queries.

Disadvantages Of BST:

  1. The cost of operations may be high.
  2. Shape of tree depends on insetions and may be degenerated.