Searching in Binary Tree

March 23, 2023

Searching In A Binary Tree

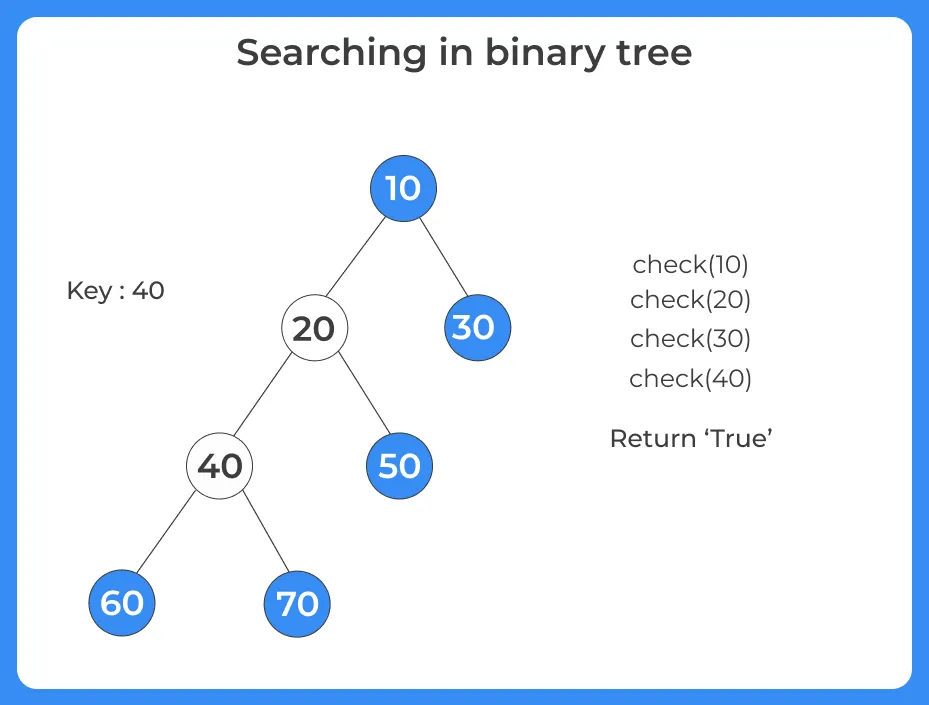
Given a tree and the number, we need to find to check whether the number is present in the binary tree or not. There can be different ways to approach this problem. In this articles, two ways are discussed, level order and recursion.

searching in binary tree

Binary Tree

  • A Binary Tree is a data structure with maximum of two children for each parent.
  • Level Order Traversal is an example Of Breadth First Search algorithm.
  • Level order is a traversal in which each node is visited in the level before we move to a lower level.
  • Queues are used to find the level order traversal.
Searching in binary tree
DSA desktop gif
DSA mobile gif

Searching in a Binary Search Tree

AVL Tree Insertion

Depth First Traversals

Level Order Traversal

Construct Tree from given Inorder and Preorder traversals

Algorithm

  • Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
  • When a node is created, data will pass to data attribute of the node and both left and right will be set to null.
  • Define another class which has two attribute root and flag.
    1. Root represents the root node of the tree and initializes it to null.
    2. The Flag will be used to check whether the given node is present in the tree or not. Initially, it will be set to false.
  • searchNode() will search for a particular node in the binary tree:
    1. It checks whether the root is null, which means the tree is empty.
    2. If the tree is not empty, it will compare temp?s data with value. If they are equal, it will set the flag to true and return.
    3. Traverse left subtree by calling searchNode() recursively and check whether the value is present in left subtree.
    4. Traverse right subtree by calling searchNode() recursively and check whether the value is present in the right subtree.
Run 
class Node
{
  int key;
  Node left, right;
  public Node (int item)
  {
    key = item;
    left = right = null;
  }
}

class BinaryTree
{
// Root of Binary Tree
  Node root;

    BinaryTree ()
  {
    root = null;
  }

  

/* Given a binary tree, print its nodes in inorder*/
  void inorder (Node ptr)
  {
    if (ptr == null)
      return;

/* first recur on left child */
    inorder (ptr.left);

/* then print the data of node */
    System.out.print (ptr.key + " ");

/* now recur on right child */
    inorder (ptr.right);
  }

 
   boolean ifNodeExists(Node node,int key)
{
    if (node == null)
        return false;
 
    if (node.key == key)
        return true;
 
    // then recur on left subtree /
    boolean res1 = ifNodeExists(node.left, key);
   
    // node found, no need to look further
    if(res1) return true;
 
    // node is not found in left,
    // so recur on right subtree /
    boolean res2 = ifNodeExists(node.right,key);
 
    return res2;
}
  
}

public class Main
{
  public static void main (String[]args)
  {
    BinaryTree tree = new BinaryTree ();
      tree.root = new Node (1);
      tree.root.left = new Node (2);
      tree.root.right = new Node (3);
      tree.root.left.left = new Node (4);
      tree.root.left.right = new Node (5);

      System.out.println ("\nInorder traversal");
      tree.inorder (tree.root);
      System.out.println("");
     
      System.out.println("\n3 is present in the tree:  "+tree.ifNodeExists(tree.root,3));
      System.out.println("\n8 is present in the tree:  "+tree.ifNodeExists(tree.root,8));
  }
}

Output:

Inorder traversal
4 2 5 1 3 
3 is present in the tree:  true
8 is present in the tree:  false

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java