Inorder Tree Traversal in Binary Tree In C++

August 8, 2025

Inorder Tree Traversal

Inorder Traversal in Binary Tree in C++ – Inorder traversal is a common method to visit all nodes in a binary tree. It follows the Left → Root → Right order. This means we first visit the left subtree, then the root node, and finally the right subtree. In a Binary Search Tree (BST), this gives us the values in sorted order.

In this blog, we’ll see how to implement Inorder Traversal in C++ with easy examples and clear explanations. Inorder traversal is a depth first algorithm. There are three types of traversals in tree: Preorder, Inorder, Postorder. In this article, inorder tree traversal is performed using recursion.

Inorder Tree Traversal In Binary Tree in C++ language

Inorder Tree Traversal in Binary Tree in C++

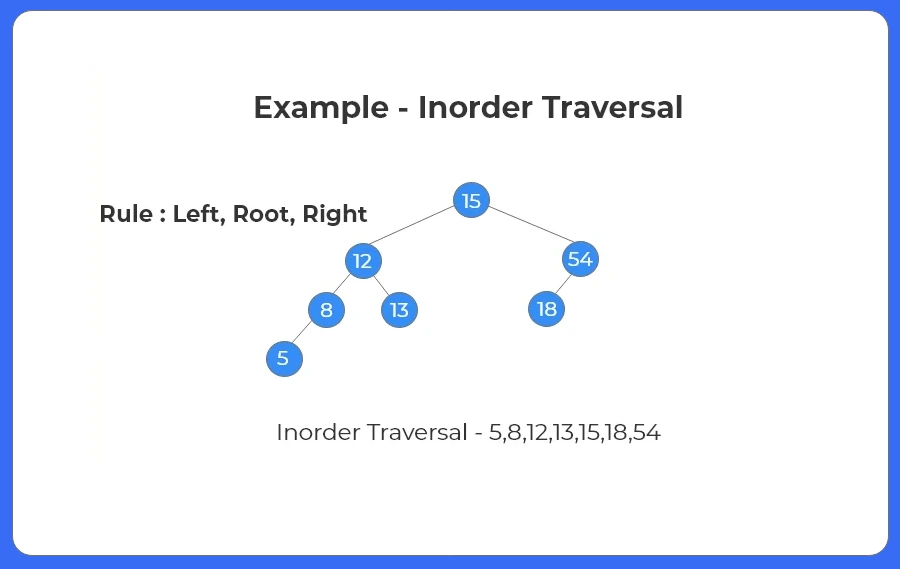
Inorder traversal is a type of depth-first traversal where the nodes are visited in the following order:
first the left subtree, then the root node, and finally the right subtree.

Steps To Find Inorder Traversal:

  1.  Leftmost node is 5 so print 5
  2.  Move back, print 8 and look for right child.
  3.  As there is no right child, print 12 and move to the right subtree.
  4. 13 is printed and whole subtree is covered.
  5. Print 15 and move to the right subtree.
  6. 18 and 54 are printed and tree is covered.
Inorder Tree traversal in binary tree in cpp

What is Inorder generally used for?

We generally use Inorder traversal technique on Binary Tress , as it fetches the values from the underlying set in order. Using Post-order traversal is also an option, but during post order traversal while delete or freeing nodes it can even delete or free an entire binary tree, which is not a favorable condition.

DSA desktop gif
DSA mobile gif

Trees in Data Structure(Introduction)

Types of Trees in data structure

Inorder Postorder Preorder Traversal Examples

Preorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Algorithm To Find Inorder Traversal:

  1. If root is NULL, return NULL.
  2. Visit the left subtree.
  3. Print the node.
  4. Visit the right subtree.

Code Implementation for Inorder Tree traversal

Run 
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};
void inorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Visit Left subtree
  inorder_traversal (root->left);
  // Print the data
  cout << root->data << " ";
  // Print the right subtree
  inorder_traversal (root->right);
}

int main ()
{
  Tree *root = new Tree (15);
  root->left = new Tree (12);
  root->right = new Tree (54);
  root->left->left = new Tree (8);
  root->left->right = new Tree (13);
  root->left->left->left = new Tree (5);
  root->right->left = new Tree (18);
  inorder_traversal (root);
  return 0;
}


Output:
5 8 12 13 15 18 54

Conclusion

Inorder traversal is one of the most important and commonly used methods to go through a binary tree, especially when dealing with Binary Search Trees. It helps in visiting nodes in a sorted manner, first the left child, then the root, and finally the right child. Whether you use recursion or iteration, understanding how Inorder traversal works builds a strong foundation for solving many tree-related problems in C++.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

FAQs - Inorder Tree Traversal in Binary Tree In C++

FAQs - Inorder Tree Traversal in Binary Tree In C++

Inorder traversal alone cannot uniquely reconstruct a binary tree because it does not provide enough information about the tree structure. However, if combined with either preorder or postorder traversal, the original binary tree can be reconstructed.

  • Recursive Inorder Traversal has a time complexity of O(n) and space complexity of O(h), where h is the height of the tree (due to call stack usage).
  • Iterative Inorder Traversal using a stack also takes O(n) time and O(h) space for the stack.

In a valid BST, the Inorder traversal should produce values in strictly increasing order. If the sequence is not sorted or has duplicates (when not allowed), the tree is not a valid BST.

Morris Inorder Traversal is an advanced method that performs traversal without using a stack or recursion. It uses a concept called threaded binary trees and modifies tree links temporarily to achieve O(1) space complexity. However, it’s more complex and not typically used in basic scenarios.

Inorder traversal is best suited for Binary Search Trees where sorted output is useful. However, in general binary trees, it may not provide meaningful node processing order depending on the problem. For tasks like serialization or hierarchy-based processing, preorder or level-order might be more appropriate.

This is possible through Morris Traversal, which temporarily modifies the tree structure by creating links to predecessors and restores it after traversal. It’s tricky to implement but avoids extra memory usage, making it space-efficient.

Stacks

  • Introduction to Stack in Data Structure
    Click Here
  • Operations on a Stack
    Click Here
  • Stack: Infix, Prefix and Postfix conversions
    Click Here
  • Stack Representation in –
    C | C++ | Java
  • Representation of a Stack as an Array. –
    C | C++ | Java
  • Representation of a Stack as a Linked List. –
    C | C++ | Java
  • Infix to Postfix Conversion –
    C | C++ | Java
  • Infix to prefix conversion in –
    C | C++ | Java
  • Postfix to Prefix Conversion in –
    C | C++ | Java

Queues

  • Queues in Data Structures (Introduction)
    Click Here
  • Queues Program in C and implementation
    Click Here
  • Implementation of Queues using Arrays | C Program
    Click Here
  • Types of Queues in Data Structure
    Click Here
  • Application of Queue Data Structure
    Click Here
  • Insertion in Queues Program (Enqueuing) –
    C | C++ | Java
  • Deletion (Removal) in Queues Program(Dequeuing) –
    C | C++ | Java
  • Reverse a Queue –
    C | C++ | Java
  • Queues using Linked Lists –
    C | C++ | Java
  • Implement Queue using Stack –
    C | C++ | Java
  • Implement Queue using two Stacks –
    C | C++ | Java

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction –
    C | C++ | Java
  • Priority Queue Implementation using Array –
    C | C++ | Java
  • Priority Queue using Linked List –
    C | C++ | Java
  • Priority Queue Insertion and Deletion-
    C | C++ | Java

Stacks

Queues

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction – C | C++ | Java
  • Priority Queue Implementation using Array – C | C++ | Java
  • Priority Queue using Linked List – C | C++ | Java
  • Priority Queue Insertion and Deletion- C | C++ | Java

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout