Postfix to Prefix Conversion Program using Stack in C++

November 13, 2025

Postfix to Prefix Conversion in C++

Postfix to Prefix Conversion in C++ – Prefix, Postfix and Infix are the different ways to write expressions as notations. In infix, they are normal notations as used by mathematical expressions in copies. In Prefix expression, the  operator is prefixed to operands, and in Postfix, or Reverse Polish Notation, the operator comes after the operands. In this article we will know how to perform Post fix expressions to prefix expressions converstion using a stack in C++.

Postfix to prefix expression

What is Postfix to Prefix Conversion in C++?

Infix: (X + Y)

  • Postfix – The postfix will look like, XY+
  • Prefix: The prefix will look like, +YX

Infix : (X + Y) / (U – V)

  • Postfix – The postfix will look like, XY+UV-/
  • Prefix – The prefix will look like, /+XY-UV

Here we need to use a stack data structure. SInce we have our own inbuilt stack DS in C++ STL, we are going to use it. If you use want to know more about that : Stack in C++ STL 

Follow this algorithm to solve this problem

There may be  many ways to find the post fix to prefix, here it goes one easy way to imlement an algorithm to do so.

  • Read the expression from left to right.
  • If there is any operand present, push it to a stack.
  • Then if you come accross an operator, pop two of the opearands from the stack and concatinate them like,
    the operator + 2nd top value of the stack + first top value of the stack.
  • Repeat the process.
  • Reverse the string at the end.

Fun fact: This can be interpreted as a binary tree if you can make a binary tree with operators and add the operands at last.

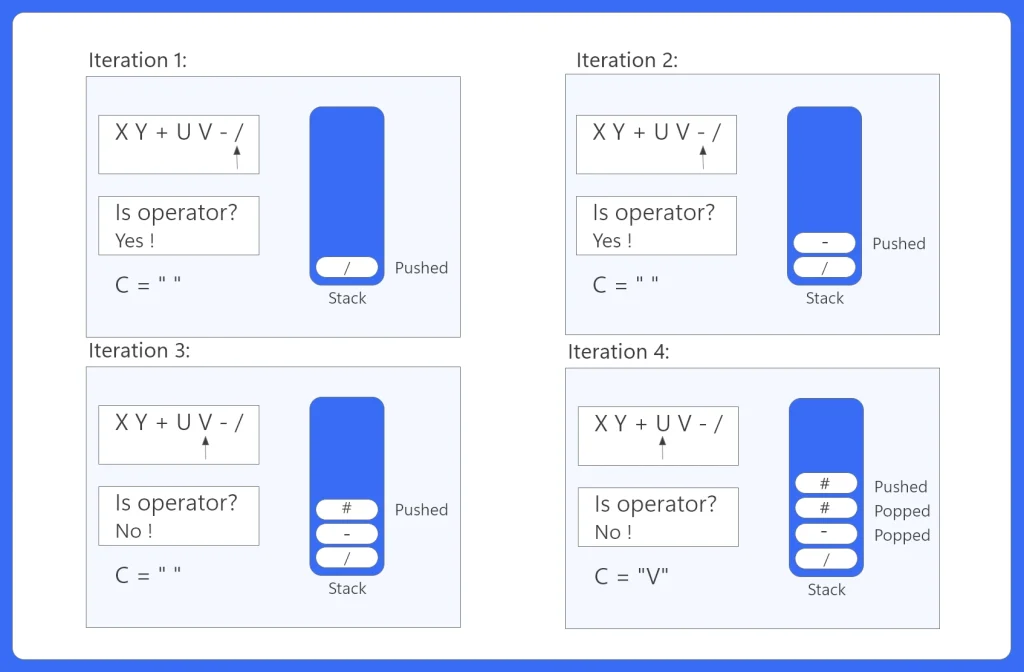
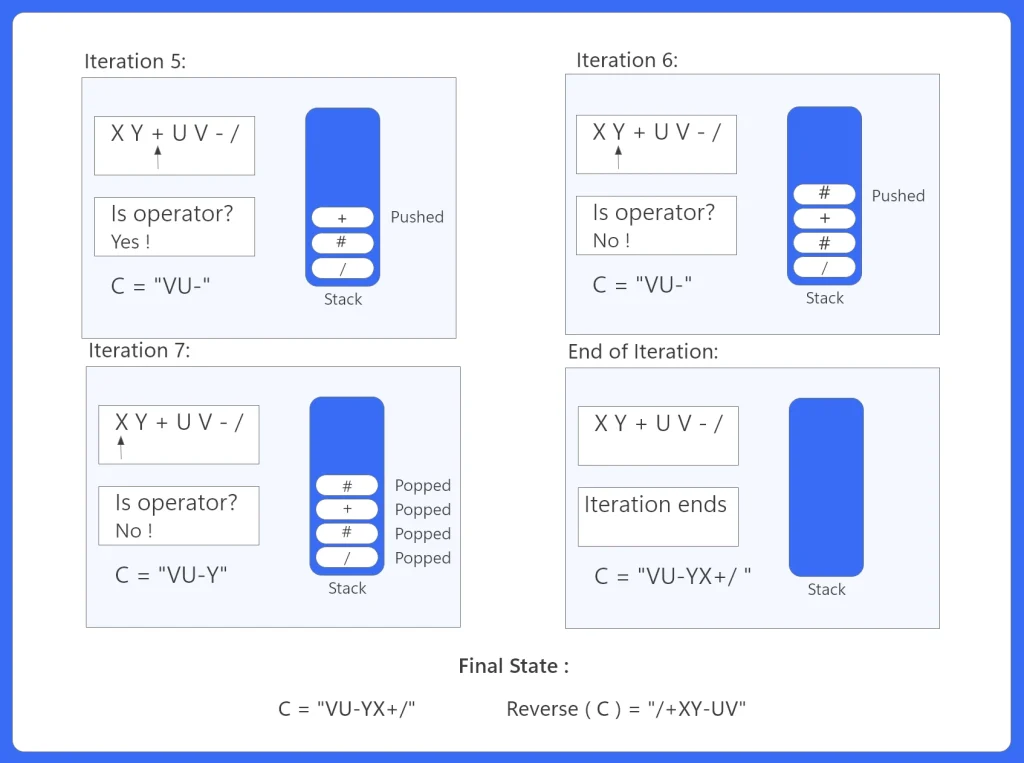
Visual Implementation of the Algorithm :

Suppose the expression in Infix is (X+Y)/(U-V), and in Postfix: XY+UV-/ 

Here all the iterations are shown below.

Postfix to prefix conversion-2
Postfix to prefix conversion – 1

Stack Representation in C++

Representation of a Stack as an Array

Representation of a Stack as a Linked List

Infix to postfix conversion

Infix to prefix expression

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

The code to implement this:

This C++ implementation uses a stack to transform postfix expressions into prefix form with clean logic and minimal complexity. By handling operators and operands systematically, the program delivers accurate results in just a few steps. It’s a simple yet powerful technique for expression manipulation.

Run

#include <bits/stdc++.h>
using namespace std;

bool isOperator(char x) {
    return (x == '+' || x == '-' || x == '*' || x == '/');
}

string postToPre(string post_exp) {
    stack s;

    for (int i = 0; i < post_exp.length(); i++) {
        char ch = post_exp[i];

        if (isOperator(ch)) {
            string op2 = s.top(); s.pop();
            string op1 = s.top(); s.pop();
            string temp = ch + op1 + op2;
            s.push(temp);
        } else {
            s.push(string(1, ch));
        }
    }

    return s.top();
}

int main() {
    string postfix;
    cout << "Enter the Postfix Expression: "; cin >> postfix;

    string prefix = postToPre(postfix);
    cout << "The Prefix expression is: " << prefix << endl;

    return 0;
}

Input :

ABC*+

Output:

+ A * B C

Explanation:

  • The program converts a postfix expression into a prefix expression using a stack-based approach for operator and operand manipulation.
  • Each character from the postfix expression is processed  operands are directly pushed onto the stack, while operators trigger the popping and combination of two operands.
  • When an operator is encountered, two top elements are popped from the stack, combined with the operator in prefix order, and then pushed back.
  • At the end of traversal, the stack contains one element, which is the required prefix expression.
  • The approach efficiently handles conversion by maintaining proper order and precedence through stack operations.

Time and Space Complexity:

OperationComplexityExplanation
Time ComplexityO(n²)String concatenation causes repeated copying of growing strings.
Space ComplexityO(n)Stack stores intermediate expressions; final string is size n.

To wrap it up:

This article has provided a clear walkthrough of how to convert a postfix expression into prefix form using a stack in C++, detailing the algorithm, example transformations, and a practical code implementation. By using a stack of strings and repeatedly combining operands with operators, this method respects operator precedence and handles nested expressions effectively.

Equipped with the algorithm, code sample, and key FAQs, you’re now prepared to implement this conversion in your own C++ programs and understand how each step ensures correct evaluation without relying on parentheses.

FAQs - Postfix to Prefix Conversion in C++

FAQs - Postfix to Prefix Conversion in C++

In Postfix to Prefix conversion, each subexpression (like +AB) can be more than one character. Using a stack<string> allows handling full subexpressions and prevents incorrect concatenation or type errors.

Prefix notation inherently preserves operator precedence by placing the operator before its operands. The conversion process constructs expressions recursively using the stack, thus eliminating the need for explicit parentheses.

Edge cases include: insufficient operands, extra operators, invalid characters, or single-character input. These should be validated before processing, and the stack should always contain exactly one element at the end for a valid expression.

The algorithm naturally handles nested sub-expressions by using a stack: when an operator is encountered, the top two operands (which can be full sub-expressions) are popped, combined, and pushed back—thus preserving correct nesting order.

Postfix expressions are evaluated from left to right because operands appear before the operator. This order ensures the top two elements on the stack are always the correct operands for the current operator being processed.

Both time and space complexity are O(n), where n is the length of the postfix expression. The size of intermediate expressions and the number of operators affect the space required by the stack during execution.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Stacks

  • Introduction to Stack in Data Structure
    Click Here
  • Operations on a Stack
    Click Here
  • Stack: Infix, Prefix and Postfix conversions
    Click Here
  • Stack Representation in –
    C | C++ | Java
  • Representation of a Stack as an Array. –
    C | C++ | Java
  • Representation of a Stack as a Linked List. –
    C | C++ | Java
  • Infix to Postfix Conversion –
    C | C++ | Java
  • Infix to prefix conversion in –
    C | C++ | Java
  • Postfix to Prefix Conversion in –
    C | C++ | Java

Queues

  • Queues in Data Structures (Introduction)
    Click Here
  • Queues Program in C and implementation
    Click Here
  • Implementation of Queues using Arrays | C Program
    Click Here
  • Types of Queues in Data Structure
    Click Here
  • Application of Queue Data Structure
    Click Here
  • Insertion in Queues Program (Enqueuing) –
    C | C++ | Java
  • Deletion (Removal) in Queues Program(Dequeuing) –
    C | C++ | Java
  • Reverse a Queue –
    C | C++ | Java
  • Queues using Linked Lists –
    C | C++ | Java
  • Implement Queue using Stack –
    C | C++ | Java
  • Implement Queue using two Stacks –
    C | C++ | Java

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction –
    C | C++ | Java
  • Priority Queue Implementation using Array –
    C | C++ | Java
  • Priority Queue using Linked List –
    C | C++ | Java
  • Priority Queue Insertion and Deletion-
    C | C++ | Java

Stacks

Queues

Circular Queues

Priority Queue

  • Application of Priority Queue
  • Priority Queue Example
  • Priority Queue Introduction – C | C++ | Java
  • Priority Queue Implementation using Array – C | C++ | Java
  • Priority Queue using Linked List – C | C++ | Java
  • Priority Queue Insertion and Deletion- C | C++ | Java