Operations on a Stack

June 28, 2022

Operations on a Stack

There are many operations that can be used to manipulate a stack. A stack is a data structure in which the operations are executed in constant time.

There are a number of operations that can be performed on a stack, but there are two major operations that are used to manipulate a stack.

These operations are:

  • Push()
  • Pop()

Push()

  • The push operation in a stack is synonymous to insertion in a data structure.
  • In simpler words, inserting a new  element in a stack is known as push.
  • The time complexity of the Push() operation is O(1), i.e , it occurs in constant time.

Let us understand how a push() operation works. Let us consider we have to push a given number of elements in the stack.

The elements to be inserted are: 12 , 08 , 21 , 33 , 18 , 40.

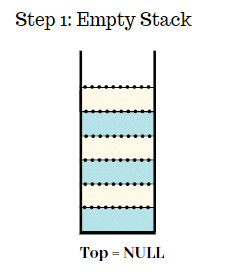
Step 1:

  • Initially we have an empty stack.
  • Top = NULL.

Step 2:

  • Push the element 12 in the stack.
  • Top = 12

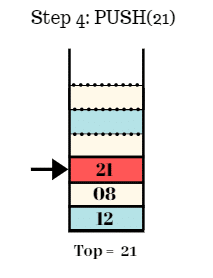
Step 3:

  • Push the element 08 in the stack.
  • Top = 08.

Step 4:

  • Push the element 21 in the stack.
  • Top = 21

Step 5:

  • Push the element 33 in the stack.
  • Top = 33.

Step 6:

  • Push the element 18 in the stack.
  • Top = 18

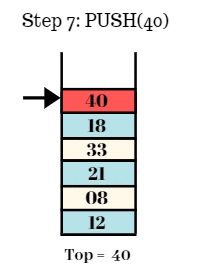
Step 7:

  • Push the element 40 in the stack.
  • Top = 40.

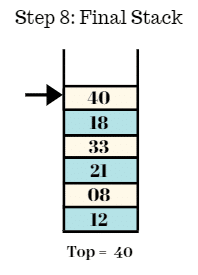
Step 8:

  • Final stack is shown as follows.
  • Top = 40

Pop()

  • The Pop operation in a stack is synonymous to deletion in a data structure.
  • In simpler words, deleting an existing element from a stack is known as pop.
  • The time complexity of the Pop() operation is O(1), i.e , it occurs in constant time.

Let us understand how a pop() operation works. Let us consider we have to pop a given number of elements in the stack.

The elements to be deleted from the stack are : 40 , 18 , 33. 

Step 1:

  • The first element to be deleted from the stack is 40.
  • We can see the value of top points to 40.
  • We perform the pop operation and the element 40 is popped out off the stack.
  • The remaining elements are shown in the image.
  • Top = 18.

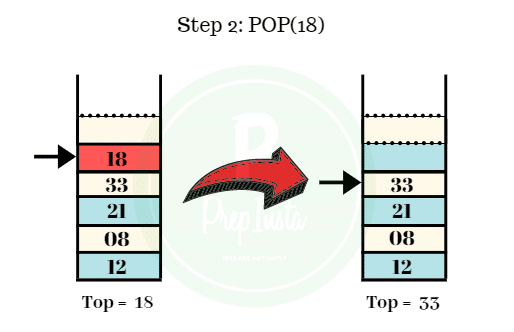
Step 2:

  • The second element to be deleted from the stack is 18.
  • We can see the value of top points to 18.
  • We perform the pop operation and the element 18 is popped out off the stack.
  • The remaining elements are shown in the image.
  • Top = 33.

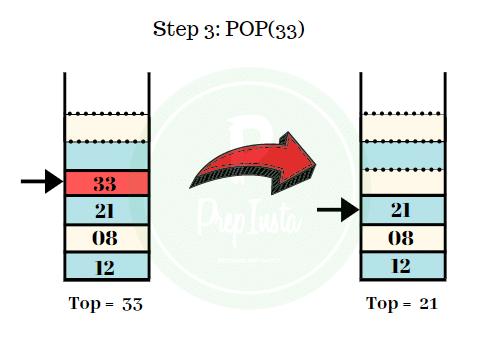
Step 3:

  • The next element to be deleted from the stack is 33.
  • We can see the value of top points to 33.
  • We perform the pop operation and the element 33 is popped out off the stack.
  • The remaining elements are shown in the image.
  • Top = 21.

Code for Stack in C Program (using structure)

Run 
// C Program for Implmentation of stack (array) using structure
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
  
// A structure to represent a stack 
struct Stack { 
    int top; 
    int maxSize; 
    int* array; 
}; 

struct Stack* create(int max) 
{ 
    struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack)); 
    stack->maxSize = max; 
    stack->top = -1; 
    stack->array = (int*)malloc(stack->maxSize * sizeof(int));
    //here above memory for array is being created
    // size would be 10*4 = 40
    return stack; 
} 

// Checking with this function is stack is full or not
// Will return true is stack is full else false 
//Stack is full when top is equal to the last index 
int isFull(struct Stack* stack) 
{ 
    if(stack->top == stack->maxSize - 1){
        printf("Will not be able to push maxSize reached\n");
    }
    // Since array starts from 0, and maxSize starts from 1
    return stack->top == stack->maxSize - 1; 
} 
  
// By definition the Stack is empty when top is equal to -1 
// Will return true if top is -1
int isEmpty(struct Stack* stack) 
{ 
    return stack->top == -1; 
}

// Push function here, inserts value in stack and increments stack top by 1
void push(struct Stack* stack, int item) 
{ 
    if (isFull(stack)) 
        return; 
    stack->array[++stack->top] = item; 
    printf("We have pushed %d to stack\n", item); 
}

// Function to remove an item from stack.  It decreases top by 1 
int pop(struct Stack* stack) 
{ 
    if (isEmpty(stack)) 
        return INT_MIN; 
    return stack->array[stack->top--]; 
} 
  
// Function to return the top from stack without removing it 
int peek(struct Stack* stack) 
{ 
    if (isEmpty(stack)) 
        return INT_MIN; 
    return stack->array[stack->top]; 
} 

int main()
{
struct Stack* stack = create(10); 
  
    push(stack, 5); 
    push(stack, 10); 
    push(stack, 15);
    
    int flag=1;
    while(flag)
    {
        if(!isEmpty(stack))
            printf("We have popped %d from stack\n", pop(stack));
        else
            printf("Can't Pop stack must be empty\n");
         flag=0;
    }
    return 0;
}

Output :

We have pushed 5 to stack                         
We have pushed 10 to stack
We have pushed 15 to stack
We have popped 15 from the stack
Do you want to Pop again? Yes: 1 No: 0
0