Binary Trees in Data Structures (Introduction)

May 1, 2020

Introduction

A binary tree can be defined as a finite set of elements, which can either be empty or have at most two children.
A binary tree can either be empty or be divided into three disjoint subsets.
The first subset constitutes of a single element called the root.
The other two subsets are namely, left child and a right child. These subsets can be empty.
Each entity that holds a value or data is termed as a node.

Properties of a Binary tree

The order of a binary tree is ‘2’.
In a binary tree, each node can have at most 2 children.
A binary tree can be empty.
A binary tree does not permit duplicate value.
Height of a binary tree is equal to the height of the root node.
Height of a particular node, under consideration, is the number of edges extending from that node to the deepest leaf.
Depth of a particular node, under consideration, is the number of edges extending from the root node till that node.

Operations Performed

Traversal .
Insertion
Deletion.

Types of Binary tree

1. Full Binary Tree

A binary tree is said to be a Full binary tree if all nodes except the leaf nodes have either 0 or 2 children. In other words the degree of such tree can either be 0 or 2.
In the given image, we can see that,
- nodes ‘a’, ‘b’, ‘e’ have two child nodes each.
- nodes ‘c’, ‘d’ have 0 child nodes.
Hence the given example is a full binary tree, also called strict binary tree.

2. Complete Binary Tree

A binary tree is said to be a Complete binary tree if all the levels are completely filled except possibly the last level; and the last level has all the keys towards left.
In the given image, we can see that all the levels are fully filled with two child nodes each except the last levels which are oriented towards as left as possible, i.e,
- the nodes ‘a’, ‘b’, ‘c’, ‘d’ have two child nodes each.
- and the leaf nodes ‘h’, ‘i’, ‘j’ are oriented towards the left.
Hence, the given example can be concluded as a complete binary tree.

3. Perfect Binary Tree

A binary tree is said to be a Perfect binary tree if all the internal nodes have exactly 2 children.
In the given image, we can see that each node in the tree except the leaf nodes have exactly two children, i.e, the nodes ‘a’, ‘b’, ‘c’ have exactly two children each.

4. Balanced Binary Tree

A binary tree is said to be a Balanced binary tree if, for each node it holds that the number of inner nodes in the left sub tree and the number of inner nodes in the right sub tree differ by at most 1.
In this image, we can see at different respective levels the difference in height between the left and the right sub trees. For instance,
- at node ‘a’ the difference between the left sub tree ‘b’ and the right sub tree ‘c’ is 1.
- at node ‘e’ the difference between the left sub tree ‘—‘ and the right sub tree ‘j’ is 1.
- at node ‘d’ the difference between the left sub tree ‘h’ and the right sub tree ‘i’ is 0.
From this we can conclude that the given image is an example of a balanced binary tree.

Representation of a Binary tree in Memory

In a binary tree, each node consists of a data field and since binary tree is of recursive nature, it also contains a pointer.

Hence the representation of a binary tree can be extended to two ways :

Sequential representation(Arrays).
Dynamic node representation(Linked lists).

A structure that defines a node of a binary tree is shown as follows:

struct tree_node

{
    struct tree_node *left;
    int data;
    struct tree_node *right;
}

Yeah ! Let us write a sample program to create our first basic tree

#include<stdio.h>
#include<stdlib.h>

//PrepInsta, creating basic node structure : data, left/right node pointers
struct node  
{ 
    int data; 
    struct node* left; 
    struct node* right; 
}; 
  
/* This function is creating memory for new node struct
   and allocating values to data and left-right pointers */
struct node* newNode(int data) 
{ 
  // Using malloc to create memory for new node to be created
  struct node* node = (struct node*)malloc(sizeof(struct node)); 
  
  // Assigning data
  node->data = data; 
  
  // Here we assign left-right children nodes to NULL
  node->left = NULL; 
  node->right = NULL; 
  
  //finally returning node
  return(node); 
} 
  
  
int main() 
{ 
  /*Root is created first*/
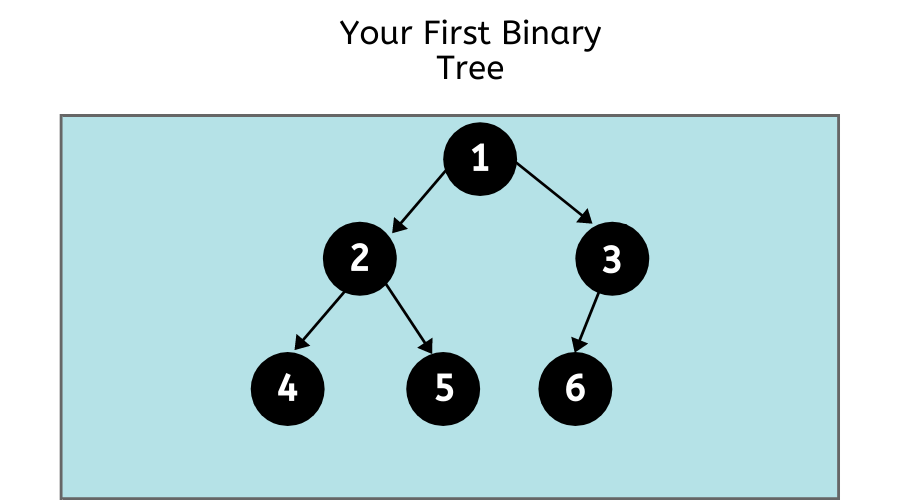
  struct node* root = newNode(1);   
  /* This is how the tree looks now.....
  
        1 
      /   \ 
     NULL  NULL   
  */
    
  
  root->left        = newNode(2); 
  root->right       = newNode(3); 
  /* 2 and are now left and right children to root node
           1 
         /   \ 
        2       3 
     /    \    /  \ 
    NULL NULL NULL NULL 
  */
  
  
  root->left->left  = newNode(4); 
  root->left->right  = newNode(5); 
  root->right->left  = newNode(6); 
  /* 4 and 5 becomes children of 2 
            1 
        /       \ 
       2          3 
     /   \       /  \ 
    4    5      6  NULL 
  /  \  / \    / \
NULL N N   N  N   N
*/

printf("The tree has been created");
printf("\nWe will understand printing later");
printf("\nWhen we learn, traversals (inorder, postorder, preorder etc");
  
  return 0; 
}

Other methods to Create Tree

1. Sequential Representation(using Array)

Let us consider a complete binary tree BT which is represented using an array T keeping in mind the following points:

- The root node N of the tree BT is placed on index T[1] and all other nodes of the tree are placed recursively.
- If a node is placed on T[k],
  1. The left child of the node is found on the position T[2*k].
  2. The right child of the node is found on the position T[(2*k) + 1].
  3. The parent node of the node is found on the position T[k/2].

Taking the example above as reference, we can see:

All the elements are indexed as per their position. The null nodes extending from leaves have also been indexed.
Corresponding to it if we see the array, the index of the null nodes hold the value ‘\0’.
Rest of the elements are placed on their respective indices. Also observe that here the indexing begins from 1.

2. Dynamic node Representation(using linked list)

Binary trees can be represented using linked lists. Each node contains the address of the left and the right child. The leaf nodes contain a NULL value in its link field since it doesn’t have a left or a right child.

Let us consider a binary tree BT consisting of a node N corresponding to a location k which is represented as linked list L keeping in mind the following points:

1. Left[k] points to the location of the left child of the node.
2. Right[k] points to the location of the right child of the node.
3. Data[k] consists of the data of the node.

Taking the example above as reference, the linked list representation of the tree is shown as follows:

Applications of a Binary Tree

Binary trees are data structures that are used to represent hierarchies.
They are flexible and powerful data structures.
They provide efficient insertion and deletion operations.