Insertion in AVL Tree In C++
Insertion In AVL Tree
AVL tree is self balancing tree in which for all nodes, the difference of height between the left subtree and the right subtree is less than or equal to 1. In this article, an avl tree is created and the difference of height is printed for each node.

Insertion and Creation of an AVL Tree
- A new node can be inserted in an AVL tree by determining the correct position of the node. But insertion of a new node into the tree may affect the height of the tree and the tree might become unbalanced.
- If the new nodes are inserted as child nodes on a non- leaf node there will be no alteration since there will be no effect on the balancing as there is no increase in the height of the tree.
- If the new nodes are inserted as child nodes on a leaf node, the balancing of the tree might get distorted. This depends on whether the node is added to the left subtree or the right subtree.
- Thus to re-balance the tree in order to conserve it’s characteristics we use Rotation Mechanism. There are four types of rotations which help maintain the balancing of the tree as specified above.
- If, due to insertion,the b_fact of multiple nodes is disturbed, balancing occurs on the first ancestor of the node that has been inserted.
Note: During the process of insertion it is important to check the balancing factor of each node at each step, until the process end.
Let us understand with the help of an example. Consider we have following elements given to us: [ 15 , 18 , 12 , 8 , 54 , 5 , 14 , 13 , 9 , 60].
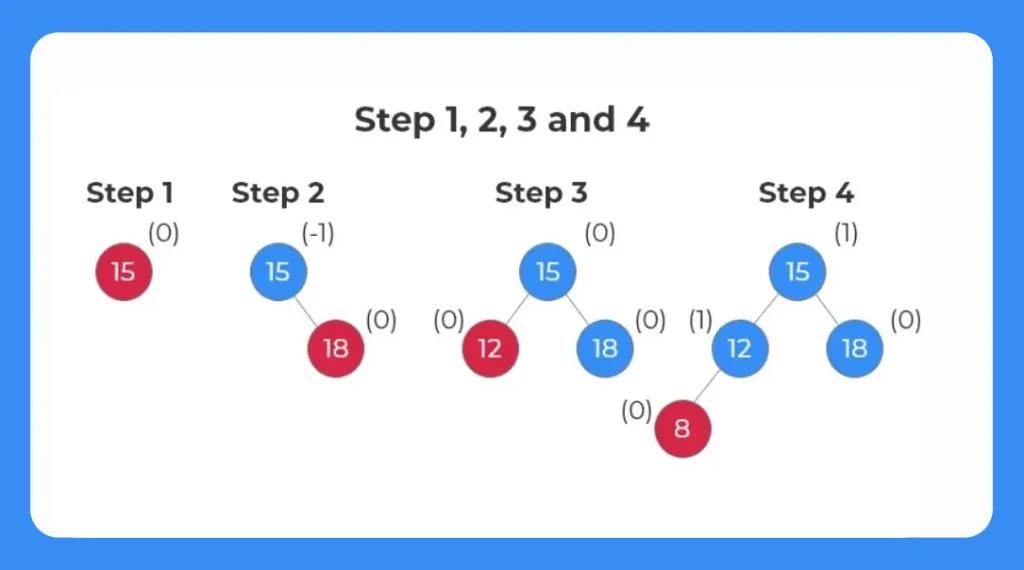
Step 1:
- Insert the first element 15.
- Check for the b_fact of the node.
- b_fact= 0
Step 2:
- Insert the next element 18.
- Check the b_fact each node.
Step 3:
- Insert the next element .
- Check for the b_fact each node.
- The b_fact of each node in this case is 0.
Step 4:
- Insert the next element 8.
- Check for the b_fact of each node.
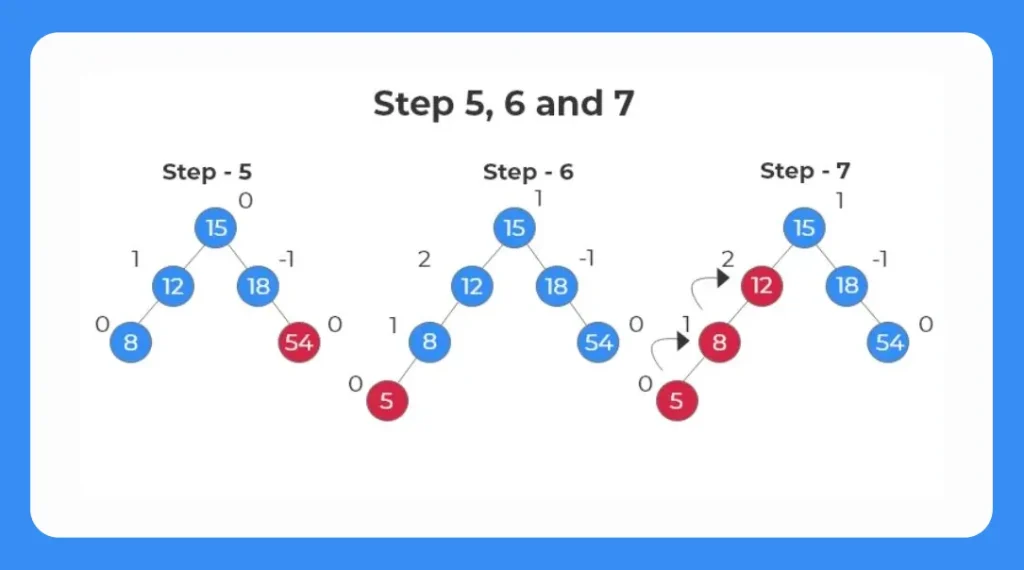
Step 5:
- Insert the next element 54.
- Check if the b_fact is anything other than -1 , 0 , 1.
Step 6:
- Insert the next element 5.
- Check the b_fact of each node.
- We can see the b_fact of the node 12 is 2. The tree becomes unbalanced.
- We have to balance the tree by identifying the rotation mechanism to be applied.
Step 7:
- We observe the element is inserted to the ,left of the left subtree.
- Thus we have to apply LL Rotation.
- The nodes involved in the rotation are shown in red.
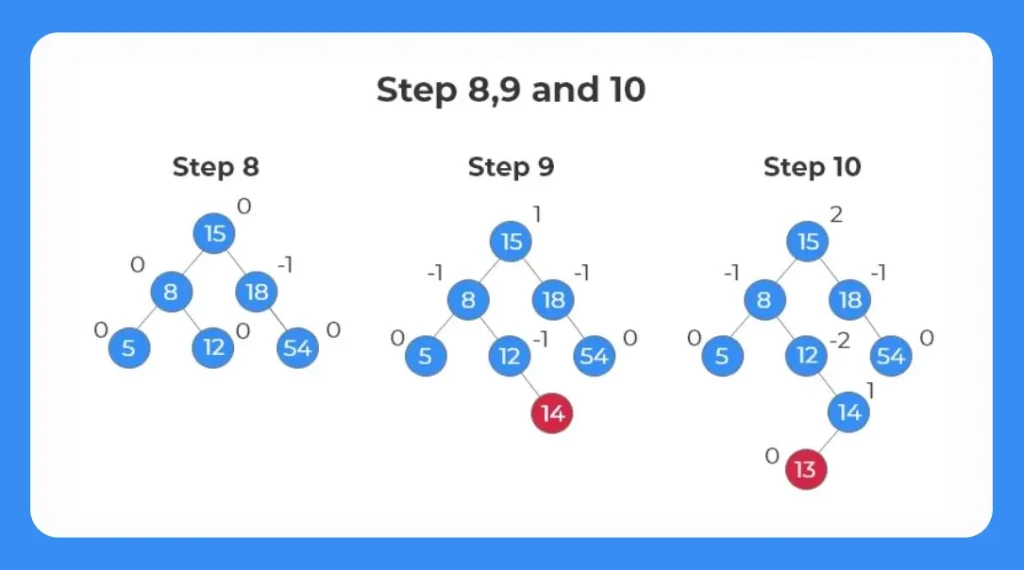
Step 8:
- In order to balance the tree, the tree is rotated towards the right.
- In this case the new parent is 8 and the nodes 5 and 12 becomes the child nodes.
Step 9:
- The next element inserted in the tree is 14.
- Again check the b_fact of each node of the tree.
Step 10:
- The next element to be inserted in the tree is 13.
- After the insertion of the new node, we check for the b_fact of each node.
- Now due to the latest insertion to the tree we can see that the balancing factor of multiple nodes is distorted
- We look for the first ancestor on which the balance factor is disturbed.
- We identify the rotation mechanism to be used.
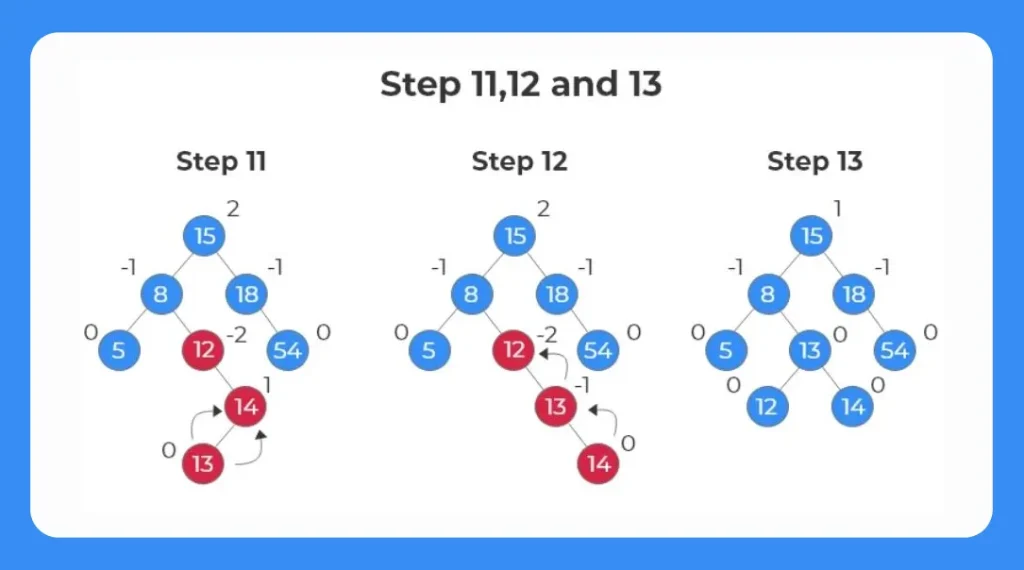
Step 11:
- To balance the tree we use the RL Rotation Mechanism.
- We identify the nodes that are involved in thre rotation mechanism which are shown in red.
Step 12:
- In this scenario, first a right rotation is applied.
- The tree after right rotation is shown as follows.
Step 13:
- Now to balance the tree, we apply a left rotation.
- After the rotation, the node 13 becomes the new parent node and the nodes 12 and 14 become the new child nodes.
- If we check the balance factor for each node, the balance factor is eithe 0 , 1 or -1.
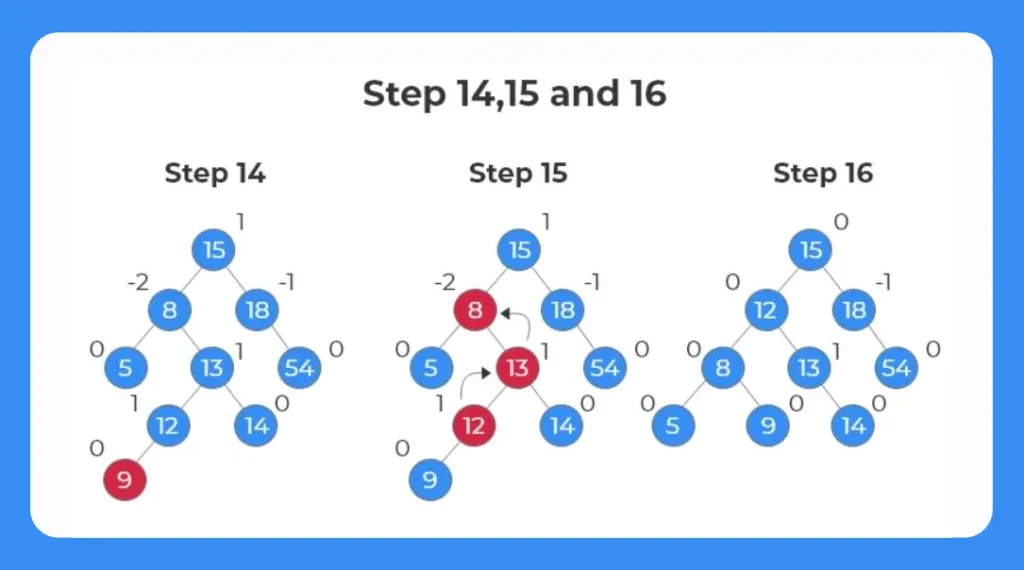
Step 14:
- The next element to be inserted is 9.
- As the new element is inserted, we observe that the balance factor of the node 8 becomes (-2).
Step 15:
- We can see from the image that for balancing the tree we need to apply RL Rotation.
- Again, first a right rotation is applied and then a left rotation is applied to the tree structure.
Step 16:
- After applying the RL Rotation, the tree structure with the optimal b_fact is shown as follows.
- We can see that the b_fact ranges between 0 , 1 and -1.
- Thus it is an AVL tree.
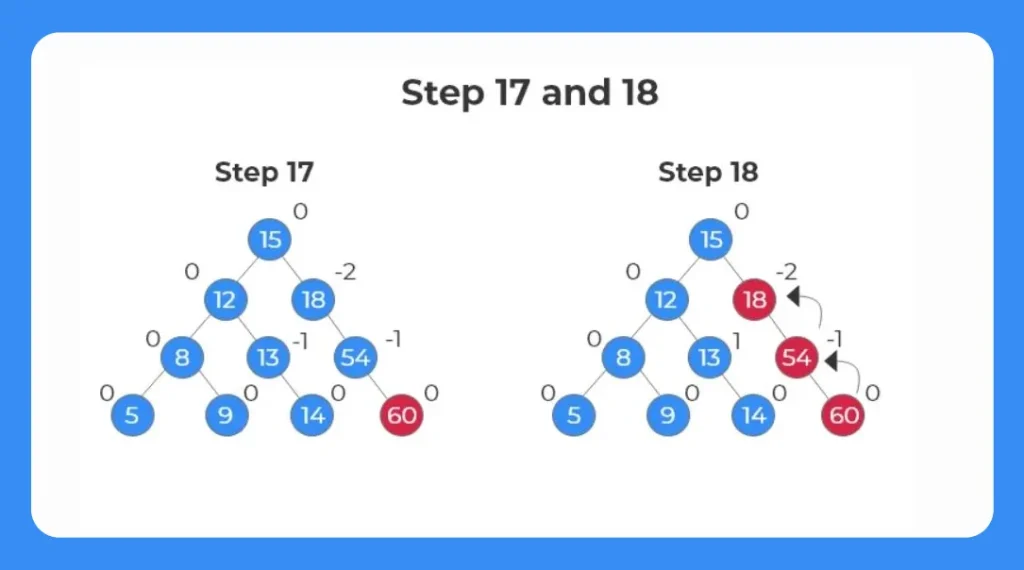
Step 17:
- The next element to be inserted is 60.
- As 60 is inserted the b_fact of the nodes of right subtree is disturbed.
Step 18:
- Since the disturbance in the balance factor is due to the insertion of an element to the right of the right subtree, we use RR Rotation.
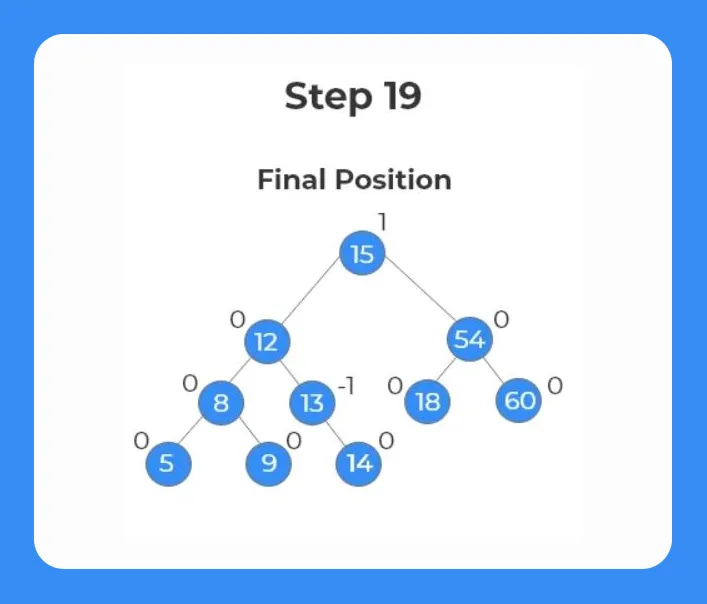
Step 19:
- After applying the RR Rotation the tree so obtained is shown below.
- All the nodes satisfy the condition of an AVL tree.
- The final tree at the end of insertion process with balanced nodes is shown below.
Code Implementation for Insertion in AVL Tree
#include<bits/stdc++.h>
using namespace std;
struct node
{
int element;
struct node *left,*right;
int ht;
};
node *insert(node *,int);
void preorder(node *);
void inorder(node *);
int height( node *);
node *rotateright(node *);
node *rotateleft(node *);
node *RR(node *);
node *LL(node *);
node *LR(node *);
node *RL(node *);
int balanceFactor(node *);
int main()
{
node *root=NULL;
int x,n,i,option;
do {
cout << “1. Create AVL Tree\n“;
cout << “2. End Program\n“;
cout << “Enter your choice “;
cin >> option;
switch(option)
{
case 1: cout << “\nEnter no. of elements : “;
cin >> n;
root = NULL;
for( i = 0; i < n;i++) {
cout << “Enter element of tree “;
cin >> x;
root = insert(root,x);
}
cout << “\nPreorder sequence:\n“;
preorder(root);
cout << “\n\nInorder sequence:\n“;
inorder(root);
break;
}
}while(option!=2);
return 0;
}
node * insert(node *T,int x)
{
if(T == NULL){
T = (node*)malloc(sizeof(node));
T -> element = x;
T -> left = NULL;
T -> right = NULL;
}
else
if(x > T->element)
{
T -> right = insert(T -> right,x);
if(balanceFactor(T) == –2)
if( x > T -> right -> element)
T = RR(T);
else
T = RL(T);
}
else
if(xelement)
{
T -> left = insert(T -> left,x);
if(balanceFactor(T)==2)
if(x < T-> left -> element)
T=LL(T);
else
T=LR(T);
}
T -> ht = height(T);
return(T);
}
int height(node *T)
{
int lh,rh;
if(T == NULL)
return(0);
if( T -> left == NULL)
lh = 0;
else
lh = 1 + T -> left -> ht;
if(T -> right == NULL)
rh = 0;
else
rh=1+T->right->ht;
if(lh > rh)
return(lh);
return(rh);
}
node * rotateright(node *x)
{
node *y;
y = x -> left;
x -> left = y -> right;
y -> right = x;
x -> ht = height(x);
y -> ht = height(y);
return(y);
}
node * rotateleft(node *x)
{
node *y;
y = x -> right;
x -> right = y -> left;
y -> left = x;
x -> ht = height(x);
y -> ht = height(y);
return(y);
}
node * RR(node *T)
{
T = rotateleft(T);
return(T);
}
node * LL(node *T)
{
T = rotateright(T);
return(T);
}
node * LR(node *T)
{
T -> left = rotateleft(T->left);
T = rotateright(T);
return(T);
}
node * RL(node *T)
{
T -> right = rotateright(T->right);
T = rotateleft(T);
return(T);
}
int balanceFactor(node *T)
{
int lh,rh;
if( T == NULL)
return(0);
if(T -> left == NULL)
lh = 0;
else
lh = 1 + T->left->ht;
if(T -> right == NULL)
rh = 0;
else
rh = 1 + T -> right -> ht;
return(lh-rh);
}
void preorder(node *T)
{
if( T != NULL)
{
cout << “Balance factor “ << T -> element << ” “ << balanceFactor(T) << endl;
preorder(T->left);
preorder(T->right);
}
}
void inorder(node *T)
{
if( T != NULL)
{
inorder(T->left);
cout << “Balance Factor “< element<<” “ << balanceFactor(T) << endl;
inorder(T->right);
}
}
Output: 1. Create AVL Tree 2. End Program Enter your choice 1 Enter no. of elements : 10 Enter element of tree 15 Enter element of tree 18 Enter element of tree 12 Enter element of tree 8 Enter element of tree 54 Enter element of tree 5 Enter element of tree 14 Enter element of tree 13 Enter element of tree 9 Enter element of tree 60 Preorder sequence: Balance factor 15 1 Balance factor 12 0 Balance factor 8 0 Balance factor 5 0 Balance factor 9 0 Balance factor 13 -1 Balance factor 14 0 Balance factor 54 0 Balance factor 18 0 Balance factor 60 0 Inorder sequence: Balance Factor 5 0 Balance Factor 8 0 Balance Factor 9 0 Balance Factor 12 0 Balance Factor 13 -1 Balance Factor 14 0 Balance Factor 15 1 Balance Factor 18 0 Balance Factor 54 0 Balance Factor 60 0 1. Create AVL Tree 2. End Program Enter your choice 2
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others






Login/Signup to comment