Pythagorean Triplet in an Array in Java
Pythagorean Triplet in Java
Problem of finding a Pythagorean Triplet in an Array in Java is a classic question often asked in coding interviews and algorithm challenges. It is based on the mathematical concept of the Pythagoras Theorem, which relates the sides of a right angled triangle. This problem tests your understanding of number manipulation, searching, and sorting techniques in arrays.
In this article, we will understand what a Pythagorean triplet means, explore different approaches to find such triplets in an array, analyze their complexities, and write complete Java programs with clear explanations.

What is Pythagorean Triplet?
Pythagorean Triplet consists of three integers (a, b, c) such that:
a2+b2=c2
For example:
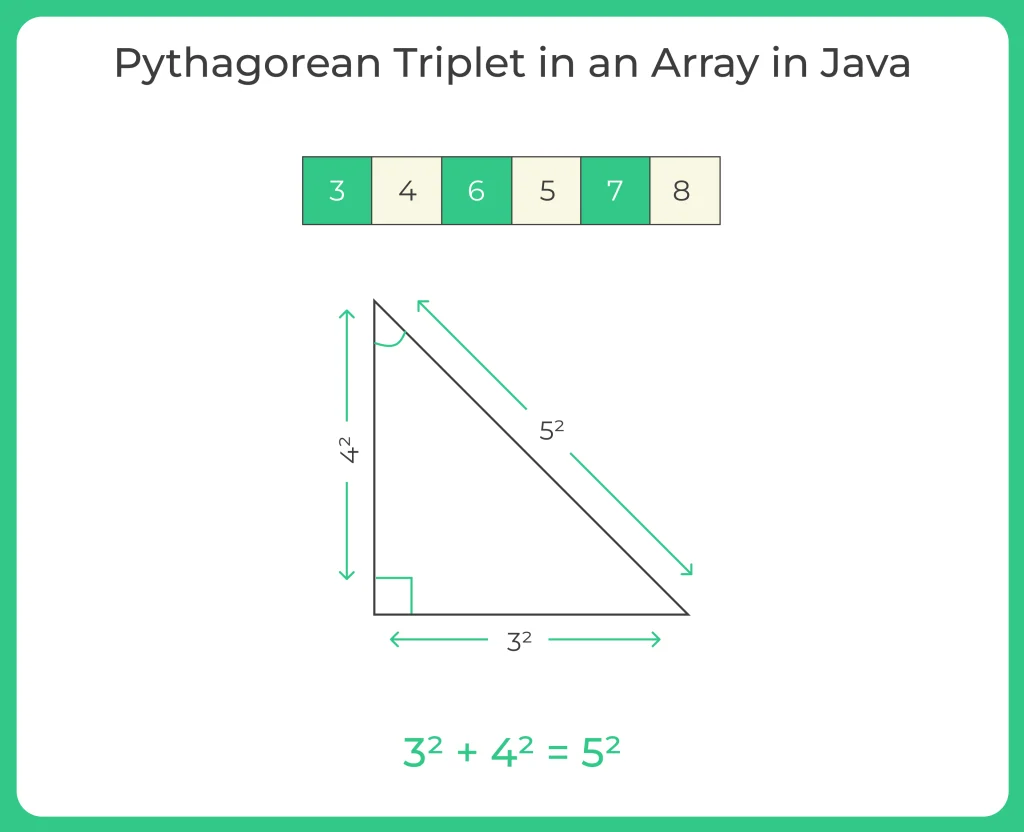
- (3, 4, 5) → 32 + 42 = 9 + 16 = 25 = 52
- (5, 12, 13) → 52 + 122 = 25 + 144 = 169 = 132
Our goal is to check whether any three numbers in the given array form a Pythagorean Triplet.
Problem Statement for Pythagorean Triplet in an Array:
Given an array of integers, determine if there exist any three elements a, b, c in the array such that:
a2+b2=c2
Example:
Input:
arr = {3, 1, 4, 6, 5}Output:
Yes, Pythagorean triplet exists (3, 4, 5)
Method to find out Pythagorean Triplet in an Array:
Here we have mentioned 3 methods to find Pythagorean Triplet in an array in java programming language:
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Approach 1: Brute Force Method
Algorithm for finding Pythagorean Triplet using Brute Force Method:
- Traverse through all possible triplets (i, j, k) using three nested loops.
- For each combination, check if arr[i]2 + arr[j]2 = arr[k]2
- If found, print the triplet and return true.
- If no such triplet exists after checking all combinations, return false.
Code In Java:
public class PythagoreanTriplet {
static boolean isTriplet(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
int x = arr[i] * arr[i];
int y = arr[j] * arr[j];
int z = arr[k] * arr[k];
if (x + y == z || y + z == x || z + x == y) {
System.out.println("Triplet found: " + arr[i] + ", " + arr[j] + ", " + arr[k]);
return true;
}
}
}
}
return false;
}
public static void main(String[] args) {
int[] arr = {3, 1, 4, 6, 5};
if (!isTriplet(arr))
System.out.println("No Pythagorean Triplet Found.");
}
}
Output:
Triplet found: 3, 4, 5
Space Complexity: O(1)
Approach 2: Sorting and Two Pointer Method
Algorithm for finding Pythagorean Triplet using Sorting and Two Pointer Method:
This is an optimized approach based on sorting and the two pointer technique.
- Square all elements in the array.
- Sort the array in ascending order.
- For each element (considered as c²), use two pointers (left and right) to find if there exist two numbers whose sum equals that element.
If arr[left] + arr[right] == arr[i], a triplet is found.
If the sum is smaller, move left++.
If the sum is larger, move right–.
Code In Java:
import java.util.Arrays;
public class PythagoreanTripletEfficient {
static boolean isTriplet(int[] arr) {
int n = arr.length;
// Step 1: Square all elements
for (int i = 0; i < n; i++) { arr[i] = arr[i] * arr[i]; } // Step 2: Sort the array Arrays.sort(arr); // Step 3: Fix one element and use two-pointer technique for (int i = n - 1; i >= 2; i--) {
int left = 0;
int right = i - 1;
while (left < right) {
if (arr[left] + arr[right] == arr[i]) {
System.out.println("Triplet found: " +
(int)Math.sqrt(arr[left]) + ", " +
(int)Math.sqrt(arr[right]) + ", " +
(int)Math.sqrt(arr[i]));
return true;
}
if (arr[left] + arr[right] < arr[i])
left++;
else
right--;
}
}
return false;
}
public static void main(String[] args) {
int[] arr = {3, 1, 4, 6, 5};
if (!isTriplet(arr))
System.out.println("No Pythagorean Triplet Found.");
}
}
Output:
Triplet found: 3, 4, 5
Space Complexity: O(1)
Note: It reduces three nested loops to two, making it suitable for large inputs.
Approach 3: Using Hashing
Algorithm for finding Pythagorean Triplet using Hashing Method:
- Square all elements.
- Store all squares in a HashSet.
- For each pair (a, b), check if (a² + b²) exists in the set.
- If yes, print triplet.
Code In Java:
import java.util.HashSet;
public class PythagoreanTripletHashing {
static boolean isTriplet(int[] arr) {
int n = arr.length;
HashSet squares = new HashSet<>();
for (int num : arr)
squares.add(num * num);
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int sum = arr[i] * arr[i] + arr[j] * arr[j];
if (squares.contains(sum)) {
System.out.println("Triplet found: " + arr[i] + ", " + arr[j] + ", " + (int)Math.sqrt(sum));
return true;
}
}
}
return false;
}
public static void main(String[] args) {
int[] arr = {10, 4, 6, 12, 5, 13};
if (!isTriplet(arr))
System.out.println("No Pythagorean Triplet Found.");
}
}
Output:
Triplet found: 5, 12, 13
Space Complexity: O(n)
Note: This is often faster in practice because hash lookups are O(1) on average.
Comparison of all methods:
| Approach | Technique Used | Time Complexity | Space Complexity | Efficiency |
|---|---|---|---|---|
| 1 | Brute Force | O(n³) | O(1) | Low |
| 2 | Sorting + Two Pointers | O(n²) | O(1) | High |
| 3 | Hashing | O(n²) | O(n) | High |
Finding a Pythagorean Triplet in an Array in Java helps improve understanding of both mathematical logic and array manipulation.
- For small arrays, a brute force approach is fine, but for larger arrays, the sorting + two pointer or hashing method is much more efficient.
- This is a common coding interview problem that evaluates your ability to transform mathematical problems into optimized programming solutions.
FAQ's related to Pythagorean Triplet in an Array in Java
Answer:
A Pythagorean Triplet is a set of three positive integers (a, b, c) such that a2+b2=c2
These numbers represent the sides of a right angled triangle.
Answer:
Yes. There can be multiple valid triplets in an array, e.g., in {3, 4, 5, 6, 8, 10}, both (3, 4, 5) and (6, 8, 10) are valid triplets.
Answer:
Sorting and two pointer method is usually the best as it offers a good balance of simplicity and performance with O(n²) time and O(1) space.
Answer:
Since squaring the negative number always gives positive number. Negative numbers don’t affect the logic.
Answer:
They are used in geometry, computer graphics, physics simulations, and 3D distance calculations.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others







Login/Signup to comment