Boyer Moore Majority Vote Algorithm in Java
Boyer Moore Majority Vote Algorithm with Java
In this article, we will explore the Boyer Moore Majority Vote Algorithm and its implementation in Java.
This algorithm is known for its efficiency in identifying the majority element within an array, an element that appears more than half the time in the array’s total length. It operates in linear time and uses constant space, making it highly optimized for such tasks.
We’ll dive into the underlying logic of the algorithm and provide a detailed Java code example to help you understand how it works in practice.
Boyer Moore Majority Vote Algorithm in Java
Boyer Moore Majority Vote Algorithm in Java
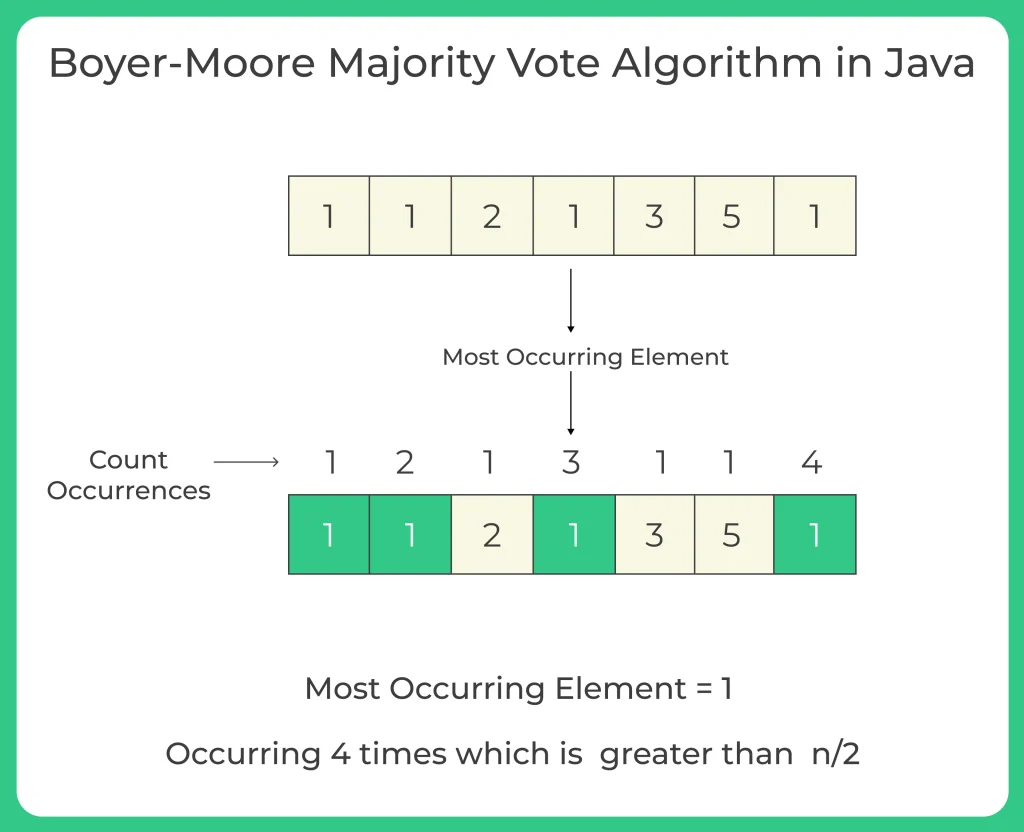
Boyer Moore Majority Vote Algorithm is a powerful and efficient algorithm used to find the majority element in an array. A majority element is defined as an element that appears more than n/2 times in an array of size n.
- Boyer Moore Majority Vote Algorithm operates in linear time complexity, which makes it efficient for large arrays, and uses constant space.
- Basic idea of the algorithm is to maintain a counter that starts from zero and iterates through the array, incrementing the counter for each occurrence of a candidate element, and decrementing it for each occurrence of a different element.
- Algorithm identifies the majority element as the candidate element with the highest count after scanning through the array.
This algorithm is particularly valued for its linear time complexity and constant space complexity, making it an optimal solution for large datasets.
Example Problem Statement:
Given an array of size n, find the majority element. The majority element is the element that appears more than n/2 times.
It is assumed that the input array always contains a majority element.
Input: [2, 2, 1, 1, 2, 2, 2] Output: 2
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Explaining Boyer Moore Majority Vote Algorithm
The algorithm works in two phases:
Phase 1: Find a Candidate
- Traverse the array while maintaining a candidate and a count.
- If the count is 0, set the current element as the candidate and set count to 1.
- If the current element is the same as the candidate, increment the count.
- If it’s different, decrement the count.
This works because the majority element will remain as the final candidate due to its higher frequency.
Phase 2: Verify the Candidate (Optional)
After determining the candidate, verify it by counting its occurrences in the array.
Algorithm for Boyer Moore Majority Vote
Step by step Procedure:
Initialize
count = 0,candidate = NoneTraverse the array
If
count == 0, setcandidate = current elementIf
candidate == current element, incrementcountElse, decrement
count
(Optional) Verify the candidate by counting its frequency
Java Code
public class BoyerMooreMajority {
// Function to find the majority element
public static int findMajorityElement(int[] nums) {
int count = 0;
int candidate = 0;
// Phase 1: Finding a candidate
for (int num : nums) {
if (count == 0) {
candidate = num;
}
count += (num == candidate) ? 1 : -1;
}
// Optional Phase 2: Verify the candidate
count = 0;
for (int num : nums) {
if (num == candidate) {
count++;
}
}
if (count > nums.length / 2) {
return candidate;
} else {
throw new IllegalArgumentException("No majority element found");
}
}
public static void main(String[] args) {
int[] nums = {2, 2, 1, 1, 2, 2, 2};
System.out.println("Majority element is: " + findMajorityElement(nums));
}
}
Output
The majority element is: 2
Space Complexity: O(1)
Why It Works ?
The Boyer Moore algorithm relies on the fact that a majority element occurs more than half the time. This means that all the other elements combined cannot cancel out its presence in the voting process.
Even if the array includes multiple elements with high frequencies, the one with more than half the total count will dominate the vote.
Applications:
- Finding majority elements in polling data.
- Stream processing algorithms.
- Simplified majority checks in real time systems.
Limitations
- Assumes that a majority element always exists.
- If the assumption doesn’t hold, the result from Phase 1 may not be valid unless verified in Phase 2.
To wrap it up....
The Boyer Moore Majority Vote Algorithm is a brilliant example of how a simple voting mechanism can solve a seemingly complex problem in linear time with constant space.
It is a must know for anyone preparing for coding interviews or working with large datasets where efficiency matters.
Always remember to verify the result if the presence of a majority element is not guaranteed…..
FAQ's related to Boyer Moore Majority Vote
Answer:
Boyer Moore Majority Vote Algorithm is an efficient method used to find the majority element in an array, an element that appears more than n/2 times.
It works in linear time (O(n)) and uses constant space (O(1)), making it ideal for large datasets.
Answer:
It uses a candidate and a count. As it scans the array, it increases the count when the current element matches the candidate and decreases it otherwise. When the count reaches zero, it updates the candidate. The idea is that non majority elements cancel each other out, leaving the majority element as the final candidate.
Answer:
Algorithm assumes that a majority element does exist. If that is not guaranteed, a second pass through the array is required to verify that the candidate occurs more than n/2 times.
Answer:
The original Boyer Moore algorithm only finds one majority element (> n/2). However, an extension of the algorithm can be used to find all elements appearing more than n/3 times, by tracking two candidates instead of one.
Answer:
Unlike other approaches that may use hash maps or extra arrays, Boyer Moore only uses a couple of variables (a candidate and a counter), which means it requires only constant memory regardless of input size.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others







else {
i–;
}
wont it be i–;?