K Pairs with smallest sum in two arrays in Java
K-pairs with smallest sum in two arrays
In this article we will explore problem, K pairs with smallest sum in two arrays in Java along with simple explanations, multiple approaches, time and space complexity analysis, and a complete working solution.
In coding interviews and real world applications, problems involving two arrays and their combinations are quite common. One such problem is finding the k pairs with the smallest sums from two sorted or unsorted arrays. This problem not only tests your understanding of basic array manipulation but also introduces you to advanced techniques like heaps (priority queues).

K pairs with smallest sum in two arrays in Java
Problem Statement:
Given two integer arrays nums1 and nums2 sorted in ascending order, and an integer k, return the k pairs (u, v) where u is from nums1 and v is from nums2 such that the sum u + v is the smallest possible among all combinations.
Input:
nums1 = [1, 7, 11] nums2 = [2, 4, 6] k = 3
Output:
[(1, 2), (1, 4), (1, 6)]
Explanation:
- The smallest sum pair is (1,2) → sum = 3
- Next is (1,4) → sum = 5
- Then (1,6) → sum = 7
- The rest have larger sums.
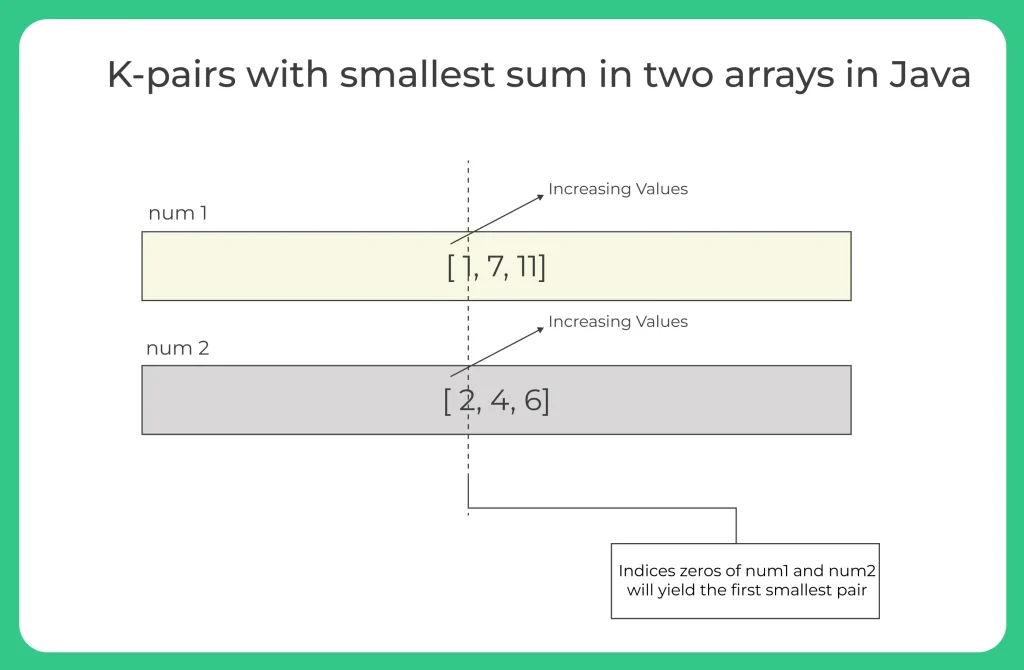

There are 2 ways to solve the problem, K pairs with smallest sum in two arrays in Java:
Use Case: Simple to implement; suitable only for small input sizes.
Use Case: Efficient for large arrays; avoids generating all pairs.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Method 1: Brute Force Approach for K pairs with smallest sum in two arrays
Algorithms:
- Generate all possible pairs from nums1 and nums2.
- Store them in a list along with their sums.
- Sort the list based on the sum.
- Return the first k pairs.
Where n = length of nums1, m = length of nums2
Space Complexity: O(n * m)
Java Code:
import java.util.*;
public class KSmallestPairsBruteForce {
public static List kSmallestPairs(int[] nums1, int[] nums2, int k) {
List allPairs = new ArrayList<>();
for (int a : nums1) {
for (int b : nums2) {
allPairs.add(new int[]{a, b});
}
}
allPairs.sort(Comparator.comparingInt(p -> p[0] + p[1]));
return allPairs.subList(0, Math.min(k, allPairs.size()));
}
public static void main(String[] args) {
int[] nums1 = {1, 7, 11};
int[] nums2 = {2, 4, 6};
int k = 3;
List result = kSmallestPairs(nums1, nums2, k);
for (int[] pair : result) {
System.out.println(Arrays.toString(pair));
}
}
}
Method 2: Min Heap Approach for K pairs with smallest sum in two arrays
Instead of generating all possible pairs, we use a Min Heap to keep track of the next smallest possible pair based on sum.
Algorithms:
Push the first element of nums1 paired with the first element of nums2 into the heap.
Keep pushing the next candidate pairs from nums2 for each element in nums1.
Extract the minimum sum pair k times.
Space Complexity: O(k)
Java Code:
import java.util.*;
public class KSmallestPairsHeap {
static class Pair {
int i, j; // indices in nums1 and nums2
Pair(int i, int j) {
this.i = i;
this.j = j;
}
}
public static List kSmallestPairs(int[] nums1, int[] nums2, int k) {
List result = new ArrayList<>();
if (nums1.length == 0 || nums2.length == 0 || k <= 0) return result;
PriorityQueue minHeap = new PriorityQueue<>(Comparator.comparingInt(p -> nums1[p.i] + nums2[p.j]));
for (int i = 0; i < Math.min(k, nums1.length); i++) {
minHeap.add(new Pair(i, 0));
}
while (!minHeap.isEmpty() && result.size() < k) {
Pair current = minHeap.poll();
result.add(new int[]{nums1[current.i], nums2[current.j]});
if (current.j + 1 < nums2.length) {
minHeap.add(new Pair(current.i, current.j + 1));
}
}
return result;
}
public static void main(String[] args) {
int[] nums1 = {1, 7, 11};
int[] nums2 = {2, 4, 6};
int k = 3;
List result = kSmallestPairs(nums1, nums2, k);
for (int[] pair : result) {
System.out.println(Arrays.toString(pair));
}
}
}
Step by Step Explanation of Optimized Approach:
Let’s say:
nums1 = [1, 7, 11]
nums2 = [2, 4, 6]
k = 3
- Insert pairs: (1,2), (7,2), (11,2) into the min-heap.
- Extract (1,2) → sum = 3 → add to result.
- Push (1,4) (i.e., next pair with same i and j+1).
- Extract (1,4) → sum = 5 → add to result.
- Push (1,6).
- Extract (1,6) → sum = 7 → done.
Comparison of both methods:
| Approach | Time Complexity | Space Complexity | Use Case |
|---|---|---|---|
| Brute Force | O(n * m * log(n * m)) | O(n * m) | Small arrays, easy to implement |
| Min Heap | O(k * log k) | O(k) | Efficient for large arrays |
Conclusion….
K smallest pairs with sum problem is a classic case of using greedy techniques with the help of a heap to optimize search. While brute force works for small data, using PriorityQueue helps scale the solution efficiently for large inputs. This problem also improves your grip on data structures and algorithmic thinking in Java.
Keep practicing problems like these to master combinations, sorting, and heaps!
FAQ's Related to K pairs with smallest sum in two arrays in Java
Answer:
Min heap (priority queue) is best suited for this problem as it helps efficiently extract the smallest sum pairs.
Answer:
Yes, but the optimized heap based approach assumes sorted arrays. For unsorted arrays, the brute force method or sorting them first is needed.
Answer:
In that case, just return all the possible pairs. Both approaches handle this with Math.min(k, total_pairs).
Answer:
No, you need to implement the logic using arrays and a priority queue as shown.
Answer:
The logic remains the same, duplicates will naturally be included based on the sum order. No extra steps needed unless specified.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java







import java.util.*;
public class Main {
public static void kSmallestPair(int[] A, int[] B,
int K)
{
int n = A.length;
// Min heap which contains tuple of the format
// (sum, (i, j)) i and j are the indices
// of the elements from array A
// and array B which make up the sum.
PriorityQueue pq
= new PriorityQueue((a, b) -> a[0] – b[0]);
// my_set is used to store the indices of
// the pair(i, j) we use my_set to make sure
// the indices does not repeat inside min heap.
Set mySet = new HashSet();
// initialize the heap with the minimum sum
// combination i.e. (A[0] + B[0])
// and also push indices (0,0) along
// with sum.
pq.offer(new int[] { A[0] + B[0], 0, 0 });
mySet.add(“0,0”);
// iterate upto K
int count = 0;
while (count < K && !pq.isEmpty()) {
// array format (sum, i, j).
int[] temp = pq.poll();
int i = temp[1], j = temp[2];
System.out.println(
"(" + A[i] + ", " + B[j]
+ ")"); // Extracting pair with least sum
// such that one element is from
// arr1 and another is from arr2
// check if i+1 is in the range of our first
// array A
boolean flag = false;
if (i + 1 < n) {
int sum = A[i + 1] + B[j];
// insert (A[i + 1] + B[j], i + 1, j)
// into min heap.
String key = (i + 1) + "," + j;
// insert only if the pair (i + 1, j) is
// not already present inside the set i.e.
// no repeating pair should be present
// inside the heap.
if (!mySet.contains(key)) {
pq.offer(new int[] { sum, i + 1, j });
mySet.add(key);
flag = true;
}
}
// check if j+1 is in the range of our second
// array B
if (j + 1 < B.length) {
// insert (A[i] + B[j + 1], i, j + 1)
// into min heap.
int sum = A[i] + B[j + 1];
String key = i + "," + (j + 1);
// insert only if the pair (i, j + 1)
// is not present inside the heap.
if (!mySet.contains(key)) {
pq.offer(new int[] { sum, i, j + 1 });
mySet.add(key);
flag = true;
}
}
if (!flag) {
break;
}
count++;
}
}
public static void main(String[] args)
{
int[] A = { 1 };
int[] B = { 2, 4, 5, 9 };
int K = 8;
kSmallestPair(A, B, K);
}
}
Join our Discord for technical queries.