0
Notifications Mark All Read
- Login
- Get Prime
Insertion in AVL Tree in Java
Insertion In AVL Tree
AVL tree is self balancing tree in which for all nodes, the difference of height between the left subtree and the right subtree is less than or equal to 1. In this article, an avl tree is created and the difference of height is printed for each node.

Why AVL tree?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that height of the tree remains O(Logn) after every insertion and deletion, then we can guarantee an upper bound of O(Logn) for all these operations. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree
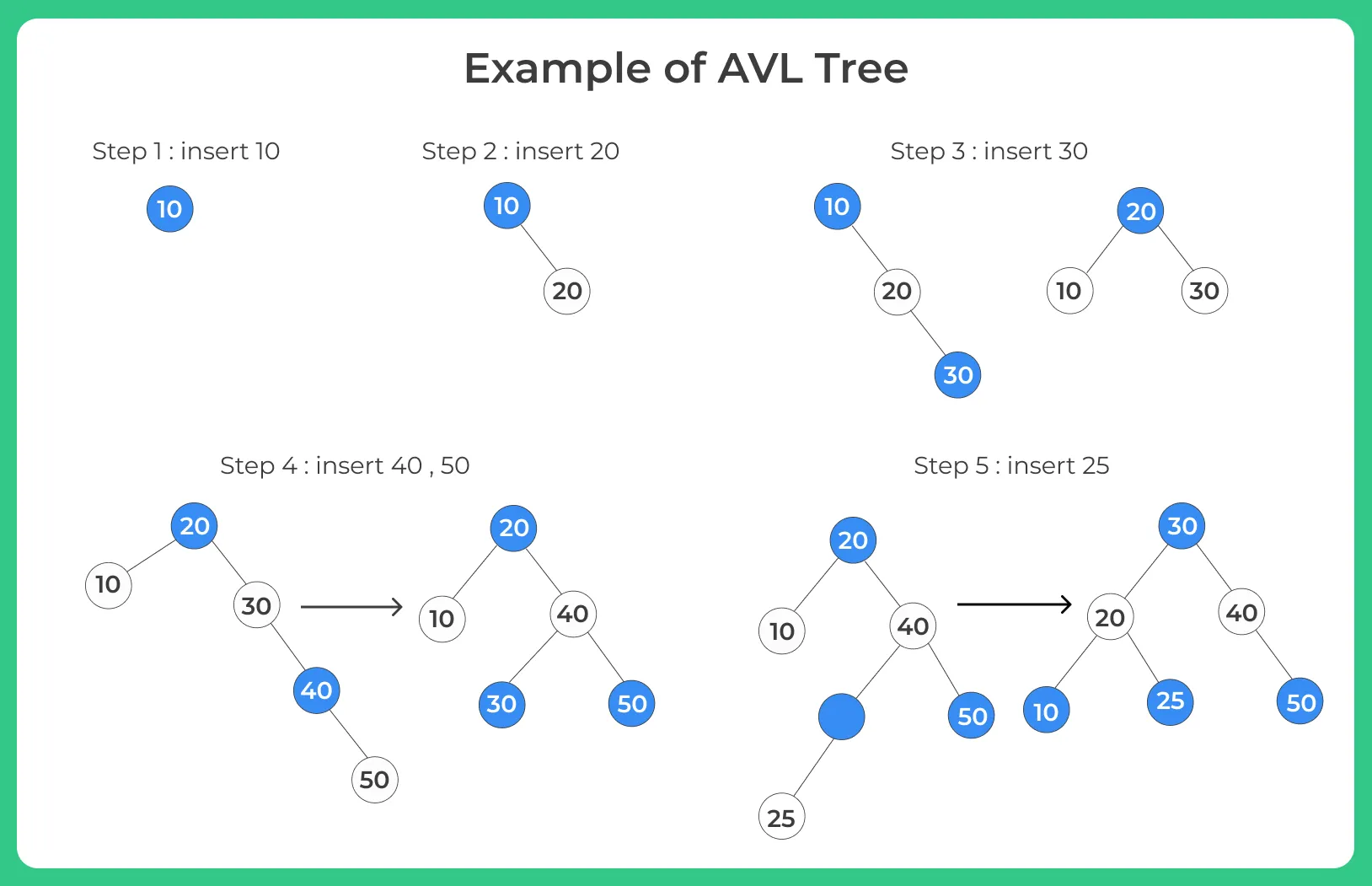
Insertion and Creation of an AVL Tree
- A new node can be inserted in an AVL tree by determining the correct position of the node. But insertion of a new node into the tree may affect the height of the tree and the tree might become unbalanced.
- If the new nodes are inserted as child nodes on a non- leaf node there will be no alteration since there will be no effect on the balancing as there is no increase in the height of the tree.
- If the new nodes are inserted as child nodes on a leaf node, the balancing of the tree might get distorted. This depends on whether the node is added to the left subtree or the right subtree.
- Thus to re-balance the tree in order to conserve it’s characteristics we use Rotation Mechanism. There are four types of rotations which help maintain the balancing of the tree as specified above.
- If, due to insertion,the b_fact of multiple nodes is disturbed, balancing occurs on the first ancestor of the node that has been inserted.
Note: During the process of insertion it is important to check the balancing factor of each node at each step, until the process end.
Steps for Creating AVL Tree :
Suppose we are given an AVL tree T and N is the new node to be inserted.
- Perform a standard BST insertion of node N in the AVL tree T.
- Starting from node N, traverse up until the first unbalanced node is not found. Let z be the first unbalanced node, y be the child of z that comes on the path from p to z and x be the grandchild of z that comes on the path from p to z.
- Rebalance the tree by performing suitable rotations on the subtree. There can be the following 4 possible cases and after choosing what case is it, we have to do appropriate rotation explained above.
- Left-Left Case – y is left child of z and x is left child of y
- Left-Right Case – y is left child of z and x is the right child of y
- Right-Right Case – y is the right child of z and x is the right child of y
- Right-Left Case – y is the right child of z and x is left child of y
Note: We only need to re-balance the subtree where the first imbalance has occurred using the above cased and the complete tree automatically becomes height-balanced.
import java.util.*;
class Node
{
int key, height;
Node left, right;
Node (int value)
{
key = value;
height = 1;
}
}
class AVLTree{
Node root;
int height (Node ptr)
{
if (ptr == null)
return 0;
return ptr.height;
}
int max (int a, int b)
{
return (a > b) ? a : b;
}
Node rotateRight (Node b)
{
Node a = b.left;
Node c = a.right;
a.right = b;
b.left = c;
b.height = max (height (b.left), height (b.right)) + 1;
a.height = max (height (a.left), height (a.right)) + 1;
return a;
}
Node rotateLeft (Node a)
{
Node b = a.right;
Node c = b.left;
b.left = a;
a.right = c;
a.height = max (height (a.left), height (a.right)) + 1;
b.height = max (height (b.left), height (b.right)) + 1;
return b;
}
int getBalance (Node ptr)
{
if (ptr == null)
{
return 0;
}
return height (ptr.left) - height (ptr.right);
}
Node insert (Node node, int key)
{
if (node == null)
return (new Node (key));
if (key < node.key)
node.left = insert (node.left, key);
else if (key > node.key)
node.right = insert (node.right, key);
else
return node;
node.height = 1 + max (height (node.left), height (node.right));
int balance = getBalance (node);
if (balance > 1 && key < node.left.key)
return rotateRight (node);
if (balance < -1 && key > node.right.key)
return rotateLeft (node);
if (balance > 1 && key > node.left.key)
{
node.left = rotateLeft (node);
return rotateRight (node);
}
if (balance < -1 && key < node.right.key)
{
node.right = rotateRight (node.right);
return rotateLeft (node);
}
return node;
}
void preOrder (Node ptr)
{
if (ptr != null)
{
System.out.print (ptr.key + " ");
preOrder (ptr.left);
preOrder (ptr.right);
}
}
}
public class Main{
public static void main (String[]args)
{
AVLTree tree = new AVLTree ();
tree.root = tree.insert (tree.root, 10);
tree.root = tree.insert (tree.root, 20);
tree.root = tree.insert (tree.root, 30);
tree.root = tree.insert (tree.root, 40);
tree.root = tree.insert (tree.root, 50);
tree.root = tree.insert (tree.root, 25);
System.out.println ("Tree Traversal");
tree.preOrder (tree.root);
}
}
Output:
Tree Traversal 30 20 10 25 40 50
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java

 0
0



Login/Signup to comment