Searching In A Binary Search Tree In C++
Searching In A Binary Search Tree
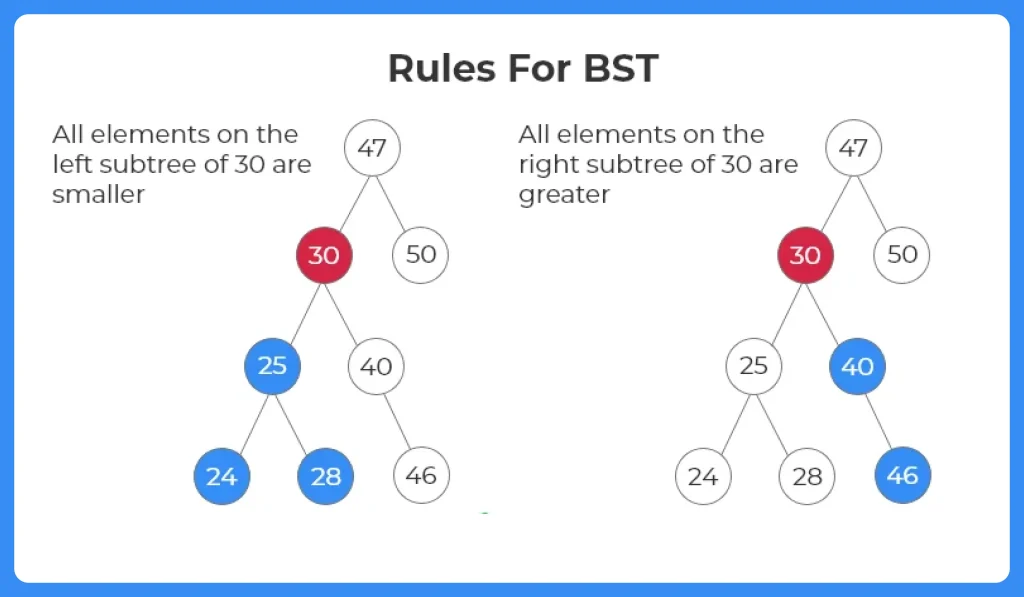
A binary search tree is a tree in which the data in the left subtree is less than the root and the data in the right subtree is greater than the root. Given a Binary Search Tree and a key, the task is to check whether the key is present in the tree or not. The search operation starts from the root and compares the key with the current node.
Based on the comparison, the search moves to either the left or right subtree, reducing the search space at each step. This process continues until the key is found or a null node is reached, making searching in a BST efficient and faster than in an unordered binary tree.

Prime Course Trailer
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Related Banners
Code Implementation of Binary Search Tree Program in C++
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
int data;
Tree *left = NULL, *right = NULL;
// Constructor initialised
Tree (int x)
{
data = x;
left = NULL;
right = NULL;
}
};
int search (Tree * root, int value)
{
while (root != NULL)
{
if (value > root->data)
root = root->right;
else if (value < root->data)
root = root->left;
else
return 1;
}
return 0;
}
void inorder_traversal (Tree * root)
{
if (root == NULL)
return;
inorder_traversal (root->left);
cout << root->data << " "; inorder_traversal (root->right);
}
Tree *insert_node (Tree * root, int x)
{
if (root == NULL)
{
Tree *temp = new Tree (x);
return temp;
}
if (root->data > x)
{
root->left = insert_node (root->left, x);
}
else
{
root->right = insert_node (root->right, x);
}
return root;
}
Tree *Delete (Tree * root, int x)
{
if (root == NULL)
{
cout << "Node not found "; return NULL; } if (root->data > x)
{
root->left = Delete (root->left, x);
}
else if (root->data < x) { root->right = Delete (root->right, x);
}
else
{
if (root->left == NULL)
{
Tree *temp = root->right;
free (root);
return temp;
}
else if (root->right == NULL)
{
Tree *temp = root->left;
free (root);
return temp;
}
else
{
Tree *temp = root->right;
while (temp->left != NULL)
temp = temp->left;
root->data = temp->data;
root->right = Delete (root->right, temp->data);
}
}
return root;
}
int main ()
{
Tree *root = new Tree (15);
root->left = new Tree (13);
root->right = new Tree (18);
root->left->left = new Tree (8);
root->left->right = new Tree (14);
root->right->left = new Tree (16);
root->right->right = new Tree (19);
int delete_item = 18;
cout << "Inorder Traversal :";
inorder_traversal (root);
cout << endl;
cout << endl;
cout << "17 inserted \n";
insert_node(root,17);
cout << "Inorder Traversal :";
inorder_traversal (root);
cout << endl;
cout << endl;
cout << "18 deleted \n";
Delete (root, delete_item);
cout << "Inorder Traversal :";
inorder_traversal (root);
cout << endl;
cout<< "Searching for element 15 \n";
cout << search (root, 15);
}
Output:
Inorder Traversal :8 13 14 15 16 18 19 17 inserted Inorder Traversal :8 13 14 15 16 17 18 19 18 deleted Inorder Traversal :8 13 14 15 16 17 19 Searching for element 15
Explanation:
- The Tree class defines a Binary Search Tree node that stores data and pointers to its left and right child nodes.
- The search() function checks whether a value exists in the BST by moving left or right based on comparisons.
- The insert_node() function adds a new value to the BST while maintaining BST properties using recursion.
- The Delete() function removes a node from the BST and correctly handles all three cases: leaf node, one child, and two children.
- The inorder_traversal() function prints the BST in sorted order, showing that the tree structure remains valid after insertion and deletion.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Search | O(h) | O(1) |
| Insertion | O(h) | O(h) |
| Deletion | O(h) | O(h) |
| Inorder Traversal | O(n) | O(h) |
| Overall | O(h) per operation | O(n) |
Conclusion:
Searching in a Binary Search Tree in C++ is an efficient operation that uses the structure’s inherent ordering to quickly determine whether a specific value exists in the tree. By starting at the root and comparing the target value with each node, the algorithm moves either to the left or right subtree based on whether the value is smaller or larger.
This approach significantly reduces the search space at every step. The implementation can be done iteratively or recursively, and it continues until the value is found or the subtree being searched becomes empty, indicating the value is not present. This makes BST search an effective and straightforward method for lookup operations in ordered tree data structures.
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment