Insertion in B-Tree in Java

March 26, 2026

Insertion in B-Tree

Insertion in a Binary Search Tree (BST) is one of the most important operations in data structures. It helps in building a sorted tree structure dynamically, which allows efficient searching and data organization.

In this article, we will understand how insertion works in a BST using Java, along with algorithm, examples, code, and practical insights.

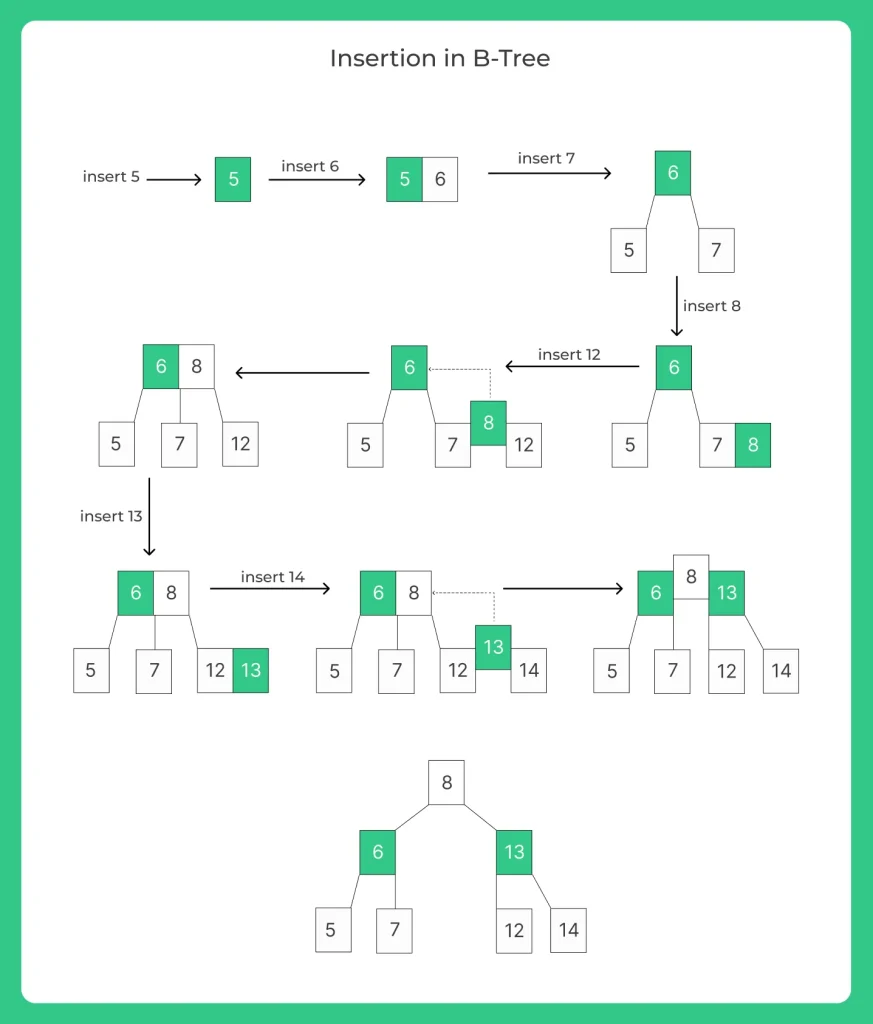
insertion in btree in java

Insertion in B-Tree in Java

What is a Binary Search Tree?

A Binary Search Tree (BST) is a binary tree where:

  • Left subtree contains values less than the node
  • Right subtree contains values greater than the node

This property makes operations like search, insertion, and deletion efficient.

Why is Insertion Important in BST?

Insertion is used to:

  • Build the tree dynamically
  • Maintain sorted data
  • Enable fast searching (O(log n) in balanced trees)
  • Support real world applications like indexing and searching

Rules for Insertion in BST:

While inserting a new value:

  1. Start from the root
  2. Compare the value with current node
  3. If smaller → move left
  4. If greater → move right
  5. Insert at the first empty position
Insertion in B-Tree
DSA mobile gif
DSA desktop gif

Algorithm for Insertion in B Tree in Java

Before practicing Insertion in Btree in java we have to analyze the Algorithm for Insertion in Btree mentioned as follows:

  1. If root is null, create a new node
  2. Compare key with root value
  3. If key < root → insert in left subtree
  4. If key > root → insert in right subtree
  5. Return the updated root

Inorder Tree Traversal in Binary Tree

Preorder Tree Traversal in Binary Tree

Postorder Tree Traversal in Binary Tree

Inorder Tree Traversal without Recursion

Preorder Tree Traversal without Recursion

Learn DSA

Learn DSA with Java

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Java Code for Insertion in B Tree in Java

Run 
class Node {
    int data;
    Node left, right;

    Node(int value) {
        data = value;
        left = right = null;
    }
}

public class BSTInsertion {

    public static Node insert(Node root, int key) {
        if (root == null) {
            return new Node(key);
        }

        if (key < root.data) {
            root.left = insert(root.left, key);
        } else if (key > root.data) {
            root.right = insert(root.right, key);
        }

        return root;
    }

    public static void inorder(Node root) {
        if (root != null) {
            inorder(root.left);
            System.out.print(root.data + " ");
            inorder(root.right);
        }
    }

    public static void main(String[] args) {
        Node root = null;

        int[] values = {50, 30, 70, 10, 40, 60, 90};

        for (int val : values) {
            root = insert(root, val);
        }

        System.out.print("Inorder Traversal: ");
        inorder(root);
    }
}

Input:

Insert → 50, 30, 70, 10, 40, 60, 90

Output:

Inorder Traversal → 10 30 40 50 60 70 90

Common Insights on Insertion in BTree

Edge Cases:

  • Inserting into an empty tree
  • Duplicate values (ignored or handled separately)
  • Highly unbalanced trees
  • Invalid input

Keep in mind that:

  • BST insertion is similar to binary search
  • Tree height directly affects performance
  • Inorder traversal always gives sorted output
  • Balanced BSTs improve efficiency

Best Practices:

  • Avoid duplicates unless required
  • Use iterative approach for large datasets
  • Validate inputs before insertion
  • Prefer self balancing trees (AVL/Red Black) in production

Frequently Asked Questions

Answer:

Insertion In Binary Search Tree In Java is the process of adding a new node into a BST while maintaining its sorted structure, where left nodes are smaller and right nodes are larger.

Answer:

Insertion starts from the root, compares values, moves left or right accordingly, and inserts the node at the first available null position.

Answer:

The time complexity is O(log n) in a balanced tree and O(n) in the worst case when the tree becomes skewed.

Answer:

It is used in databases, search engines, file systems, and applications where sorted data storage and fast lookup are required.

Answer:

Duplicates are usually ignored or handled using custom rules like storing counts or inserting consistently on one side.

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java