Tree Traversals: Depth First Search (DFS)

August 7, 2025

Tree Traversals: Depth First Search (DFS)

Tree traversal means visiting all the nodes of a tree in a specific order. One of the most common ways to do this is called Depth First Search (DFS). In DFS, we start from the root node and explore as far as possible along each branch before backtracking. This method helps us go deep into the tree structure first and then move sideways. DFS is mainly used in three types of tree traversals: Inorder, Preorder, and Postorder.

The term traversal means to visit each node in a tree exactly once. In linear lists the order of traversal is vividly first to last. However, in trees there exists no such natural linear order.In this article, depth first search is studied.

Tree Traversals - Depth First Search (DFS)

More Information About DFS:

DFS can be defined as an algorithm, based on backtracking, dedicated to traversing a tree structure by first visiting the root first and then the left sub-tree and the right sub-tree.

  • It is of three types:

    • In-order traversal.

    • Pre-order traversal.

    • Post-order traversal.

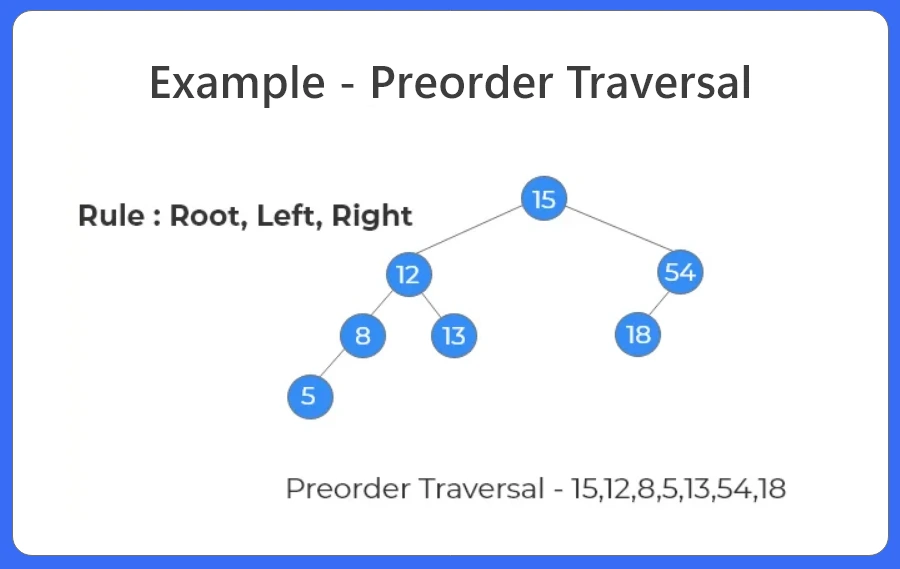
Preorder Traversal:

For traversal of a non-empty binary tree or binary search tree in Pre-order, following sequence of operations is performed.

  1. Visit the root node.
  2. Traverse the left sub tree in pre-order.
  3. Traverse the right sub tree in post-order.
Preorder Tree Traversal in binary tree in C++
Preorder Tree Traversal in binary tree in C++

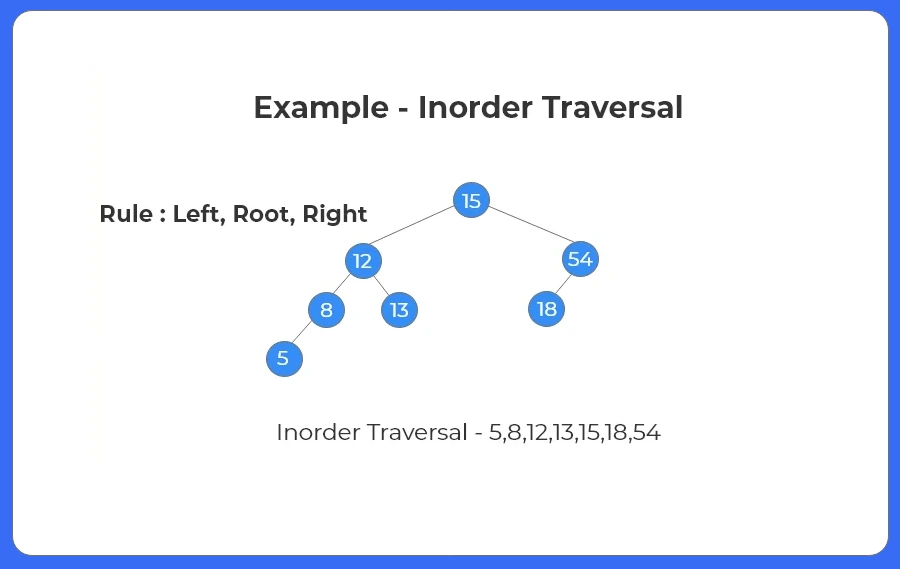
Inorder Traversal:

For traversal of a non-empty binary tree or binary search tree in In-order, following sequence of operations is performed.

  1. Traverse the left sub tree in in-order.
  2. Visit the root node.
  3. Traverse the right sub tree in in-order.
Inorder Tree traversal in binary tree in cpp
Inorder Tree traversal in binary tree in cpp

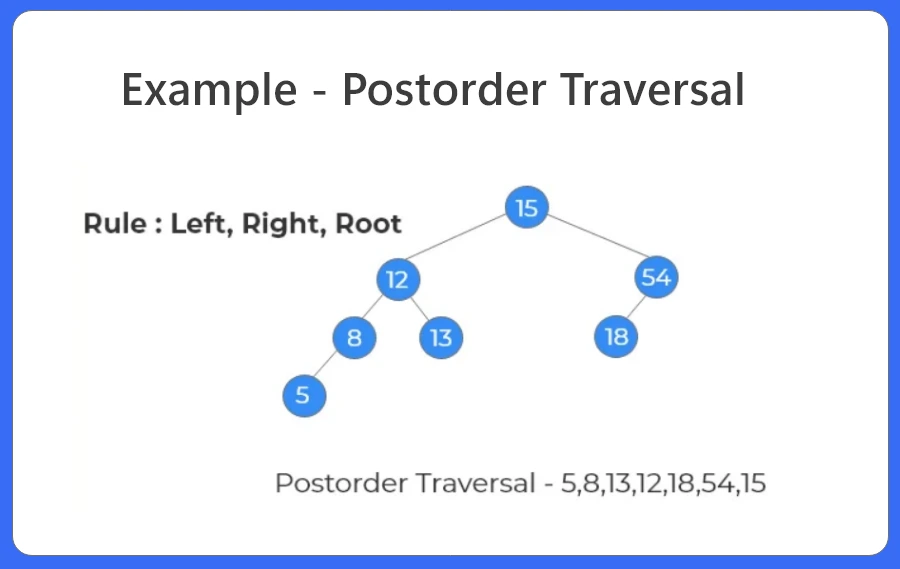
Postorder Traversal:

For traversal of a non-empty binary tree or binary search tree in Post-order, following sequence of operations is performed.

  1. Traverse the left sub tree in post-order.
  2. Traverse the right sub tree in post-order.
  3. Visit the root node.
postorder-tree-traversal-in-binary-tree
postorder-tree-traversal-in-binary-tree
DSA desktop gif
DSA mobile gif

BST: Search in a Binary Search Tree

BST: Insertion in a Binary Search Tree

BST: Deletion in a Binary Search Tree

Traversals in Tree

Tree Traversals: Breadth First Search (DFS)

Code Implementation for Tree Traversal : Depth-First Search (DFS) in C++

Run 
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};
void preorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Print the data
  cout << root->data << " "; // Visit Left subtree preorder_traversal (root->left);
  // Visit right subtree
  preorder_traversal (root->right);
}

void inorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Visit Left subtree
  inorder_traversal (root->left);
  // Print the data
  cout << root->data << " "; // Visit right subtree inorder_traversal (root->right);
}

void postorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  // Visit Left subtree
  postorder_traversal (root->left);
  // Visit right subtree
  postorder_traversal (root->right);
  // Print the data
  cout << root->data << " "; } int main () { Tree *root = new Tree (17); root->left = new Tree (10);
  root->right = new Tree (11);
  root->left->left = new Tree (7);
  root->right->left = new Tree (27);
  root->right->right = new Tree (9);
  cout << "Preorder => ";
  preorder_traversal (root);
  cout << endl;
  cout << "Inorder => ";
  inorder_traversal (root);
  cout << endl;
  cout << "Postorder => ";
  postorder_traversal (root);
  cout << endl;
  return 0;
}

Output:

Preorder => 17 10 7 11 27 9 
Inorder => 7 10 17 27 11 9 
Postorder => 7 10 27 9 11 17

Conclusion

Depth First Search (DFS) is a powerful and simple method to explore all the nodes of a tree. By following different DFS techniques like Inorder, Preorder, and Postorder, we can visit each node in a specific order depending on the need of the problem. These traversals are very useful in solving many coding problems, such as expression tree evaluation, file system navigation, and more.

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

FAQs - Depth First Search (DFS) Traversal

FAQs - Depth First Search (DFS) Traversal

In N-ary trees, each node can have more than two children. DFS traversal still follows the same depth-first strategy, but instead of checking just left and right, we loop through all children of a node. The logic is similar, but implementation must handle a list of children instead of fixed left/right pointers.

Yes, DFS traversals can be done without recursion using an explicit stack:

  • Preorder: Use a stack to process root → left → right.
  • Inorder: Use a stack to traverse leftmost nodes first, then visit root, then right.
  • Postorder: It’s the trickiest; either use two stacks or modify preorder logic and reverse the result.

DFS is preferred when:

  • You want to explore all paths deeply (e.g., maze solving, backtracking).
  • You need to perform topological sorting in trees or graphs.
  • Tree is very deep, and not very wide (to save space).
  • You are working on problems involving recursion or subtree-based calculations like diameter, sum, or path count.

Morris Traversal is a space-optimized method to perform Inorder traversal without using recursion or a stack.

  • It modifies the tree temporarily by creating threaded links between nodes.
  • It still follows the DFS approach but reduces space complexity to O(1).
    However, it’s complex to implement and not suitable when tree modification isn’t allowed.

The order of DFS traversal changes the meaning of the output:

  • Preorder: Useful in copying trees or prefix expression generation.
  • Inorder: Retrieves elements in sorted order (in BSTs).
  • Postorder: Used in deleting trees or evaluating postfix expressions.
    Choosing the correct traversal is crucial based on what you want from the tree structure.

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout