Deletion In Binary Search Tree In C++

February 3, 2026

Deletion In Binary Search Tree:

A binary search tree is a tree in which the data in left subtree is less than the root and the data in right subtree is greater than the root. There are three cases in deletion .In this article, deletion is performed in C++.

Deletion in a Binary Search Tree is more complex than insertion because removing a node can affect the overall structure of the tree. To maintain the BST properties, deletion is handled using three specific cases based on the number of children of the node being removed. These cases are explained and implemented using C++.

Three Possible Cases In Deletion:

The node to be deleted has no children.
The node to be deleted has 2 children.
The node to be deleted has 1 child.
In this example, 8, 13 and 18 are going to be deleted.

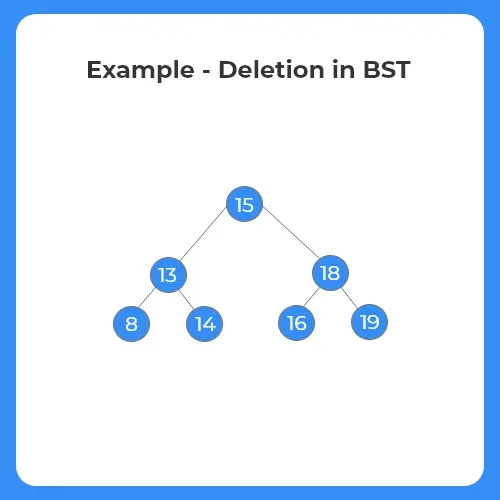
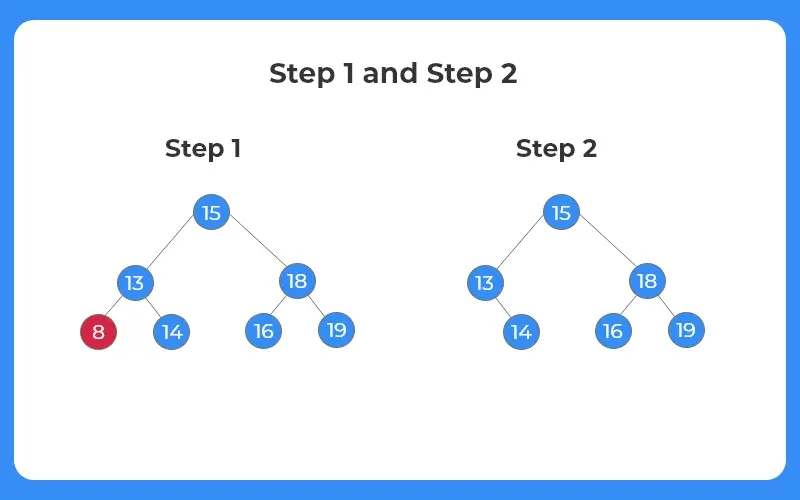
Case 1: The node to be deleted has no child nodes.

If the node to be deleted from the tree has no child nodes, the node is simple deleted from the tree since it is a leaf node.

Step 1:

The node to be deleted is 8.

Step 2:

Since the node 8 is a leaf node consisting of no child nodes, it is simply removed from the tree.
The BST structure after deletion is shown as follows.

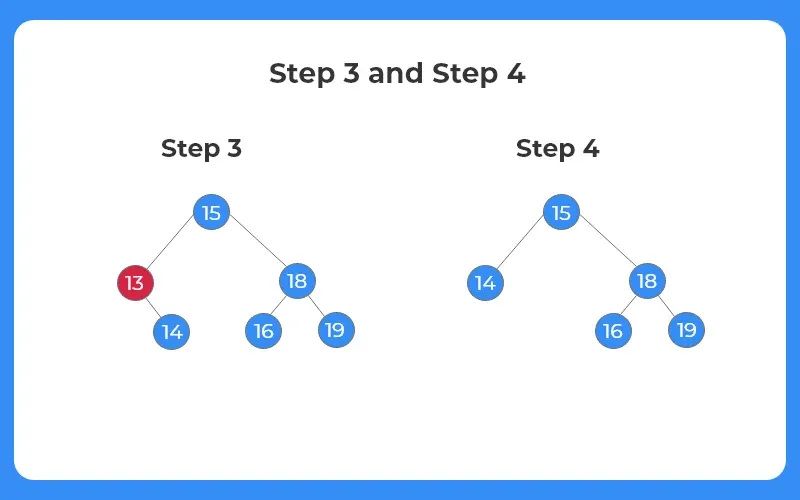
Case 2: The node to be deleted has a single child node

If the node to be deleted has a single child node, the target node is replaced from its child node and then the target node is simply deleted.

Step 3:

The node to be deleted is 13.

Step 4:

Since the target node has a single child, i.e, 14, we replace the node 13 with node 14.
The BST structure after deletion is shown as follows.

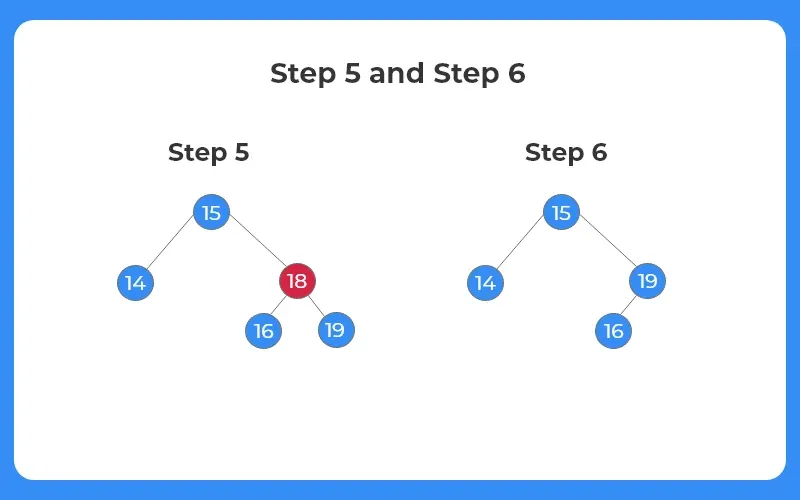
Case 3: The node to be deleted has two child nodes

If the node to be deleted has two child nodes, we first find the inorder successor of the node and replace the target node with the inorder successor.

Step 5:

The next node to be deleted is 18.

Step 6:

We can see from the image given that the target node 18 has two child nodes.
We find the inorder successor of the target node. In this case the inorder successor is 19. Inorder successor can be defined as the smallest element of the right subtree.
After replacing the target node with the inorder successor, the node is simply deleted.
The final BST is shown as follows

Binary Search Trees in Data Structure(Introduction)

Introduction to Binary Search Tree

BST: Search in a Binary Search Tree

BST: Insertion in a Binary Search Tree

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Code Implementation for Deletion in a Binary Search Tree in C++

Run

#include<bits/stdc++.h>
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};

Tree *Delete (Tree * root, int x)
{

  if (root == NULL)
    {
      cout << "Node not found "; return NULL; } if (root->data > x)
    {
      root->left = Delete (root->left, x);
    }

  else if (root->data < x) { root->right = Delete (root->right, x);
    }
  else
    {

      if (root->left == NULL)
	{
	  Tree *temp = root->right;
	  free (root);
	  return temp;
	}

      else if (root->right == NULL)
	{
	  Tree *temp = root->left;
	  free (root);
	  return temp;
	}
      else
	{

	  Tree *temp = root->right;

	  while (temp->left != NULL)
	    temp = temp->left;

	  root->data = temp->data;

	  root->right = Delete (root->right, temp->data);
	}
    }
  return root;

}

void inorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  inorder_traversal (root->left);

  cout << root->data << " "; inorder_traversal (root->right);

}

int main ()
{
  Tree *root = new Tree (15);
  root->left = new Tree (13);
  root->right = new Tree (18);
  root->left->left = new Tree (8);
  root->left->right = new Tree (14);
  root->right->left = new Tree (16);
  root->right->right = new Tree (19);
  
  cout << "Inorder Traversal of the Binary Search Tree:";
  inorder_traversal (root);
  cout << endl;
  
  cout << "Value to be deleted : 18 \n";
  Delete (root, 18);
  cout << "Inorder Traversal :";
  inorder_traversal (root);
  cout << endl;
}

Output:

Inorder Traversal of the Binary Search Tree:8 13 14 15 16 18 19 
Value to be deleted : 18 
Inorder Traversal :8 13 14 15 16 19

Explanation:

The Tree class is used to create nodes of a Binary Search Tree, where each node stores a value and pointers to its left and right child.
The Delete() function recursively searches for the node to be removed by comparing the given value with the current node and moving left or right based on BST rules.
If the node to be deleted has no child or only one child, the node is removed and its child (if any) is directly connected to its parent.
If the node has two children, the smallest value from the right subtree (inorder successor) is found, copied to the current node, and then deleted from its original position.
The inorder_traversal() function prints the tree in sorted order, helping verify the structure of the BST before and after deletion.

Time and Space Complexity:

Operation	Time Complexity	Space Complexity
BST Deletion	O(h)	O(h)
Searching Node	O(h)	O(h)
Finding Inorder Successor	O(h)	O(1)
Inorder Traversal	O(n)	O(h)

Conclusion:

Deletion in a Binary Search Tree is an important operation that removes a node while preserving the ordered structure of the tree. Depending on whether the node has no child, one child, or two children, different strategies are applied to maintain the BST properties.

By correctly handling all deletion cases and using the inorder successor when required, the tree remains balanced and searchable. The C++ implementation clearly demonstrates how deletion works and verifies the result using inorder traversal before and after the operation.

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java