Insertion In A Binary Search Tree In C++

February 2, 2026

Insertion In A Binary Search Tree

A Binary Search Tree (BST) is a hierarchical data structure in which each node contains a key value and at most two child nodes, commonly referred to as the left and right subtrees. The defining property of a BST is that all elements stored in the left subtree of a node are smaller than the value of the node itself, while all elements in the right subtree are greater. This ordered structure enables efficient searching, insertion, and deletion operations.

A binary search tree is a tree in which the data in left subtree is less than the root and the data in right subtree is greater than the root. In this article, insertion is performed using recursion in C++.

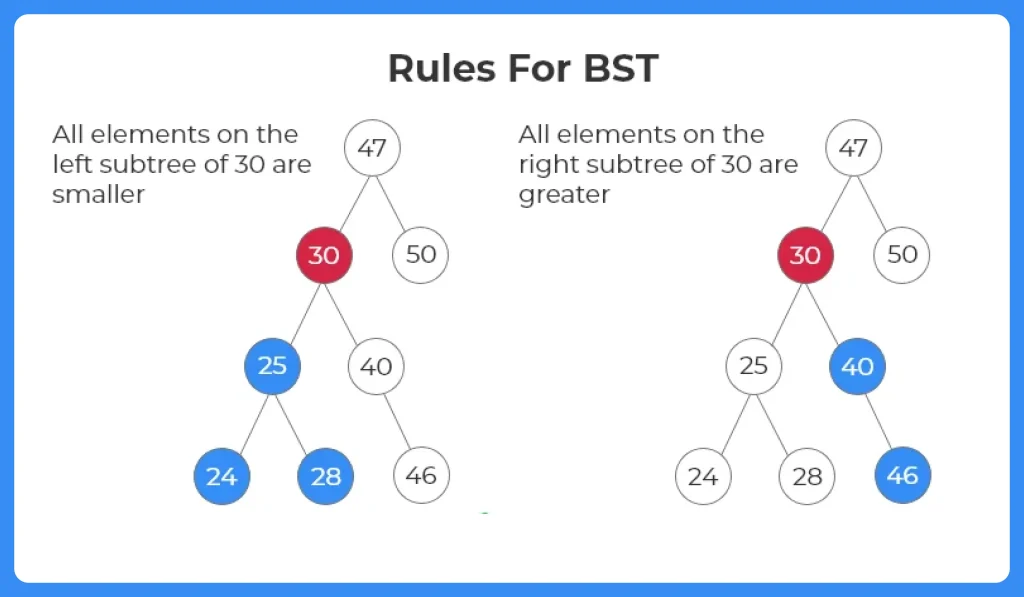
Rules For Binary Search Tree:

Left subtree for any given node will only contain nodes which are lesser than the current node
Right subtree for any given node will only contain nodes which are greater than the current node
This is valid for all nodes present in BST.

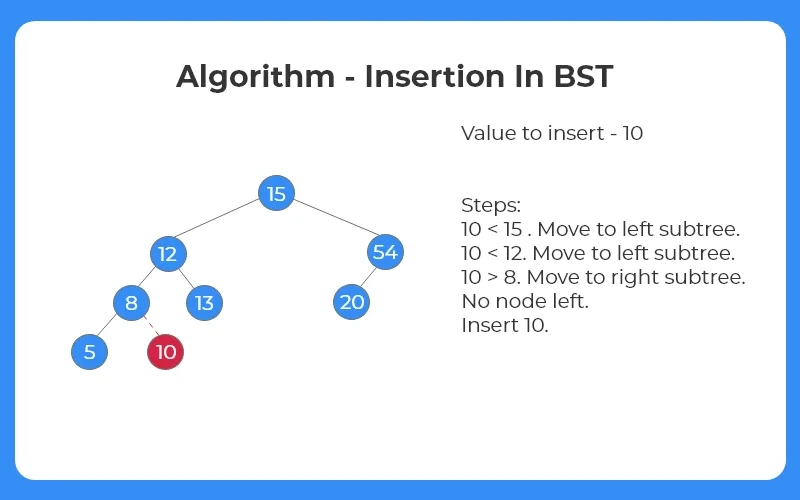
Algorithm To Insert In BST:

Input the value of the element to be inserted.
Start from the root.
If the input element is less than current node, recurse for left subtree otherwise for right subtree.
Insert the node wherever NULL is encountered.

Binary Search Trees in Data Structure(Introduction)

Introduction to Binary Search Tree

BST: Search in a Binary Search Tree

BST: Deletion in a Binary Search Tree

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Code Implementation for Insertion in a Binary Search Tree in C++

Run

#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
  int data;
  Tree *left = NULL, *right = NULL;
  // Constructor initialised
    Tree (int x)
  {
    data = x;
    left = NULL;
    right = NULL;
  }
};

Tree *insert_node (Tree * root, int x)
{

  if (root == NULL)
    {
      Tree *temp = new Tree (x);
      return temp;
    }

  if (root->data > x)
    {
      root->left = insert_node (root->left, x);
    }

  else
    {
      root->right = insert_node (root->right, x);
    }
  return root;

}

void inorder_traversal (Tree * root)
{
  if (root == NULL)
    return;
  inorder_traversal (root->left);

  cout << root->data << " "; inorder_traversal (root->right);

}

int main ()
{
  Tree *root = new Tree (15);
  root->left = new Tree (13);
  root->right = new Tree (18);
  root->left->left = new Tree (8);
  root->left->right = new Tree (14);
  root->right->left = new Tree (16);
  root->right->right = new Tree (19);
  
  cout << "Inorder Traversal of the Binary Search Tree:";
  inorder_traversal (root);
  
  cout <

Output:

Inorder Traversal of the Binary Search Tree:8 13 14 15 16 18 19 
Value to be inserted : 17 
Inorder Traversal :8 13 14 15 16 17 18 19

Explanation:

Defines a Tree class to represent nodes of a Binary Search Tree.
Constructor initializes node data with left and right pointers as NULL.
insert_node() inserts elements recursively following BST rules.
inorder_traversal() prints nodes in sorted order for a BST.
main() manually creates a BST and displays its inorder traversal output.

Time and Space Complexity:

Operation	Time Complexity	Space Complexity
BST Node Insertion	O(h)	O(h)
Inorder Traversal	O(n)	O(h)
Tree Node Creation	O(1)	O(1)

Conclusion:

The BST insertion article explains how to add a new element into a Binary Search Tree while maintaining the BST property values in the left subtree are smaller and values in the right subtree are greater than the parent node. It uses a recursive approach where the tree is traversed until an empty spot is found, and the new node is inserted there.

Introduction to Trees

Binary Trees

Binary Tree in Data Structures (Introduction)
Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
Inorder Postorder PreOrder Traversals Examples
- Inorder Tree Traversal in Binary Tree: C | C++ | Java
- Preorder Tree Traversal in Binary Tree : C | C++ | Java
- Postorder Tree Traversal in Binary Tree : C | C++ | Java
Tree Traversal without Recursion
- Postorder Preorder Inorder Traversal without recursion
- Inorder Tree Traversal without Recursion – C | C++ | Java
- Preorder Tree Traversal without Recursion – C | C++ | Java
- Postorder Tree Traversal without Recursion – C | C++ | Java

Binary Search Trees

Binary search tree in Data Structures (Introduction)
- BST: Introduction to Binary Search Tree
- BST: Binary Search Tree Program : C | C++ | Java
- BST: Search a node in Binary Search Tree : C | C++ | Java
- BST: Insertion in a Binary Search Tree : C | C++ | Java
- BST: Deletion in a Binary Search Tree : C | C++ | Java

Traversals

Traversal in Trees
Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
Tree Traversals: Depth First Search (DFS) : C | C++ | Java
Construct a Binary Tree from Postorder and Inorder

B – Trees

B-Tree
- B-Tree: Introduction
- B-Tree: Insertion : C | C++ | Java
- B-Tree: Deletion : C | C++ | Java

AVL Trees

AVL Trees
- AVL Trees: Introduction
- AVL Tree Insertion : C | C++ | Java
- AVL Tree Deletion : C | C++ | Java
- Insertion in a Binary Tree (Level Order) – C | C++ | Java
- Searching in Binary Tree – C | C++ | Java
- Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

Depth First Traversals – C | C++ | Java
Level Order Traversal – C | C++ | Java
Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
Find size of the Binary tree – C | C++ | Java
Find the height of binary tree – C | C++ | Java
Find maximum in binary tree – C | C++ | Java
Check whether two tree are identical- C| C++| Java
Spiral Order traversal of Tree- C | C++| Java
Level Order Traversal Line by Line – C | C++| Java
Hand shaking lemma and some Impotant Tree Properties.
Check If binary tree if Foldable or not.- C| C++| Java
check whether tree is Symmetric – C| C++| Java.
Check for Children-Sum in Binary Tree- C|C++| Java
Sum of all nodes in Binary Tree- C | C++ | Java
Lowest Common Ancestor in Binary Tree- C | C++ | Java