Binary Search Tree Program in Java
Binary Search Tree Program
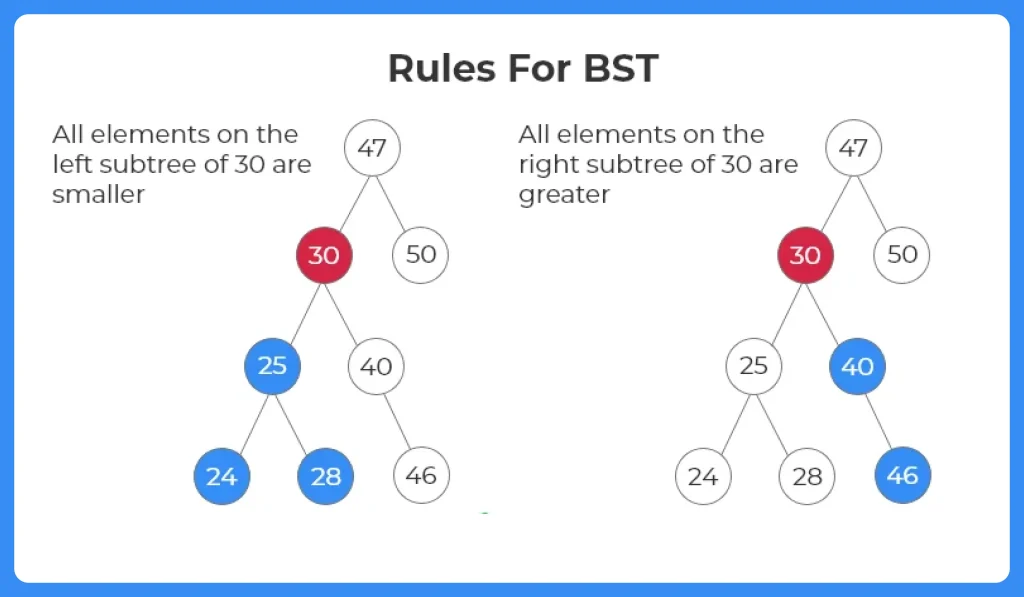
A binary search tree is a tree in which the data in left subtree is less than the root and the data in right subtree is greater than the root. In this article , we will cover all the basics of binary search tree program in java.

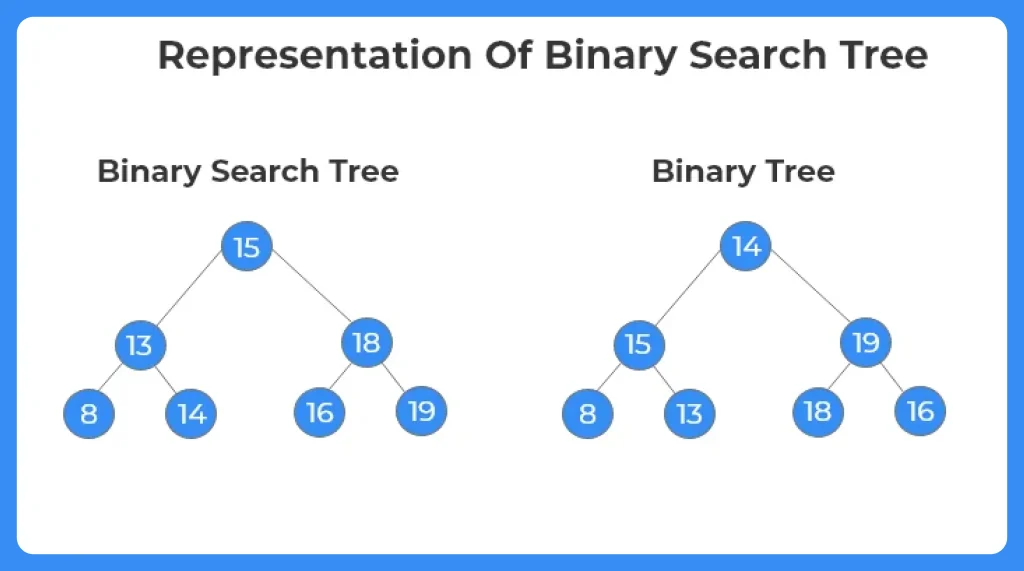
Reprsentation Of BST:
- The representation of a BST is similar to that of a binary tree. The order of a BST is ‘2’. Each node can have at most two children.
- Only difference between the two is that there is a certain criteria of arrangement or insertion of the elements based on their comparisons with the root node and the sub tree segment they are added to.
Operations In A BST:
- Traversal
- Searching
- Insertion
- Deletion
Features Of A BST:
- Fast look-up.
- Efficient addition and removal of items.
- Used to implement dynamic set of items
Code For Binary Search Tree
Run
// Binary Tree
import java.util.*;
/*Representing a Node of a binary tree */
class Node
{
int value;
Node left, right;
Node (int value)
{
this.value = value;
left = null;
right = null;
}
}
class BTS
{
Node root; //root of a binary search tree
BTS ()
{
root = null;
}
public void insert (int item)
{
root = insertNode (root, item); //calling inserNode() method
}
public Node insertNode (Node root, int item)
{
if (root == null) //if root is null create a new Node
{
root = new Node (item);
return root;
}
if (item < root.value) //if item is less than the current value then traverse left subtree
root.left = insertNode (root.left, item);
else if (item > root.value) //if item is greater than the cureent value then traverse the right subtree
root.right = insertNode (root.right, item);
return root;
}
public void delete (int value)
{
root = deleteNode (root, value); //calling deleteNode() method
}
public Node deleteNode (Node ptr, int value)
{
if (ptr == null)
return ptr;
if (value < ptr.value) //if value is less than current value
ptr.left = deleteNode (ptr.left, value);
else if (value > ptr.value) //if value if greater than current value
ptr.right = deleteNode (ptr.right, value);
else
{
//if node having max one child
if (ptr.left == null)
return ptr.right;
else if (ptr.right == null)
return ptr.left;
// if node having two children then get the inorder predecessor of node
ptr.value = minimumValue (ptr.left);
//delete the inorder predecessor
ptr.left = deleteNode (ptr.left, ptr.value);
}
return ptr;
}
//get minimum element in binary search tree
public int minimumValue (Node ptr)
{
int min;
for (min = ptr.value; ptr.right != null; ptr = ptr.right)
min = ptr.right.value;
return min;
}
public Node searchNode (Node root, int value)
{
if (root == null)
return null;
if (root.value == value) // return true if value is found in binary tree
return root;
else if (value < root.value)
return searchNode (root.left, value); //traverse left subtree
else
return searchNode (root.right, value); //traverse right subtree
}
public void print (Node ptr)
{
if (ptr == null)
return;
print (ptr.left);
System.out.print (ptr.value + " ");
print (ptr.right);
}
}
public class Main
{
public static void main (String[]args)
{
//Adding Nodes to the binary tree
BTS tree = new BTS ();
tree.insert (15);
tree.insert (19);
tree.insert (10);
tree.insert (13);
tree.print (tree.root);
System.out.println ();
tree.delete (15);
tree.print (tree.root);
System.out.println ();
//calling search function if element is found then it will return true else return false
Node node = tree.searchNode (tree.root, 13);
if (node != null)
System.out.println ("Element " + node.value +
" is found in binary tree");
else
System.out.println ("Element is not found in binary tree");
}
}
Output :
20 30 40 50 60 70 80
Advantages Of BST:
- Inorder Traversal gives sorted order of elements.
- Easy to implement order statistics.
- Helpful in range queries.
Disadvantages Of BST:
- The cost of operations may be high.
- Shape of tree depends on insetions and may be degenerated.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java





