Spiral order Traversal of Binary Tree code in c++.
Spiral Order Tree Traversal
A binary tree is said to be identical with another binary tree if both the trees have the same data and also the same arrangement of the data.In this article, we will learn the approach and code to check whether 2 binary trees are identical or not.

Spiral Trees
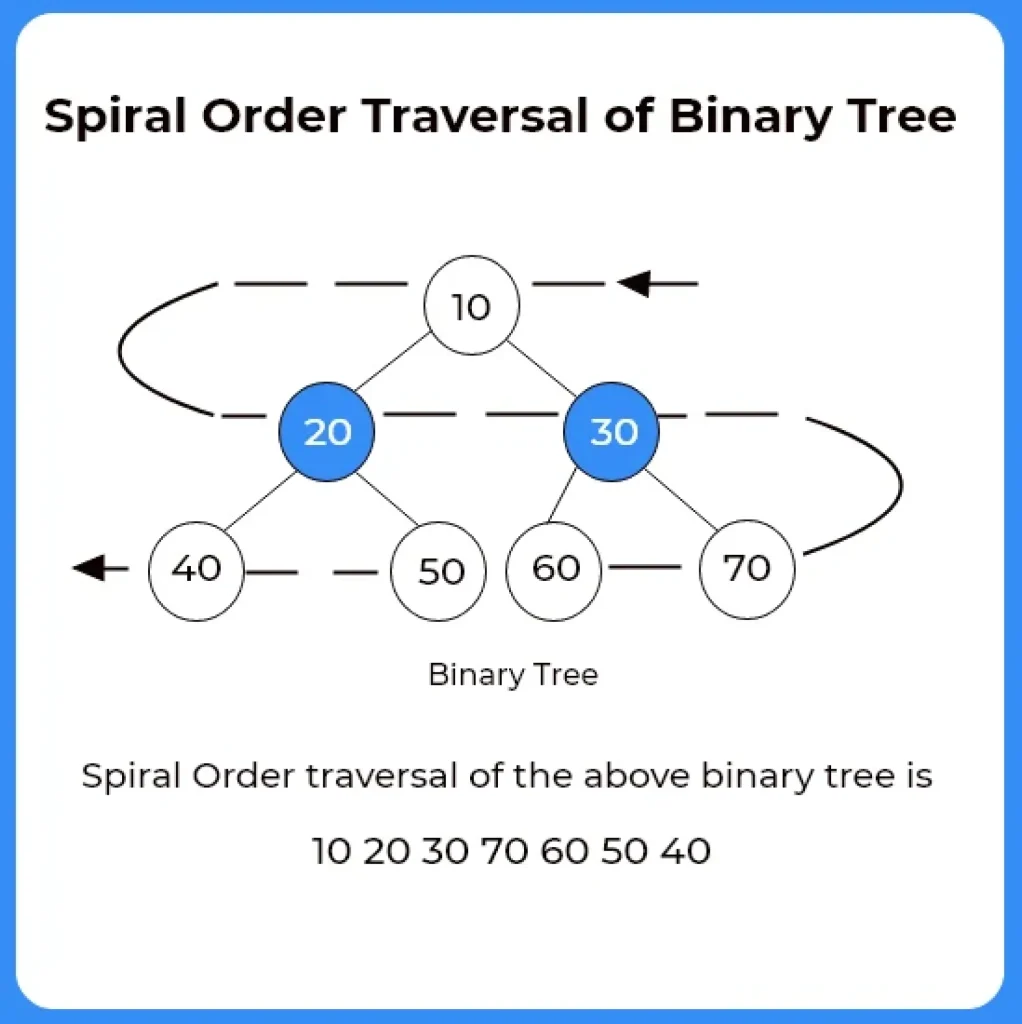
Given a Tree and we need to print the spiral order traversal of the given tree.
By spiral Order Traversal We mean that alternate levels should be printed in alternate order .
For eg:- Level 0 to be printed left to right
Level 1 from right to left. and so on
The observation one can make is that if level is odd we are printing the nodes left to right and if it is even we are printing them right to left.
Thus idea to be used is similar to what we do in level order traversal and additionally we need to maintain a counter which maintain level numbers so that printing can be done accordingly
Thus we maintain two stacks and one stack is used for printing left to right while other is used for printing right to left.
Time complexity for this program is O(n) and same is also the space complexity.
Code Implementation for spiral order tree traversal in C++
#include<bits/stdc++.h>
using namespace std;
struct Node
{
int key;
Node *left, *right;
Node (int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
bool printLevelLeftToRight (Node * root, int level)
{
if (root == nullptr)
{
return false;
}
if (level == 1)
{
cout << root->key << " ";
return true;
}
bool left = printLevelLeftToRight (root->left, level - 1);
bool right = printLevelLeftToRight (root->right, level - 1);
return left || right;
}
bool printLevelRightToLeft (Node * root, int level)
{
if (root == nullptr)
{
return false;
}
if (level == 1)
{
cout << root->key << " ";
return true;
}
bool right = printLevelRightToLeft (root->right, level - 1);
bool left = printLevelRightToLeft (root->left, level - 1);
return right || left;
}
void spiralOrderTraversal (Node * root)
{
if (root == nullptr)
{
return;
}
int level = 1;
while (printLevelLeftToRight (root, level++) &&
printLevelRightToLeft (root, level++));
}
int main ()
{
Node *root = new Node (15);
root->left = new Node (10);
root->right = new Node (20);
root->left->left = new Node (8);
root->left->right = new Node (12);
root->right->left = new Node (16);
root->right->right = new Node (25);
spiralOrderTraversal (root);
return 0;
}
Output: 15 20 10 8 12 16 25
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others






Login/Signup to comment