Size of sub-array with Max Sum in Java

May 2, 2023

Size of sub-array with Max Sum in Java

Here, in this page we will discuss the program to find size of sub-array with max sum in Java. We use Kadane’s algorithm, which runs in O(n) time.
The idea is to keep scanning through the array and calculating the maximum sub-array that ends at every position. If current sum becomes 0 then at that point we also update the starting index.

size of subarray with max sum

Size of sub-array with Max Sum in Java

The “Size of Sub-array with Maximum Sum” problem is a common algorithmic problem that involves finding the length or size of a contiguous sub-array within an array of integers, such that the sum of the sub-array is maximum among all possible sub-arrays. In other words, we need to find the sub-array with the largest sum.

Here’s an example to illustrate the problem:

Given an array of integers: [-2, 1, -3, 4, -1, 2, 1, -5, 4]

The subarray with the maximum sum is [4,-1,2,1], and the sum of this sub-array is 6. Thus, the size of the subarray with the maximum sum is 4.

The problem can be solved using efficient algorithms such as Kadane’s algorithm, which has a time complexity of O(N), where N is the size of the input array. Kadane’s algorithm iterates through the array in a single pass, keeping track of the maximum sum of sub-arrays ending at each position of the array, and updating it as necessary.

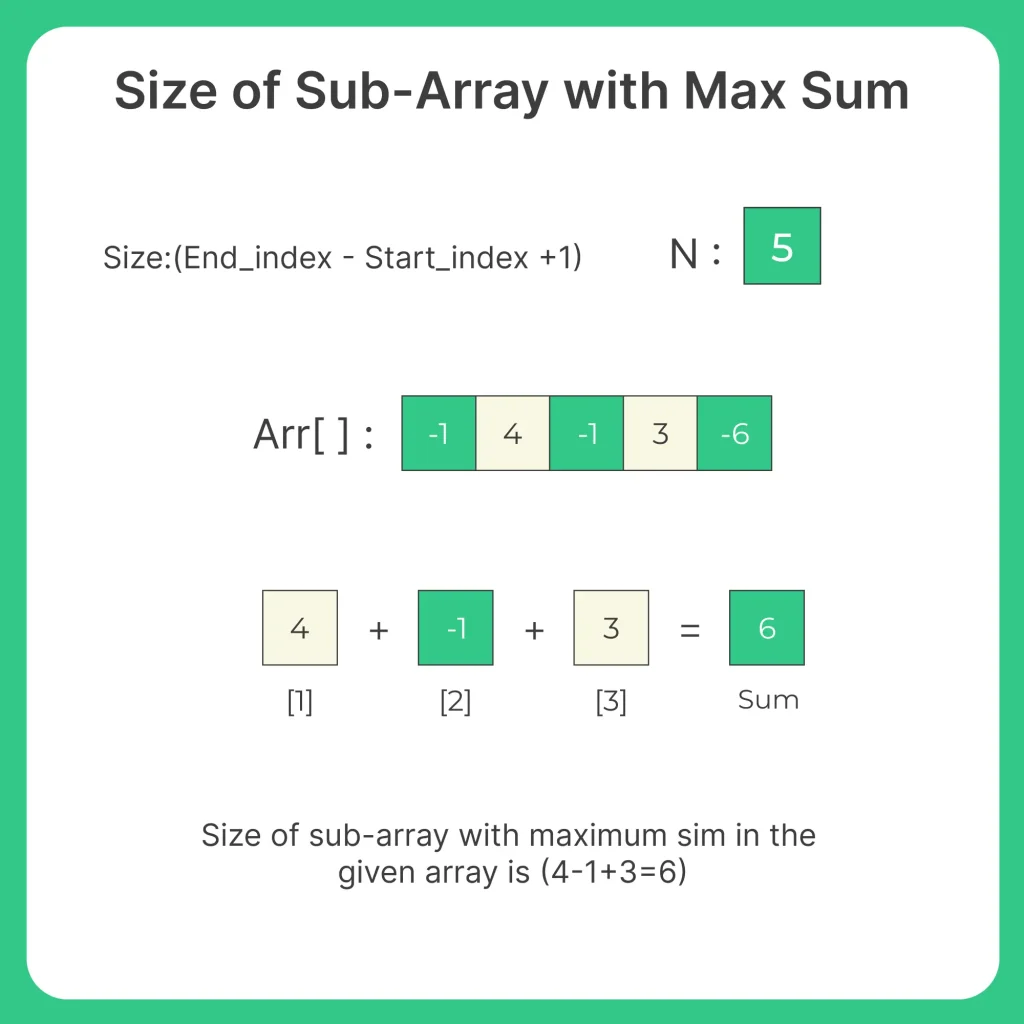
Size of sub-array with max sum in Java
DSA desktop gif
DSA mobile gif

Given an array which consists of only 0, 1 and 2

Move all the negative elements to one side of the array

Find the Union and Intersection of the two sorted arrays

Find Largest sum contiguous Subarray

Minimize the maximum difference between heights 

Algorithm:

  1. Initialize max_sum to the smallest possible integer value, current_sum to 0, start to 0, and end to 0.

  2. Iterate through the array from left to right, for each element: a. Compare the current sum current_sum plus the current element with the current element itself. If the former is greater, update current_sum to the sum, and update end to the current index. b. If the current element is greater, start a new sub-array with the current element as the starting element, update current_sum to the current element, and update both start and end to the current index.

  3. Update max_sum if the current sum current_sum is greater.

  4. After the iteration, the sub-array with the maximum sum is indicated by the start and end indices, and the size of the sub-array is end - start + 1. Return this value as the result.

Java code for Size of sub-array with max sum

Run 
import java.util.*;

public class Main {
    public static void main(String[] args) {
        int[] arr = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
        int max_size = maxSizeSubarrayWithMaxSum(arr);
        System.out.println("Size of subarray with maximum sum: " + max_size);
    }

    public static int maxSizeSubarrayWithMaxSum(int[] nums) {
        int max_sum = Integer.MIN_VALUE;
        int current_sum = 0; // Initialize current_sum to 0
        int start = 0; // Initialize start index to 0
        int end = 0; // Initialize end index to 0

        for (int i = 0; i < nums.length; i++) {
            if (current_sum + nums[i] < nums[i]) {
                current_sum = nums[i];
                start = i;
            }
            else
            {
                current_sum += nums[i];
            }

            // Update max_sum if current_sum is greater
            if (current_sum > max_sum)
            {
                max_sum = current_sum;
                end = i;
            }
        }

        // Size of subarray with max sum is end - start + 1
        return end - start + 1;
    }
}

Output

Size of subarray with maximum sum: 4

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java