Maximum Average Sub-array of K length in Java
Maximum Average Sub-array of K length in Java
On this page we will discuss about Maximum Average sub-array of k length in Java language . We have to Find out the maximum possible average value of sub-array of K length from given sequence of N integers, a[1], a[2], , , , a[N] of N length and a integer K integer.
Maximum Average Sub-array of K length in Java
In Java, maximum average subarray of k length pertains to a contiguous sub-array of length k in a given array of numbers, where the average (mean) of the k elements is the highest among all possible sub-arrays of length k in that array. In simpler words, it refers to the sub-array of k consecutive elements whose sum is the largest possible among all sub-arrays of k consecutive elements in the array, resulting in the highest average value.
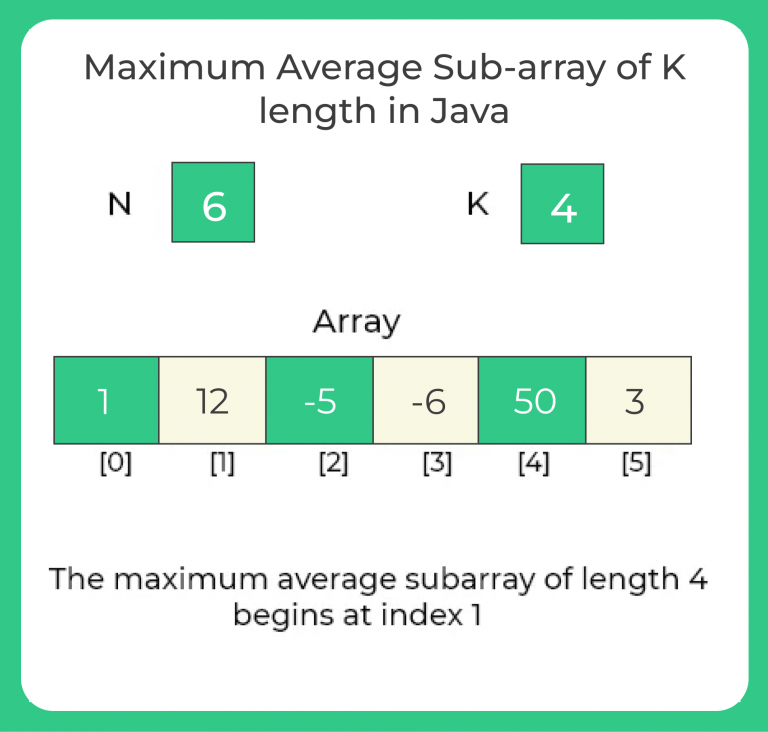
For example,consider the array
[1, 12, -5, -6, 50, 3] and k=4.
The subarrays of length 4 are [1, 12, -5, -6], [12, -5, -6, 50], [-5, -6, 50, 3], and their averages are 0.5, 12.75, and 10.5 respectively. The maximum average subarray of length 4 in this case is [12, -5, -6, 50], whose average is 12.75.
Algorithm:
Initialize
max_sumwith the sum of the firstkelements ofarrandmax_endwithk-1, which represent the sum and ending index of the first subarray of lengthk.Loop through the input array
arrfrom indexkton-1and for each indexi, compute the sum of the subarray of lengthkending at indexi, i.e.,curr_sum = sum of elements from arr[i-k+1] to arr[i].Compare
curr_sumwithmax_sum. Ifcurr_sumis greater thanmax_sum, updatemax_sumwithcurr_sumand updatemax_endwith the current indexi.After the loop,
max_endwill represent the ending index of the maximum average subarray of lengthk.Return the starting index of the maximum average subarray of length
kasmax_end - k + 1.
Java code for maximum average sub-array of k length
import java.util.Arrays;
public class Main {
// Returns beginning index of maximum average
// subarray of length 'k'
static int findMaxAverage(int[] arr, int n, int k) {
// Check if 'k' is valid
if (k > n) {
return -1;
}
// Create and fill array to store cumulative
// sum. csum[i] stores sum of arr[0] to arr[i]
int[] csum = new int[n];
csum[0] = arr[0];
for (int i = 1; i < n; i++) {
csum[i] = csum[i - 1] + arr[i];
}
int max_sum = csum[k - 1], max_end = k - 1;
for (int i = k; i < n; i++) { int curr_sum = csum[i] - csum[i - k]; if (curr_sum > max_sum) {
max_sum = curr_sum;
max_end = i;
}
}
// Return starting index
return max_end - k + 1;
}
// Driver program
public static void main(String[] args) {
int[] arr = {-1, 10, -15, -6, 50, 3};
int k = 4;
int n = arr.length;
System.out.println("The maximum average subarray of length " + k + " begins at index " + findMaxAverage(arr, n, k));
}
}
Output
The maximum average subarray of length 4 begins at index 1
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java






Login/Signup to comment