Find size of the Binary tree
Size of the Binary Tree
Size of Binary tree is defined as the number of nodes in the given tree. It can be easily calculated using recursion and tree traversals. In this article this problem is solved using recursion.

Find size of the Binary Tree
Algorithm
Size of the binary tree can be easily calculated using recursion.
Size of tree= Size of left subtree + Size of right subtree + 1 ( For the node itself ).
Now the left and right subtree size can be calculated with the help of recursion.
Example
Size of a binary tree is the number of nodes present in it.
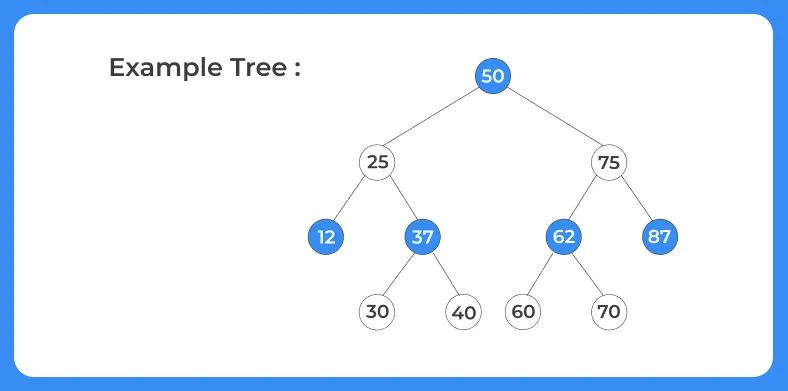
For this tree, size is 11. It is obtained with the help of recursion. Each subtree gives its size and at last we get the sizeof the complete tree. It is explained as:
- size(50) is called initially. It calls size(25) and size(75)
- size(25) calls size(12) and size(37)
- size(12) returns 1 and size(37) calls size(30) (returns 1) and size(40) (returns 1). So size(37) returns 1 + 1 + 1 = 3
- Now size(25) returns 1 + 3 + 1 =5. This is size of left subtree of 50
- In the similar way, we get size of right subtree of 50. The max would be 5.
- Now size of the tree would be- left subtree size (5) + right subtree size (5) + 1 (for the root node) = 11.
- Hence size of the tree is 11.

Java Program to Construct Tree from given Postorder and Preorder Traversals
import java.util.*;
public class Main
{
// Binary tree class
public static class BinaryTree
{
// Node class
public class Node
{
int data;
Node left;
Node right;
public Node (int data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
private Node root;
public BinaryTree (int[]pre, int[]post)
{
this.root =
this.construct (pre, 0, pre.length - 1, post, 0, post.length - 1);
}
private Node construct (int[]pre, int presi, int preei, int[]post,int postsi, int postei)
{
// this case occurs when a node has only one child
if (presi > preei)
{
return null;
}
Node node = new Node (pre[presi]);
node.left = null;
node.right = null;
if (presi == preei)
{
return node;
}
//Searching pre[presi + 1] in postorder array
int pos = -1;
for (int i = postsi; i <= postei; i++)
{
if (post[i] == pre[presi + 1])
{
pos = i;
break;
}
}
//Number of elements in left subtree
int clc = pos - postsi + 1;
//Left subtree
node.left =
this.construct (pre, presi + 1, presi + clc, post, postsi, pos);
//Right subtree
node.right =
this.construct (pre, presi + clc + 1, preei, post, pos + 1,postei - 1);
return node;
}
public int size ()
{
return this.size (this.root);
}
//Function to find size of tree
private int size (Node node)
{
//Base case
if (node == null)
{
return 0;
}
//Calculate left subtree size
int lsize = this.size (node.left);
//Calculate right subtree size
int rsize = this.size (node.right);
//Size of tree is left subtree size + right subtree size + 1 (for root node)
return lsize + rsize + 1;
}
}
public static void main (String[]args) throws Exception
{
// Construct binary tree
int[] pre = { 50, 25, 12, 37, 30, 40, 75, 62, 60, 70, 87 };
int[] post = { 12, 30, 40, 37, 25, 60, 70, 62, 87, 75, 50 };
BinaryTree bt = new BinaryTree (pre, post);
System.out.println ("Size of the Tree is : " + bt.size ());
}
}
Output:
Size of the Tree is : 11
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java





