Maximum Average Subarray of K length in Java
Java Program for Maximum Average Sub Array of K Length
Finding the Maximum Average Subarray of K length in Java is a classic array problem that helps programmers understand how to efficiently work with sliding windows, array traversal, and time optimization. This problem is frequently asked in coding interviews and helps test a candidate’s ability to think logically about optimizing repetitive calculations.
In this article, we will explore what this problem is, why it is important, and how to solve it using both brute force and optimized approaches, including complete Java code, step by step logic, and complexity analysis.

Maximum Average Sub Array of K length in Java
What is the Problem?
Given an integer array arr[] and an integer k, your task is to find the maximum average of all contiguous subarrays of size k.
In simple terms:
- You have an array.
- You have to pick continuous k elements.
- Compute their average.
- Among all possible subarrays of length k, find the one that gives the maximum average value.
Example:
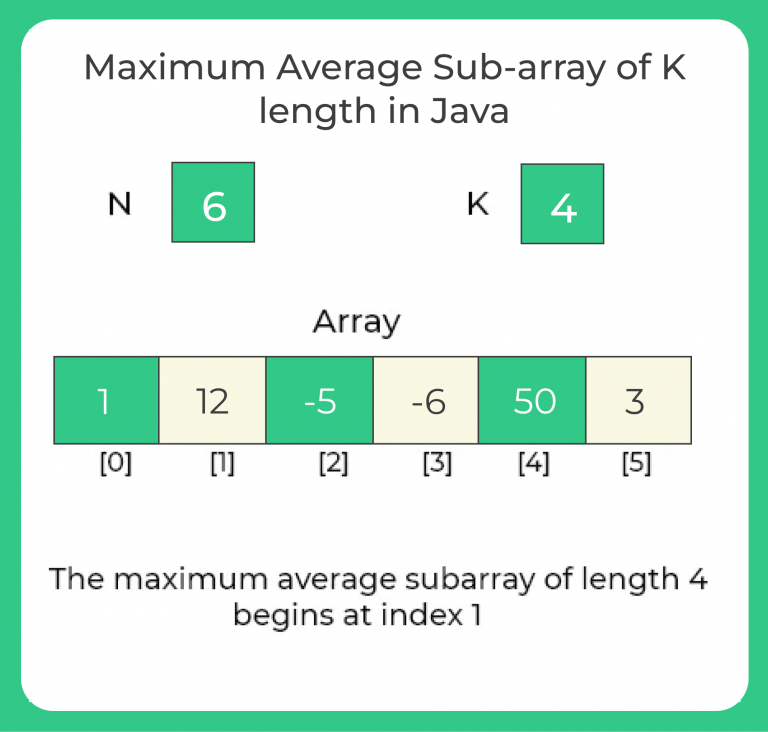
Input: arr = [1, 12, -5, -6, 50, 3], k = 4 Output: 12.75 Explanation: Subarrays of size 4 are: [1, 12, -5, -6] → Average = 0.5 [12, -5, -6, 50] → Average = 12.75 [-5, -6, 50, 3] → Average = 10.5 Maximum average = 12.75
If each element in the array represents a student's marks in a series of tests, finding the maximum average subarray of k tests helps you determine during which continuous k exams the student performed best on average.
Different Methods for Maximum Average Sub Array of K length
There are 2 main ways to solve this problem:
Learn DSA
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
1. Brute Force Approach for Maximum Average Sub Array of K length
In this approach, we calculate the sum (and average) of every possible contiguous subarray of size k using nested loops. Then, we keep track of the maximum average found so far.
Algorithm:
- Initialize a variable maxAvg to a very small number.
- Use a loop to pick every possible starting index i of a subarray.
- For each starting point, calculate the sum of the next k elements.
- Compute the average of this subarray.
- Compare and update maxAvg if a higher average is found.
- Finally, print the maximum average.
Code:
public class MaxAverageSubarray {
public static double findMaxAverageBruteForce(int[] arr, int k) {
int n = arr.length;
double maxAvg = Double.NEGATIVE_INFINITY;
for (int i = 0; i <= n - k; i++) {
int sum = 0;
for (int j = i; j < i + k; j++) {
sum += arr[j];
}
double avg = (double) sum / k;
if (avg > maxAvg) {
maxAvg = avg;
}
}
return maxAvg;
}
public static void main(String[] args) {
int[] arr = {1, 12, -5, -6, 50, 3};
int k = 4;
System.out.println("Maximum average subarray of length " + k + " is: " + findMaxAverageBruteForce(arr, k));
}
}
Input:
Array: [1, 12, -5, -6, 50, 3] k = 4
Output:
Maximum average subarray of length 4 is: 12.75
Space Complexity: O(1)
2. Optimized Approach for Maximum Average Sub Array of K length
In the brute force method, we re calculate the sum for every window which is inefficient. To improve, we can use the sliding window approach where we reuse the previous sum.
Instead of recomputing the sum of each window from scratch, we just:
- Subtract the element that is leaving the window.
- Add the new element that is entering the window.
This drastically reduces the number of operations.
Step By Step Explanation:
Let’s take the same example:
arr = [1, 12, -5, -6, 50, 3], k = 4
Step 1: Calculate the sum of the first window (first 4 elements).
- → sum = 1 + 12 + (-5) + (-6) = 2
- → maxSum = 2
Step 2: Slide the window by one element at a time:
- Subtract the first element of the previous window.
- Add the next element of the new window.
Window 2: Subtract 1, add 50 → new sum = 2 – 1 + 50 = 51
→ maxSum = 51
Window 3: Subtract 12, add 3 → new sum = 51 – 12 + 3 = 42
→ maxSum = 51 (unchanged)
Step 3: Compute maximum average → maxSum / k = 51 / 4 = 12.75
Code:
public class MaxAverageSubarrayOptimized {
public static double findMaxAverage(int[] arr, int k) {
int n = arr.length;
// Step 1: Compute initial window sum
double windowSum = 0;
for (int i = 0; i < k; i++) {
windowSum += arr[i];
}
double maxSum = windowSum;
// Step 2: Slide the window
for (int i = k; i < n; i++) {
windowSum += arr[i] - arr[i - k];
if (windowSum > maxSum) {
maxSum = windowSum;
}
}
// Step 3: Return maximum average
return maxSum / k;
}
public static void main(String[] args) {
int[] arr = {1, 12, -5, -6, 50, 3};
int k = 4;
System.out.println("Maximum average subarray of length " + k + " is: " + findMaxAverage(arr, k));
}
}
Input:
Array: [1, 12, -5, -6, 50, 3] k = 4
Output:
Maximum average subarray of length 4 is: 12.75
Space Complexity: O(1)
Comparison Between Both Methods
| Approach | Technique | Time Complexity | Space Complexity | Efficiency |
|---|---|---|---|---|
| Brute Force | Nested loops | O(n * k) | O(1) | Slow for large arrays |
| Sliding Window | Reusing previous window sum | O(n) | O(1) | Very efficient |
Maximum Average Subarray of K length in Java problem teaches an essential concept in algorithmic optimization, the sliding window technique.
- While the brute force approach helps understand the problem, the sliding window method makes the solution more efficient and suitable for real world applications.
- By mastering this concept, you will be better prepared to solve many similar array based problems that involve continuous segments and sum or average calculations efficiently.
FAQ's related to Maximum Average Sub Array of K length
Answer:
It’s the largest possible average value among all contiguous subarrays of size k in a given integer array.
Answer:
Use the sliding window approach, where you compute the sum of the first window and then adjust it by subtracting the element leaving the window and adding the new element entering it.
Answer:
The optimized solution using the sliding window technique runs in O(n) time and uses O(1) extra space.
Answer:
Yes. The logic works the same way regardless of whether the elements are positive or negative.
Answer:
Yes. It’s commonly used in problems involving subarrays, substrings, or continuous ranges, such as maximum sum subarray, longest substring without repeating characters, and similar challenges.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others







Login/Signup to comment