Two Dimensional Arrays in C++
Introduction to Two Dimensional Arrays in C++
When working with data like grids, tables, or matrices in C++, two-dimensional arrays in C++(2D arrays) become incredibly useful. They allow you to store data in a structured format using rows and columns, just like a spreadsheet. This blog will describe you through everything you need to know about 2D arrays in C++, from basic initialization to performing operations like matrix addition.
The 2D array is organized as matrices which can be represented as the collection of rows and columns.

What is Two Dimensional Arrays in C++?
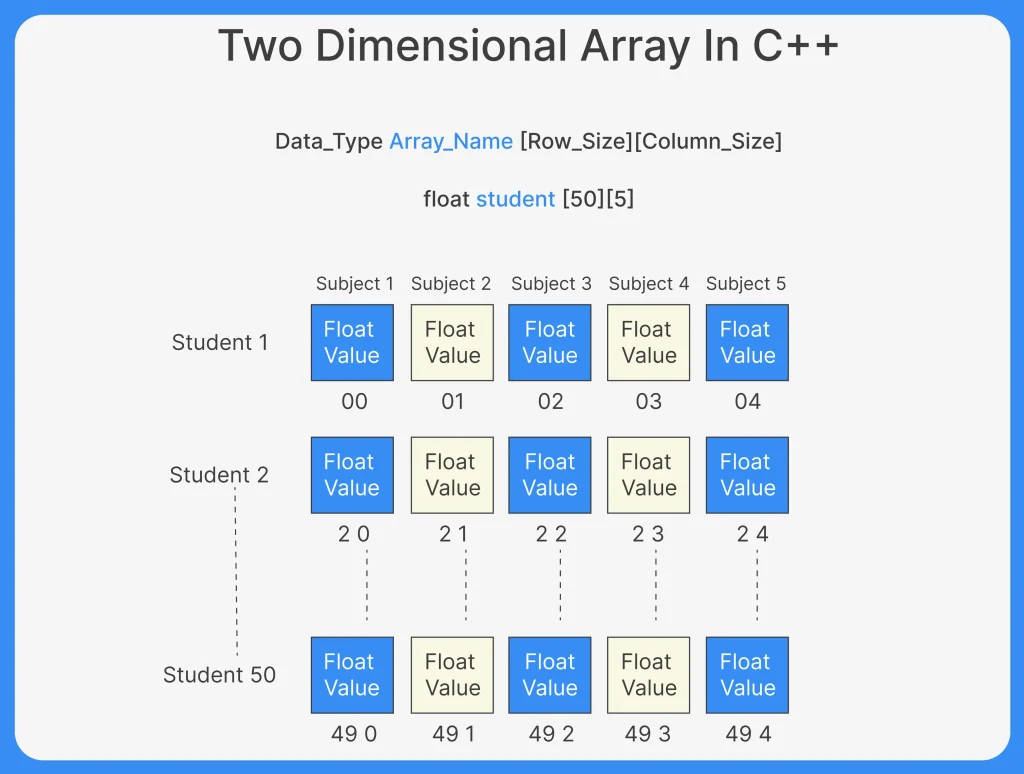
A two-dimensional array in C++ is an array of arrays. In simple words, it’s a way to store data in rows and columns format. It’s perfect when you need to represent a table, matrix, or grid.
- The elements of 2D arrays can be randomly accessed. Similar to one-dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells.
- There are two indices attached to a particular cell, one is its row number while the other is its column number.
Syntax :
The syntax of declaring a two-dimensional array is very much similar to that of a one-dimensional array, given as follows.
datatype arrayName[rows][columns];
Example:
int marks[3][4];

How to Initialize a 2D Array
Size of 2-D array
The total number of elements that can be stored in a multidimensional array can be calculated by multiplying the size of all the dimensions.
Example: The array int a[5][6] can store total (5*6) = 30 elements.
Initializing 2D Arrays
DIRECT METHOD
data_type[ ][ ] variable_name = { {R1C1, R1C2, ….}, {R2C1,R2C2, ….} };
Example: int [ ][ ] arr = { { 2 , 4 } , {6, 8 } };
USING LOOPS
We can use loops for initializing 2d array like
for (int i = 0; i < 2; i++) { for (int j = 0; j < 2; j++) { int a = x[i][j]; } }
You can fill in the values of a 2D array either at the time of declaration or later during program execution. To initialize a 2D Array, we mainly use three different way –
1. Full Initialization
2. Partial Initialization
3. Inline Initialization
1. Full Initialization
int matrix[2][3] = {
{1, 2, 3},
{4, 5, 6}
};This creates a 2-row and 3-column array.
2. Partial Initialization
int matrix[2][3] = {
{1},
{4, 5}
};Here, the missing values will be automatically filled with 0.
3. Inline Initialization
int matrix[][3] = { {1, 2, 3}, {4, 5, 6} };You can skip the row size if column size is mentioned.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
How to Print a 2D Array in C++
To print all elements of a 2D array, we use nested loops – one loop for rows and another for columns.
Example:
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 3; j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}This will display the 2D array in matrix form.
How to Take 2D Array Input from User
We can ask the user to enter elements of the array using cin.
Example: Taking 3×3 matrix input
int arr[3][3];
cout << "Enter elements of 3x3 matrix: " << endl;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cin >> arr[i][j];
}
}This helps the program accept dynamic input from users instead of fixed values.
Matrix Addition using Two Dimensional Array in C++
Matrix addition is a common operation where you add corresponding elements of two matrices.
Example:
int A[2][2] = {{1, 2}, {3, 4}};
int B[2][2] = {{5, 6}, {7, 8}};
int result[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
result[i][j] = A[i][j] + B[i][j];
}
}Output:
6 8 10 12
Pointer to a 2D Array in C++
You can also use pointers to access a 2D array. This helps in memory-level access and efficient programming.
Example:
int arr[2][2] = {{1, 2}, {3, 4}};
int (*ptr)[2] = arr;
cout << *(*(ptr + 1) + 1); // Output: 4Here, ptr points to the first row, and pointer arithmetic helps access any element in the array.
Passing 2D Array to a Function in C++
To use a 2D array inside a function (for display, calculation, etc.), you must pass it properly with the number of columns mentioned.
Example:
void display(int arr[][3], int rows) {
for (int i = 0; i < rows; i++) {
for (int j = 0; j < 3; j++) {
cout << arr[i][j] << " ";
}
cout << endl;
}
}Calling the Function:
int matrix[2][3] = {{10, 20, 30}, {40, 50, 60}};
display(matrix, 2);Conclusion
A two-dimensional array in C++ is a powerful way to organize data in rows and columns. Whether you’re working with student marks, matrices, or tables – 2D arrays make the job easier. By learning how to initialize, input, print, and pass them to functions, you are building the foundation for more complex applications like image processing, game development, and scientific computing.
FAQs
Static 2D arrays allocate memory contiguously in row-major order, where rows are stored sequentially. Dynamic 2D arrays (using pointers or new) may involve non-contiguous memory blocks, as each row is allocated separately. This affects pointer arithmetic and cache performance during traversal.
Three common approaches include specifying the column size explicitly (e.g., void func(int arr[], int rows)), using a pointer to an array (e.g., void func(int (*arr), int rows)), or passing a double pointer for dynamically allocated arrays (e.g., void func(int** arr, int rows, int cols)). The column size must be known for static arrays to ensure correct memory offset calculations.
Use nested new and delete[] operations:
int** arr = new int*[rows]; for(int i=0; i<rows; i++) arr[i] = new int[cols]; // Deallocation for(int i=0; i<rows; i++) delete[] arr[i]; delete[] arr;
Failing to deallocate any tier of memory causes leaks
Due to cache locality, row-major order favors row-wise traversal. For example:
for(int i=0; i<rows; i++)
for(int j=0; j<cols; j++)
arr[i][j];
Column-wise traversal jumps across memory blocks, leading to cache misses and slower execution.
Common pitfalls include incorrect initialization (e.g., mismatched row sizes in braces), out-of-bounds access, assuming dynamic arrays are contiguous, and type mismatches when passing arrays to functions. For example, treating int[][] as int** without proper casting can cause runtime errors.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java





Login/Signup to comment