Foldable Binary Tree
Check if a Tree is foldable or Not
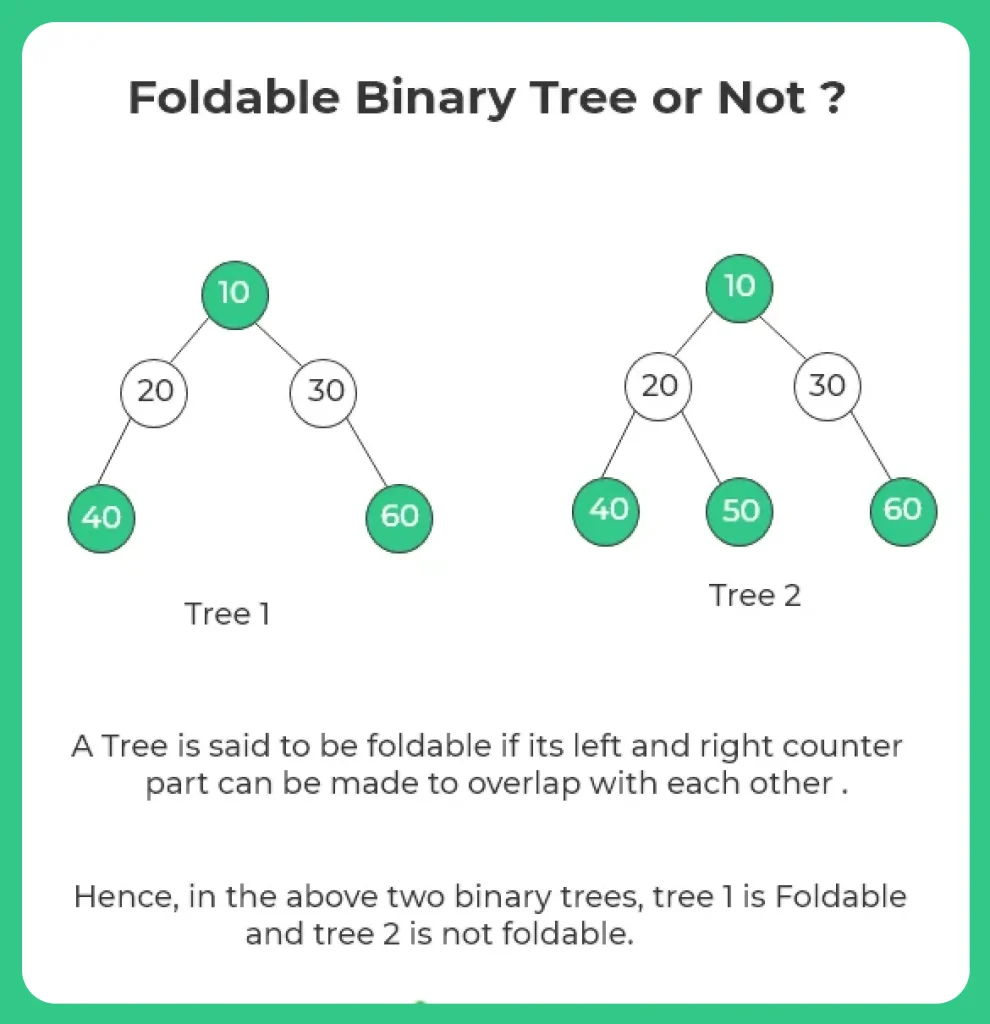
Here, in this page we will write a Java program to check whether the given binary tree is foldable or not. A Tree is said to be foldable if its left and right counter part can be made to overlap with each other .

Foldable Binary Tree
Algorithm :
- If tree is empty, then return true.
- Convert the left subtree to its mirror image mirror(root->left);
- Check if the structure of left subtree and right subtree is same and store the result. res = isStructSame(root->left, root->right);
- isStructSame() recursively compares structures of two subtrees and returns true if structures are same
- Revert the changes made in step 2 to get the original tree. mirror(root->left);
- Return result res stored in step 2.
Code in Java for Level Order Traversal Line by Line
Run
class Node {
int data;
Node left, right;
public Node(int item) {
data = item;
left = right = null;
}
public Node() {
data = 0;
left = right = null;
}
}
// Binary tree Class
class BTree {
static Node root;
static boolean isFoldableTree(Node node) {
if (node == null) {
return true;
}
return isFoldable(node.left, node.right);
}
static boolean isFoldable(Node nodeLeft, Node nodeRight) {
//Check both left and right node is null, if yes then that is fine, return true.
if (nodeLeft == null && nodeRight == null) {
return true;
}
//If one is present and other is null, return false.
if (nodeLeft == null || nodeRight == null) {
return false;
}
// The most Important step is -> when you are Checking if it is structurally a mirror image ,
// Send the left child of left subtree and right child of right subtree // together. Similarly,
// send the right child of left subtree and left child of right subtree.
boolean left = isFoldable(nodeLeft.left, nodeRight.right);
boolean right = isFoldable(nodeLeft.right, nodeRight.left);
return (left && right);
}
}
public class Main{
public static void main(String[] args) {
BTree tree = new BTree();
tree.root = new Node(1);
tree.root.left = new Node(5);
tree.root.right = new Node(4);
tree.root.left.left = new Node(9);
tree.root.left.right = new Node(7);
tree.root.right.left = new Node(10);
tree.root.right.right = new Node(13);
System.out.println(" The Given Tree is Foldable : " + tree.isFoldableTree(tree.root));
}
}
Output
The Given Tree is Foldable : true
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java





